辗转相除法求解二元一次不定方程
王晓英
(赤峰学院,内蒙古 赤峰 024000)
辗转相除法求解二元一次不定方程
王晓英
(赤峰学院,内蒙古 赤峰 024000)
本文旨在用辗转相除法求出二元一次不定方程的一个整数解,进而写出其一切整数解.
二元一次不定方程;整数解;辗转相除法
1 引言
二元一次不定方程的一般形式是

其中a,b,c是整数,a,b都不是0.首先讨论二元一次不定方程有整数解的条件.
定理1[1](1)式有整数解的充分必要条件是(a,b)|c.
证明 若(1)式有整数解,设为x0,y0,则ax0+by0=c,因为(a,b)|a,(a,b)|b,所以(a,b)|ax0+by0,即(a, b)|c.
反之,若(a,b)|c,则存在整数c1,使c=c1(a,b).又因为一定存在整数s,t,使as+bt=(a,b),所以有asc1+btc1=(a,b)c1=c.令x0=c1s,y0=c1t,即得ax0+by0=c,故(1)式有整数解x0,y0.
定理2[1]设(1)式有一整数解x0,y0;又设(a,b) =d,a=a1d,b=b1d,则(1)的一切解可以表示成

其中t=0,±1,±2,…….
由定理2可知,(1)式若有整数解,只需求出(1)式的一个特殊解即可写出一切解.
2 辗转相除法
定理3[1](带余数除法) 若a,b是两个整数,其中b>0,则存在着两个整数q及r,使得

成立,而且q及r是唯一的.
设a>0,b>0,由带余数除法可以得到:

上述计算方法叫作辗转相除法.其中rn=(a,b),并且不难得出辗转相除法中任一余数ri(i=1,2,…,n)与a,b的关系为:

其中P0=1,P1=q1,Pk=qkPk-1+Pk-2,
Q0=0,Q1=1,Qk=qkQk-1+Qk-2,k=2,3,…,n.
3 二元一次不定方程的解法
由定理1的证明看到,(1)式在有解的情况下,是先证明ax+by=(a,b)有解.因此要找出求出一个特殊解的方法,应该从这个方程着手,而这个方程的解与的解完全相同,并且.所以只需求出形如的一个特殊解.

由辗转相除法我们能求出|a|x+|b|y=1的一个特殊解,由此又很容易得出(3)式的一个解.因此,我们不妨假定(3)式中a>0,b>0.由(2)式可得出a[ (-1)n-1Qn]+b[(-1)nPn]=1,因此(3)式有一特殊解:x= (-1)n-1Qn,y=(-1)nPn.根据(2)式可以由下表更直观地给出求解Pn,Qn的过程:

由(3)式很容易得出ax+by=c的一个特殊解:

例1求107x+37y=25的一切整数解.
解(107,37)=1,1|25,故不定方程有解.

列下表求P3,Q3:

故107x+37y=1的特殊解是

107 x+37y=25的特殊解是

故107x+37y=25的一切整数解为:


或x=3-37t,y=-8+107t(t=0,±1,±2,……).
例2求111x-321y=75的一切整数解.
解(111,321)=3,3|75,故不定方程有解,且原方程的解与37x-107y=25的解完全相同.先解107x+37y=1,如例1,得出107x+37y=1的一个解:

易得37x-107y=1的一个解:

故37x-107y=25的一切解可表成:
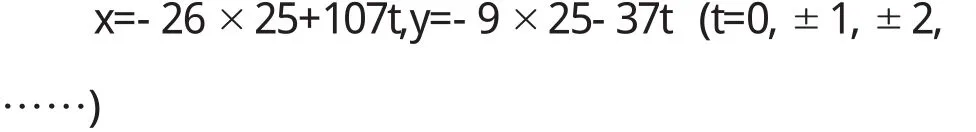
或x=-8+107t,y=-3+37t(t=0,±1,±2,……).
〔1〕闵嗣鹤,严士健.初等数论[M].北京:高等教育出版社,1998.
〔2〕胡学松,张勇宏,龚五星.二元一次不定方程整数解的通解公式[J].数学通讯,1995(6).
〔3〕朱志嘉,周定远.大系数二元一次不定方程解法探讨[J].数学通讯,1996(2).
O122.2
A
1673-260X(2014)12-0006-02

