基于Weibull分布的高速自润滑关节轴承可靠性分析

李彦伟，林晶，张令，赵颖春

(中国航空综合技术研究所，北京 100028)

高速自润滑关节轴承主要由内圈、外圈和自润滑衬垫3部分组成[1]，是一种可以实现高频摆动的自润滑关节轴承。自润滑关节轴承靠内圈与外圈内球面粘贴的自润滑衬垫的接触面滑动，所以磨损量是判定轴承寿命的主要依据。

由于高速自润滑关节轴承寿命服从Weibull分布，故可采用Weibull分布模型进行可靠性分析。Weibull分布模型参数的精度是轴承可靠性分析的关键，目前常用的参数估计法[2]中图估计法简单方便，但人为因素影响较大，所估计的参数精度较差；极大似然估计法获得的参数精度较高，但计算复杂繁琐；最佳线性无偏估计和最佳线性不变估计等方法都需借助专用表格，使用方便，但表格数量很大，且无表格之处无法使用；而最小二乘估计法能实现分布函数的线性化，是Weibull分布模型参数估计的一种较好方法。

试验数据是轴承可靠性分析的基础，但在试验过程中，经常出现试验磨损量未达到额定磨损量而试验中止的情况，产生了不完全试验数据。平均秩次法根据试验完成产生的完全试验数据和试验中止产生的不完全试验数据估计所有可能的秩次，求出平均秩次，代入近似中位秩公式，得到经验分布函数，充分利用试验数据的同时也取得了更加精确的参数估计值。下文采用结合平均秩次法的最小二乘参数估计法对高速自润滑关节轴承进行可靠性分析。

1 Weibull分布模型

Weibull分布模型[3]是近年来在轴承可靠性分析中使用最广泛的模型之一，Weibull分布的分布函数为

(1)

分布密度函数为

(2)

可靠度函数为

(3)

失效率函数为

(4)

式中：t为时间；η为尺度参数；β为形状参数。

2 参数估计

2.1 最小二乘参数估计

最小二乘估计是对线性函数中的未知参数进行估计，是Weibull分布模型参数估计的一种较好方法[4]。

将(1)式变形，得

(5)

两边取自然对数，得

lnln[1/(1-F(t))]=β(lnt-lnη)。

(6)

令

x=lnt，

(7)

y=lnln[1/(1-F(t))]，

(8)

A=β，

(9)

B=-βlnη，

(10)

则(6)式可转化为

y=Ax+B。

(11)

对于线性回归方程(11)式，回归系数A，B的最小二乘估计解为

(12)

(13)

在Weibull分布模型参数的最小二乘估计中，提高经验分布函数的精度即可求出一条偏差最小的回归直线和最符合实际的回归系数估计值。

2.2 平均秩次法

已有的经验分布函数计算方法是通过近似中位秩公式或直接查中位秩表[5]得到，误差较大。近似中位秩公式为

(14)

式中：i为完成试验的试件顺序号；n为试件数量；ti为第i个试件的试验时间。

平均秩次法是提高经验分布函数精度的一种有效方法，其原理是：根据完全试验数据和不完全试验数据估计出所有可能的秩次，再求出平均秩次,将平均秩次代入近似中位秩公式，求出其经验分布函数[6]。

文献[7]通过实践总结给出的计算平均秩的增量公式为

(15)

Ai=Ai-1+ΔAi，

(16)

式中：k为所有试件的排列顺序号，按试验完成时间和试验中止时间的大小排列；Ai为完成试验的试件的平均秩次；Ai-1为前一个完成试验试件的平均秩次。

将平均秩次Ai代入(14)式，得

(17)

将试验完成时间和通过计算得到的经验分布函数，利用最小二乘参数估计法，拟合出Weibull分布模型的回归直线，从而确定Weibull分布模型的尺度参数和形状参数。

3 可靠性分析

为了进行轴承可靠性分析，选择20套高速自润滑关节轴承进行磨损寿命试验。试验方法主要参照SAE(美国机动车工程师学会)标准AS 81819A，试验轴承在5.4 kN的径向载荷下进行高速摆动，摆动角度为±6°，摆动频率为20.78 Hz，当试验轴承的磨损量达到0.038 mm时，即可结束试验[8]。

通过记录20套轴承达到额定磨损量的时间和试验中止的时间，并按试验时间进行排序，结果见表1。表中包含了高速自润滑关节轴承磨损寿命试验的完全试验数据(C)和不完全试验数据(I)，去掉不完全试验数据，将轴承试验的完全试验数据进行排序，建立Weibull分布模型，采用平均秩次法，由(16)、(17)式分别计算平均秩次和经验分布函数，结果见表2。将计算结果(无量纲)按照最小二乘的原理拟合出最小二乘回归直线,如图1所示。

表1 高速自润滑关节轴承磨损寿命试验数据

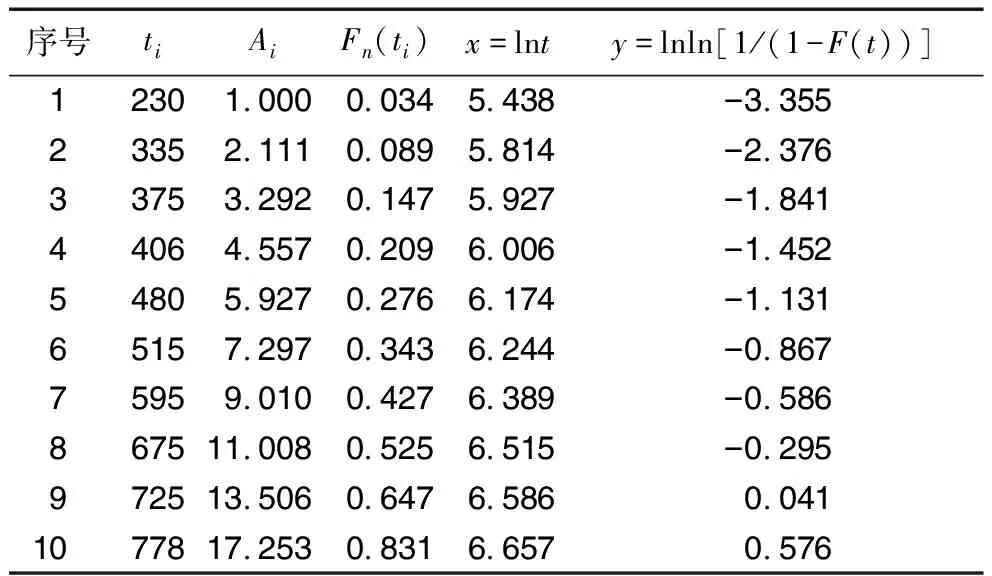
表2 平均秩次法计算的经验分布函数

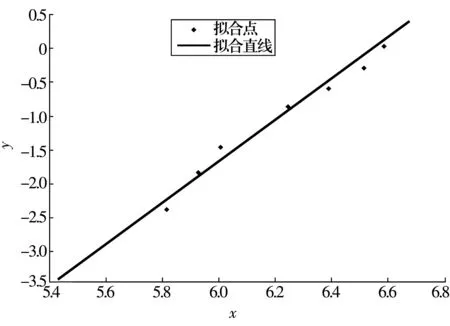
图1 平均秩次法的最小二乘拟合图

采用近似中位秩公式，由(10)式计算经验分布函数,结果见表3。将计算结果(无量纲)按照最小二乘的原理拟合出最小二乘回归直线,如图2所示。与图2相比，图1中的试验数据点在拟合直线两侧分布更均匀。S为最小二乘拟合度，其值越趋近于1则拟合越好。采用平均秩次法的计算结果经最小二乘拟合后S=0.985 7，采用近似中位秩公式的计算结果经最小二乘拟合后S=0.974 7，显然前者更加精确。

表3 近似中位秩公式计算的经验分布函数

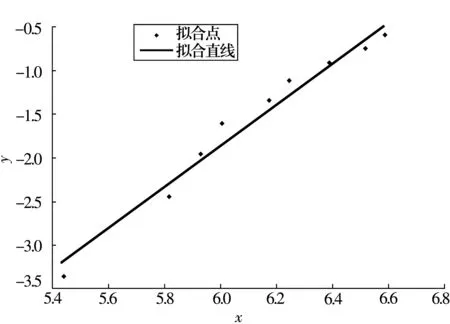
图2 近似中位秩公式的最小二乘拟合图

平均秩次法的直线拟合式为

lnln[1/(1-F(t))]=3.037lnt-19.88，

(18)

由(9)、(10)式解得β=3.037，η=696.404。

则分布函数为

(19)

分布密度函数为

(20)

可靠度函数为

(21)

失效率函数为

(22)

当R(t)=0.9时，由(21)式解得可靠度为90%的轴承寿命为t=332 h。

4 结束语

根据完全试验数据和不完全试验数据估计出所有可能的秩次,求出平均秩次,代入近似中位秩公式,得到轴承磨损寿命失效分布函数、分布密度函数、可靠度函数和失效率函数；进而计算出可靠度为90%的高速自润滑关节轴承的寿命。结合平均秩次法的最小二乘参数估计法拟合度高，拟合效果好，并能充分利用试验数据，得到的参数估计值更加精确。