基于DEA的地铁站拥挤踩踏风险分析

张立茂， 刘梦洁， 吴贤国， 仲景冰

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

基于DEA的地铁站拥挤踩踏风险分析

张立茂， 刘梦洁， 吴贤国， 仲景冰

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

由于运营时间短、客流量大、管理体系不健全等原因，国内地铁运营过程中存在诸多安全隐患，因拥挤造成踩踏事故的安全风险尤为突出。本文采用数据包络分析(DEA)，构建地铁站风险控制有效性分析与评价的DEA模型，对地铁站拥挤踩踏风险进行定量分析。结合武汉地铁线上10个地铁车站的实际数据，从技术效率、规模效率和综合效率三个方面分析了拥挤踩踏风险控制效率；在此基础上，通过确定各决策单元松弛变量调整值，明确为达到风险控制的有效性应采取的改进策略，并利用松弛变量调整值与目标值间的差异辨识主要影响因素。采用DEA方法对地铁站拥挤踩踏事故风险分析结果与现状基本相符，可为判断地铁车站拥挤踩踏风险分析及制定改进策略提供决策依据。

数据包络分析(DEA)； 地铁站； 拥挤踩踏； 风险分析； 松弛变量

随着城市化建设，城市轨道交通作为一种运量大、方便快捷、舒适平稳的交通工具日益发展，增长的客流量使国内很多轨道交通超负荷运转，有限的地铁站空间导致车站拥挤成为轨道交通“特色”，地铁站人群拥挤踩踏事故风险也逐步增大。例如：2011年7月5日，北京地铁4号线动物园站A口上行扶梯发生设备故障，人群跌落导致踩踏事件，导致1人死亡28人受伤；2014年3月5日，广州地铁5号线一列车内，因两名少年恶作剧，引起乘客恐慌，逃跑过程中发生拥挤踩踏事件，导致13人受伤。据不完全统计，2008～2013年国内地铁共发生12起典型拥挤踩踏事故，导致98人伤亡[1]。因此，对地铁站拥挤踩踏事故风险进行分析有重要的实用价值。

目前，国内外对地铁工程安全管理主要集中在施工阶段的风险分析与评价。例如：国外对安全管理和危机管理的研究形成了英国伦敦地铁风险管理体系和美国地铁安全认证体系[2]等针对地铁施工的安全管理体系；我国学者也研究了地铁施工安全组织管理的影响因素[3]，确定了地铁工程施工安全风险识别规则[4]。随着地铁线路的建设与完善，大部分城市的地铁线路开始投入运营。由于运营时间短、客流量大、管理体系不健全等原因，实际地铁运营过程中存在诸多安全隐患，因拥挤造成踩踏事故的安全风险尤为突出。目前，史聪灵等[5]对地铁换乘站人群疏散进行了研究，宋维华等[6]对地铁运营安全风险管理进行了研究，但针对地铁站拥挤踩踏风险进行针对性的定量分析的文献较少。本文将针对上述背景，对定量评估地铁运营中拥挤踩踏的风险进行定量分析与评估研究。

目前常用的风险评价方法主要有事故树法、神经网络法及综合评价法等。这些研究方法大都需要明确具体的安全影响因素，并对各种因素赋权，容易受专家主观因素影响。但地铁站拥挤事故的发生受人、物、环境、管理四个方面的综合影响，各方面的影响因素都很多，且相互影响，因此采用这些方法定量研究地铁站拥挤踩踏事故风险需要建立庞大的研究体系。而数据包络分析(DEA，Date Envelopment Analysis )是通过定义输入变量和输出变量，并对变量值进行分析以评价系统的有效性，简化了复杂的影响因素确定过程，同时，DEA中模型的权重由数学规划根据数据产生，不需要事前设定投入与产出的权重，因此不受人为主观因素的影响。总之，数据包络分析是以变化权重评价决策单元的相对效率，显示相对有效性评价的一种重要方法。作为一种非参数的定量评价方法，DEA 方法能较好地排除诸多主观人为因素的影响，客观性和适用性强，在绩效评价、风险评估[7]、择优排序、预测组合有效性、决策单元等方面都有较好的应用。因此，本研究中，采用DEA法对地铁站踩踏事故风险进行定量分析，探讨地铁站拥挤踩踏事故的有效改进策略。

1 基于DEA的风险分析与优化

1.1 数据包络分析(DEA)

数据包络分析(DEA)由运筹学家Charnes A等于1978年率先提出，该方法主要用于评价多输入、多输出系统的相对有效性，对决策层安全风险的比较与评价提供技术支持[8]。由于DEA法具有不需要人为设定权重，且能从输入输出多角度对决策单元进行评价的优点，DEA方法多用于解决多输入、多输出的复杂系统问题。采用数据包络分析法进行有效性评价主要有以下优点：(1)能够分析多输入、多输出的决策问题；(2)不需要事先设定输入、输出指标的权重，而是根据数据规划原理产生，避免了主观因素的影响；(3)通过有效性分析，对于非DEA有效的决策单元能进一步确定指标的调整方向及调整值；(4)输入、输出指标间的关联关系不需要用关系式表示[9]。

为了适应DEA模型的发展，目前常用的适应不同规模收益的DEA模型有：测算生产是否为规模有效和技术有效的CCR模型，评价生产技术相对有效的BCC模型，满足规模收益非递增的FG模型和满足规模收益非递减的ST模型。这四种模型之间相互关联，研究中可根据约束条件、研究目的等的不同选择不同的模型。本文研究的地铁站拥挤踩踏风险用凸锥假设(即k倍的输入就能得到k倍的输出)描述缺乏准性，因此，本文采用BCC模型评价各单元的相对技术有效性。对地铁站踩踏风险的研究追求的是降低风险，因此本文以控制风险，即以产出为向导。

1.2 基于DEA的风险分析与优化

采用DEA方法评价决策单元有效性应按程序执行，其分析与优化过程如图1所示，具体包含以下7个步骤。

图1 DEA有效性分析流程

(1)确定评价目的：确定研究目的是用DEA方法解决问题的首要问题，一般是评价样本间的相对效率。

(2)确定评价单元：评价单元即研究对象，本研究选择地铁车站作为评价单元。

(3)选择输入/输出指标：输入输出指标是DEA评价的重要影响因素，指标选择的正确性会直接影响DEA的计算结果。

(4)建立评价模型：目前国内外已经建立了多种成熟的DEA模型，研究的目的、约束条件等不同时，DEA模型的选择也不同。

(5)输入/输出数据处理：根据选择的输入/输出指标，通过统计调查和资料查询等方式获得输入/输出指标的初始值。但实际调查中有些数据因不可得或不适用等原因，不能直接进行研究，需要结合数据间的关系进行相应转换和处理。使得能够以相同输入获得最大的输出，或通过最小的输入得到相同的输出，或综合调节输入、输出得到最小投入获得最大产出的效果。

(6)DEA有效性分析：根据DEA模型计算结果对应效益涵义的分析，确定各评价单元的相对有效性，确定各地铁站拥挤踩踏风险控制效率的相对有效性，并从技术效率和规模效率等方面对评价结果进行分析。

(7)基于非有效单元松弛变量调整改进策略：在DEA有效性分析的基础上，对于非DEA有效的决策单元，通过确定该决策单元指标松弛变量调整值确定为达到风险控制有效应采取的改进策略。并通过松弛变量调整值与目标值间的差异确定主要影响因素。其中松弛变量调整值为正表示应增加输入或减少输出，松弛变量为负表示应减少输入或增加输出。

2 地铁站拥挤踩踏事故机理模型构建

由于地铁拥挤踩踏安全管理是一个多输入多输出的复杂系统，采用DEA模型对地铁站拥挤踩踏风险进行分析时可以把各地铁站作为决策单元，通过各车站相对有效性评估确定拥挤踩踏风险水平。

2.1 输入输出指标确定

采用DEA方法对安全风险进行评价时，确定输入输出参数是影响模型有效性的关键。本研究综合考虑地铁站拥挤踩踏事故主要影响因素，并考虑到拥挤人群存在难以预测、局面难以控制及移动规律特殊等特点，将评估时段内客流量、站台面积、通道交叉次数、“瓶颈”点个数、出入口利用率标准差和疏导人员比例等6个指标作为输入参数，评估时段内滞留人数和疏散时间2个指标作为输出参数。实际上地铁站拥挤踩踏事故的发生还与楼梯、电梯、自动扶梯、各类通道以及出入口的通过能力有关，车站与地面间的位置关系如地面车站、高架车站和地下车站等也会影响乘客的安全疏散。但本文研究是以武汉市地铁车站为基础，考虑到武汉市地铁站通道设置通过能力足够，且绝大多数为地面车站，不考虑这些因素的影响。各输入输出参数量化处理过程如下。

2.1.1 输入因素

(1)客流量(x1)。人的因素往往是导致拥挤踩踏事故发生的关键，其他条件相同时，客流量增加会增加拥挤踩踏风险。为了统计方便，可以用指定时段内进出车站的人数作为客流量的表征值。

(2)站台面积(x2)。空间不足是拥挤最直观的感受。因此，充足的站台面积会直接避免拥挤，从而避免踩踏事故。站台面积值直接取站台长与宽的乘积。

(3)通道交叉次数(x3)。车站通道交叉口设计的合理程度及乘车点与出入口间通道交叉点的位置会直接影响客流速度，通道口处一般也更容易出现人群混乱，这些都是拥挤和踩踏的诱导因素。这里通道交叉次数取车站内通道交叉的次数之和。

(4)“瓶颈”点个数(x4)。人群滞留与混乱大多发生在通道变窄、门口、楼梯、台阶等通道突然变窄的“瓶颈”处，因此减少地铁站内“瓶颈”点的数量能直接降低地铁站拥挤踩踏风险。将站内所有通道突然变窄点总数作为各车站“瓶颈”点的个数。

(5)出入口利用率标准差(x5)。出入口设置的合理性直接影响车站人员分布，尤其当站内发生安全事故时，出入口成为影响客流密度的关键因素，各出入口客流量持平为最合理的状况。这里以各出入口利用率标准差表示平衡度，标准差越小表明利用越均衡，其值按公式(1)计算。

(1)

式中，α表示该车站的出入口利用率标准差；n表示车站出入口的总个数(个)；xi表示车站第i个出入口的客流量(人)；x表示车站n各出入口客流量的平均值(人)。

(6)疏导人员比例(x6)。出现拥堵时，疏导人员对控制拥堵事态至关重要。一般情况下疏导人员占总客流量的比例越大，越能有效指引乘客走向，减少乘客站内滞留时间，有效避免拥挤踩踏事件的发生。本研究疏导人员的比例取各地铁站疏导人员数量与评估时段内客流量的比值。疏导人员比例按公式(2)计算。

(2)

2.1.2 输出因素

(1)滞留人数(y1)。人群滞留是人群疏散过程最常见的人流形式，也是最容易发生拥挤踩踏的时段。人群滞留与人群移动速度间往往产生恶性循环，从而出现拥挤，导致踩踏事件发生。因此，将滞留人数作为决定拥挤踩踏风险的输出参数。在t时刻，特定区域的滞留人数NS用公式(3)表示，公式(4)、(5)是对公式(3)的说明。

(3)

(4)

(5)

式中，T为疏散总时间(s)；T0为开始发生人群滞留的时刻(s)；N1表示从疏散开始(t=0)到T时刻，n个分支入口汇集到出口的总人数(人)；N2为从疏散开始到T时刻出口疏散出的总人数(人)；fi(t)为通道第i个分支入口t时刻的人群流动系数(人/m·s)；f(t)为通道出口t时刻人群流动系数(人/m·s)；bi(t)为第i个分支入口t时刻人流宽度(m)；B(t)为通道出口t时刻人流宽度(m)，通常用出口宽度代替；n为分支入口数目(个)[10]。

(2)疏散时间(y2)。长时间处于紧张疏散状态会增加人群恐慌，人与人之间的不良影响也会成倍增加。有效缩短疏散时间是合理控制拥挤踩踏事故发生的最后环节，也是关键环节。因此，将此因素作为输出参数反应风险状况。疏散时间按公式(6)确定[11]。

(6)

(7)

(8)

式中， f为疏散点人群流动系数(人/m/s)，确定方法见式(7)；B为出口人流宽度，近似等于出口宽度(m)；Na为车站内需要疏散的总人数(人)；v为人群移动速度(m/s)，确定方法见式(8)；D为人群密度(人/m2)；其他符号同前。

2.2 地铁站拥挤踩踏风险评价DEA模型建立

根据前面的分析，地铁站拥挤踩踏风险分析采用基于产出的BCC评价模型。

式中，θ为相对效率；n为评价车站的个数；m为输入变量的个数；r为输出变量的个数；λj为各决策单元的系数；xj=[x1j,x2j,…,x6j]，x1j,x2j,…,x6j分别为第j个车站评估时段内的客流量、站台面积、通道交叉次数、“瓶颈”点个数、出入口利用率标准差和疏导人员比例；yj=[y1j,y2j]T，y1j,y2j分别为第j个车站评估时段内的滞留人数和疏散时间；ε为非阿基米德无穷小量，一般取10-6；s-和s+为松弛变量。

假设该模型的最优解为s*和θ*，则不同最优解组合对应的涵义如下：

(1)若θ*=1，且s*+=0，s*-=0，则决策单元满足DEA有效，即本系统中该决策单元在原始投入的基础上已实现最大产出。

(2)若θ*=1，但s*+和s*-中至少有一个不为0，则决策单元满足DEA弱有效，即该决策单元可以通过减少投入而保持产出不变，或保持投入不变而增加产出。

(3)若θ*<1。则决策单元为DEA无效，即该决策单元系统中，需要通过调整将客流量等输入参数降低为原来的θ倍而保持安全风险不变。

3 案例分析

本文以武汉地铁目前已运营的2号线与4号线中的街道口、江汉路、中南路、汉口火车站、武昌火车站、武汉火车站、洪山广场、光谷、循礼门、广埠屯共10个地铁车站(分别用A、B、C、D、E、F、G、H、I、J表示)为样本，进行实例分析。以2014年3月高峰时段地铁运营实况为研究对象，通过现场调查和相关方提供的参考资料为依据进行DEA有效性评价。

3.1 地铁站拥挤踩踏风险输入输出数据统计

根据建立的地铁站拥挤踩踏风险评价DEA模型及评价过程，通过搜集此10个车站的输入/输出原始数据，按照输入输出数据的要求，每个输入指标增加时，所有的输出数值都应相应增加。将本模型中输入参数站台面积和疏导人员比例进行同趋势化处理，这里采用同趋势化处理中常用的取倒数处理的方法进行转化[12,13]，并进行无量纲化处理，得到指标值如表1所示。

表1 车站高峰时刻输入、输出指标统计数据

3.2 拥挤踩踏风险控制效率分析

根据由统计数据得到的指标值，对这10个车站的输入、输出指标进行DEA分析，得到各地铁车站的拥挤踩踏风险控制效率如表2所示。

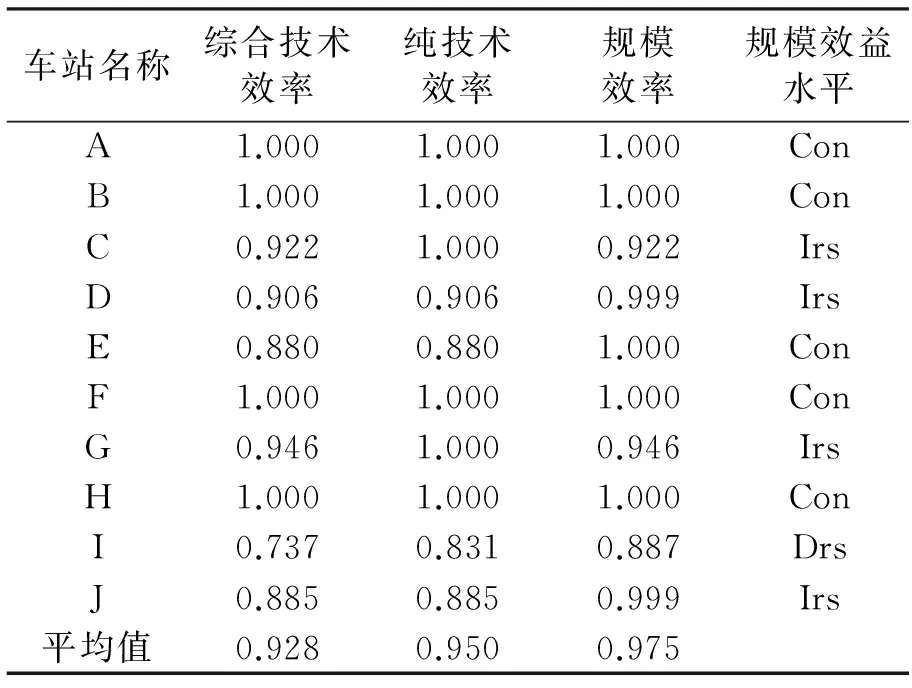
表2 各地铁车站拥挤踩踏风险综合效率值

注：综合技术效率=纯技术效率×规模效率，Con, Irs, Drs 分别表示地铁站处于安全风险管理水平规模效益不变、规模效益递增和规模效益递减区间。下同。

从表2中可以看出，只有A、B、F、H四个地铁站达到了风险控制相对有效水平，既达到技术有效又达到了规模有效。而其他七个车站拥挤踩踏事故风险控制工作离所能达到的标准还存在一定的差距，如I车站踩踏风险控制效率值为73.7%，说明该车站风险控制工作只达到了可实现水平的73.7%，还有26.3%的发展空间。10个车站的平均风险控制效率为92.8%，说明武汉市地铁站拥挤踩踏风险控制水平较高。

从纯技术效率的角度看，A、B、C、F、G、H六个车站拥挤风险控制均达到有效水平，与相对技术效率比较可以看出，虽然C车站和G车站没有完全达到相对有效，但技术上已达到标准要求，可从客流量等输入规模上考虑改进策略。10个车站平均技术效率值为95.0%，表明地铁站总体拥挤踩踏风险较低。从规模效率上也可以看出A、B、E、F、H 5个车站的规模满足要求，其他5个车站规模效率也较高。其中， C、D、G、J处于规模递增阶段，可增大车站规模，I车站处于规模递减阶段，可适当缩减规模以实现资源最优利用。在上面数值分析的基础上，为了进一步明确武汉市地铁站拥挤踩踏风险效率，以0.9的效率值作为临界点，从纯技术效率和规模效率两个方面将效率水平划分为四种类型。如图2所示。其中，第Ⅰ类为纯技术效率和规模效率均大于0.9的地铁站，这类车站拥挤踩踏风险控制较好。样本中A、B、C、D、F、H、G七个车站均为这类车站；第Ⅱ类为纯技术效率在0.9以上，但规模效率小于0.9，这类车站应注意改进车站输入指标规模。样本中E、J属于这类车站；第Ⅲ类和第Ⅱ类恰好相反，应注重客流量管理等风险控制技术的改善。样本中I车站属于这类车站；第Ⅳ类为在规模和技术上都应严加管理的车站，本文样本中不存在这样的车站。

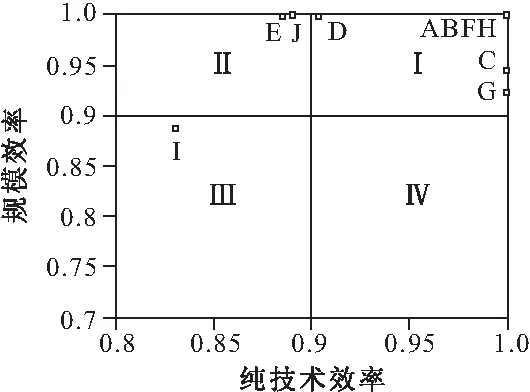
图2 地铁站纯技术效率及规模效率分布

3.3 各地铁站风险控制指标松弛变量分析

为了对各非DEA有效的地铁站提供改进建议，采用DEA分析软件对10个地铁车站进行松弛变量调整，得到10个车站的输入输出变量调整值如表3所示。通过分析各输入输出指标的松弛变量，确定各方面风险控制的合理性，并给出调整建议。

表3 各地铁站输入、输出变量调整值

注：S为松弛变量调整值；P为目标值。如：Sx1表示客流量的松弛变量调整值；Px1表示客流量的改进目标值。

从表3中可以看出各输入输出变量松弛变量调整值和目标值之间的关系。通过确定调整值与目标值之间的比例就能得出影响风险控制效率的关键因素，比例越大说明对有效性的影响越大。整体上看，A、B、C、F、G、H地铁站的各指标不用调整，需要调整的车站指标之间的调整比例也有差异。以D地铁站为例，输入指标方面，客流量、站台面积、 “瓶颈”点个数、出入口利用率标准差、疏导人员比例五项输入指标均需要调整，客流量指标调整量为减少3.46，和目标值6.79的比值为0.51，其余指标用类似方法计算得到调整量与目标值的比值分别为：0.29、0.17、0.49、8.14。分析数据可以看出，疏导人员比例调整值与目标值比例为8.14，调整比例最大，因此，D车站效率值不达标的主要影响因素为疏导人员比例，实际运营中增加疏导人员比例，以实现安全疏散。根据松弛变量调整值正负的含义以及指标值与实际值之间的关系，还能判断各地铁站各项指标的实际调整建议。以E车站为例，输入指标x1～x6的松弛变量调整值分别为：-1.68、-0.33、0、-0.67、-0.98、-7.00，说明为了实现拥挤踩踏风险控制最优效率，该车站应减少客流量、适当增加站台面积、维持交叉点数目、“瓶颈”点处应进行处理保证乘客流通、出口的设置不够合理、疏导人员比例应适当提高。从十个车站整体输出指标方面考虑，需要控制的是疏散时间，因此车站管理中应加强疏散管理意识，配置更有效的疏散设备，提出更合理的疏散方法以缩短疏散时间。

3.4 指标调整后安全风险分析

为了研究DEA松弛变量调整对地铁站拥挤踩踏风险控制效率的意义，将各指标基于松弛变量调整分析得到的目标值作为新数据输入，分析各地铁站调整后的风险控制效率，如表4所示。从表4中可以看出，除C和G地铁站外，各地铁站均同时达到了技术有效和规模有效，这两个车站的纯技术效率也达到有效水平，需要进一步对整体规模进行调整。同时，从分析结果可以看出，基于松弛变量调整对地铁站各项输入输出指标进行调整分析，并按照建议调整各指标值，能显著提高风险控制水平，松弛变量值分析对改进车站管理水平具有指导性的意义。

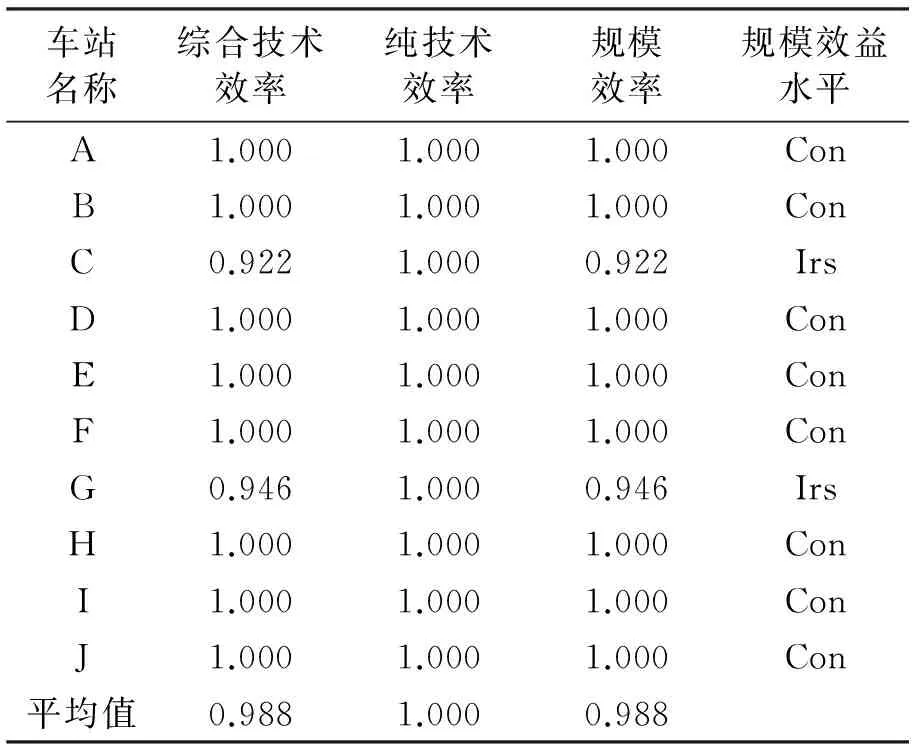
表4 基于松弛变量分析调整后各地铁站 拥挤踩踏风险效率分析

3.5 地铁站拥挤踩踏风险控制建议

本文案例研究采用的10个地铁站是目前武汉市地铁站中拥挤踩踏风险较大的车站，通过对这些地铁站进行分析，针对武汉市大中型地铁车站拥挤踩踏风险控制有以下三点建议：

(1)从拥挤踩踏风险控制效率来看，A、B、F、H四个车站的效率水平已达到最优，从纯技术效率上看C、G车站的效率也达到最佳。加强武汉市地铁站拥挤踩踏风险管理应注重学习这些车站的建设布局及疏散管理。相对而言，I车站的效率值较低，应加大改善力度。

(2)从非有效车站的松弛变量调整值中可以看出，出口利用率和疏导人员比例存在的问题相对较大，可以采用在人流量大的出口增设出站口和增加疏导人员比例来实现。这两方面的改善成为非有效车站改善重点。同时可以看出，在规模可变的BBC评价模型下，松弛变量调整的对象为技术效率不达标的决策单元。

(3)从综合效率、纯技术效率和规模效率的值可以看出，C和G地铁站虽然达到了技术有效，但规模设置不合理，可以适当减小规模实现资源优化配置。已建成的车站缩减规模不太符合实际，但可以在后续地铁建设中加强规模考虑。而D、E、J车站的非有效性主要体现在技术效率不达标，应注重安全管理。I车站综合效率不达标受纯技术效率和规模效率影响均较大。

4 结 语

DEA数据包络分析法适用于处理“多方案选择—多影响因素”等研究和解决方案有效性的问题，能较好地排除诸多主观因素的影响，客观性和适用性强，具有简便快捷等优势，结合工程实例表明可将其用于地铁车站踩踏风险分析与评价，并为制定疏散控制改进策略提供决策依据。

(1)本文提出了DEA风险分析与优化方法，结合本文分析的实际内容选择了基于产出的BCC评价模型。根据地铁站拥挤踩踏事故的影响因素分析，选取客流量、站台面积、通道交叉次数、“瓶颈”点个数、出入口利用率标准差和疏导人员比例等6个可量化指标作为输入参数，以滞留人数和疏散时间为输出参数，构建地铁站风险控制有效性分析与评价的DEA模型。

(2)从技术效率、规模效率和综合效率三个方面分析地铁站拥挤踩踏风险控制效率，可看出武汉地铁站风险控制整体水平较高。A、B、F、H四个地铁站风险控制达到相对有效水平，其他车站风险问题主要存在于运营规模。采用纯技术效率和规模效率分布图可直观看出各地铁站风险控制水平。

(3)通过分析各地铁站各项指标的松弛变量调整值，明确为达到风险控制有效性应采取的改进策略。结果表明6个车站的指标不用调整，需要调整的指标的调整比例也存在较大差异。并通过分析调整值与目标值之间的比例，确定影响各非有效车站有效性的关键因素。

[1] 李为为，唐祯敏. 地铁运营事故分析及其对策研究[J]. 中国安全科学学报，2004，14(6)：108-111.

[2] 王起全. 基于赋权关联度算法的地铁拥挤踩踏事故风险研究[J]. 中国安全科学学报，2013，23(5)：94-100.

[3] 吴贤国，刘惠涛，张立茂，等. 地铁施工安全组织管理影响因素分析[J]. 土木工程与管理学报，2012，29(4)： 79-83.

[4] 余宏亮，丁烈云，余明晖. 地铁工程施工安全风险识别规则[J]. 土木工程与管理学报，2011，28(2)：77-81.

[5] 史聪灵，钟茂华，张 岚，等. 地铁换乘车站客流疏运模拟及风险分析(2)——单通道换乘车站[J]. 中国安全生产科学技术，2011，7(8)：21-28.

[6] 宋维华，殷位洋. 地铁运营安全的风险管理[J]. 城市轨道交通研究，2009，(2)：59-61.

[7] 王凤山，吴华杰，卢厚清，等. 基于DEA的地震作用下岩石边坡工程整体安全风险分析[J]. 地下空间与工程学报， 2011，7(4)：789-794.

[8] 魏权龄. 数据包络分析(DEA)[J]. 科学通报，2000， 45(17)：1793-1808.

[9] 杜 栋，庞庆华. 现代综合评价方法与案例精选[M]. 北京： 清华大学出版社，2008.

[10]张青松，刘金兰，赵国敏. 大型公共场所人群拥挤踩踏事故机理初探[J]. 自然灾害学报，2009，18(6)： 81-86.

[11]赵国敏，倪照鹏，张青松. 地铁车站人员疏散离散时间模型研究[J]. 防灾减灾工程学报，2010，30(2)：152-157.

[12]徐勋建，陈泽西. 基于TOTPIS的电网融冰决策技术IDSS研究[J]. 湖南大学学报(自然科学版)，2012，39(12)：62-67.

[13]李 亮，崔晋川. DEA方法中输入输出项目的选择和数据处理[J]. 系统工程学报， 2003，18(6)：487-490.

Risk Analysis of Crowded Stampede Accident in Subway Stations Based on DEA Method

ZHANGLi-mao,LIUMeng-jie,WUXian-guo,ZHONGJing-bing

(School of Civil Engineering and Mechanics, Huazhong University of Science and Technology,Wuhan 430074, China)

Many potential safety hazards exist in metro operation due to short operating time, big traffic, and incomplete management system and so on. The security risks caused by the crowded stampede accident are particularly acute. The data envelopment analysis (DEA) is used to quantitatively analysis the crowded stampede risk. According to the data of ten subway stations in Wuhan metro system, efficiency analysis in terms of technical efficiency, scale reward and comprehensive efficiency is concluded. Based on this, by determining each decision-making unit’s slack variable modifier, the improvement strategies are subsequently made, and the main factors are identified. Results indicate that the crowded stampede accident risk assessment is consistent with actual situation. Thus, DEA method can be used in determining the crowded stampede risk status in the station, as well as making improvement strategies.

data envelopment analysis (DEA); subway station; crowded stampede; risk analysis; slack variable

2014-06-20

2014-09-02

张立茂(1987-)，男，湖北荆州人，博士，研究方向为工程安全管理(Email:limao_zhang@hotmail.com)

刘梦洁(1992-)，女，湖北钟祥人，硕士，研究方向为地铁运营管理(Email:lmj0314@163.com)

国家自然科学基金(51378235)；武汉市建委科技项目(201208； 201334)

U291.69

A

2095-0985(2014)04-0076-07