交变载荷作用下埋地天然气管道受力特性

同济大学 刘东京 周伟国 滕卯寅 潘新新

关于管道受力分析，国内外主要研究在特殊工况下的管道受力特性，如地层塌陷、地基沉降、冲蚀破坏等条件下的管道受力分析。天然气管道通常埋设在路面以下，直接或间接作用在埋地管道上的载荷主要有管道结构自重、填土压力等恒载，以及交通载荷、地面堆载、管道内压等载荷。其中，内压、土载、外载是埋地管道最主要和作用最频繁的载荷。土载在有限元分析中一般作为静载考虑，载荷计算依据各层土的性质。内压波动和外载(或交通载荷)即为交变载荷。交通载荷按照随时间是否变化，可分为静载荷和动载荷两大类，本文主要对管道的动载荷模型进行研究。

对于深埋天然气管道，可将车辆轮胎载荷近似地简化为路面集中点载荷；线载荷也是对真实轮胎载荷的近似，可用于平面分析模型中；面载荷最接近于轮胎的实际接地轨迹，一般用于三维浅埋的埋地管道分析模型。由于城市燃气埋地管道埋设深度不会很深，为了满足某些特定环境下管道的铺设，还要在强度要求下尽量浅埋，因此三维模型采用矩形面源载荷进行处理。

1 有限元模型

1.1 建模方法

(1)几何模型。管道采用各向同性的线弹性体模型；回填土部分采用弹塑性体模型；地基若是条件好的硬基，则采用线弹性体模型，若是土性差的基础，则采用弹塑性体模型。

(2)土体模型。管土相互作用的回填土模型，根据实际填土情况简化为三层，由上至下依次为面层、基层以及地基层。地基层的土壤性质由现场环境决定，基层为埋管周围回填土，多采用砂土或者原状土，面层为原状土或者路面混凝土。

(3)单元模型。采用空间8节点协调单元，管道和土体均采用固体单元。

(4)约束模型。模型底面采用链杆支座，不允许有垂直方向的位移；模型各侧面对法线方向进行约束，填土表面属于自由边界。

(5)接触模型。管土接触采用有限元摩擦接触模型。分析土体与埋地管道结构相互作用时，认为管土接触面为非完全接触，径向位移相等，环向发生滑移。回填土与地基接触面认为是完全接触。

1.2 算例模型

(1)管道参数。假设管道计算管长与管沟长度均为6 m，管径325 mm，壁厚8 mm；钢管的材质Q235钢，弹性模量2.1×1011Pa，密度7 800 kg/m3，泊松比0.3。

(2)回填土参数。在计算模型中，回填土为亚粘土，其弹性模量为3 450 kPa，密度1 900 kg/m3，粘聚力为32.0 kPa，摩擦角为18.3。地基土呈自然平衡状态，容重等于0。

(3)载荷参数。钢管最大内压为2 MPa，交通载荷外载以动载形式作用于管道上方，载荷作用区间简化为0.4×1.2 m的矩形，外载最大为0.5 MPa。土载在有限元分析中作为静载考虑，载荷计算依据各层土的性质。

2 结果与讨论

2.1 移动载荷

假设移动载荷为恒幅载荷0.3 MPa，管道埋深0.8 m。移动载荷从管道一侧开始施加，随着时间的增加，外载作用位置向管道另一侧转移，当到达另一侧时，载荷沿着原作用位置逆序返回，记为一个周期。由图1和图2可知，当载荷初次通过管顶时，管道各点竖向位移振荡减小，稳定后再次返回原作用点时，管顶位移由于产生土体的缓冲作用，竖向位移较载荷初次作用时有一定程度的减小。在管道两端处，管侧应变值最大，管顶和管底应变值相对较小；当移动载荷作用在管道上方时，对管顶和管底应变的影响不是很大，主要受力影响发生在管侧位置。

图1 移动载荷对管道两端各点竖向位移的影响

图2 移动载荷对管道两端各点应变的影响

2.2 内压变化

内压波动采用三角波进行模拟，在一个周期内，内压从初始最小值0 MPa上升到最大值，然后又线性变化回初始值，管道埋深均为0.8 m。分别考虑在不同外载作用下，内压变化对埋地天然气管道受力特性的影响。

2.2.1 外载0 MPa，内压最大0.4 MPa

由图3和图4可知，随着管道内压的波动，管道两端各点应变值也相应变化。在内压最大时，管道各点应变达到最大值，管底竖向位移同样最大，管顶和管侧竖向位移最小，且管侧竖向位移变化幅度明显小于管顶；在内压降到0 MPa时，管顶竖向位移大于管侧和管底竖向位移，且管底竖向位移最小；在内压达到0.4 MPa时，管道两端各点竖向位移呈相反变化。

图3 外载0 MPa内压0.4 MPa对管道两端竖向位移的影响

图4 外载0 MPa内压0.4 MPa对管道两端应变的影响

2.2.2 外载0.3 MPa, 内压最大0.8 MPa

由图5和图6可知，在管道中心位置处，管顶和管底应变变化趋势基本相同，在内压最大时出现波谷，且均随着内压的增大而减小；管侧应变相对较大，且在内压最大时达到最大值，应变随内压的增大而增大。管顶、管侧、管底处竖向位移变化规律基本相同，呈波浪式起伏变化，且变化范围随内压增加逐渐减小。

图5 外载0.3 MPa内压0.8 MPa对管道中心位置竖向位移的影响

图6 外载0.3MPa内压0.8MPa对管道中心位置应变的影响

2.2.3 外载0.1 MPa，内压最大2 MPa

由图7和图8可知，管道受内压作用，竖向位移变化规律与内压最大值为0.4 MPa、0.8 MPa时基本相同，但竖向位移相对较小；载荷作用时间越长，竖向位移变化趋势越稳定，最后趋于平缓。管道各点应变为周期性变化，管顶和管底应变变化趋势基本相同，随内压增加，先小幅降低，然后逐渐增加，在内压最大时达到最大值，之后又逐渐降低，在与初始拐点对称位置出现曲线的第三个拐点，此后应变逐渐增加。管道中心处管侧应变高于管顶和管底的应变，且随内压的增加，应变逐渐增大，在内压最大时达到最大值，之后逐渐减小。

图7 外载0.1 MPa内压2 MPa对管道中心位置竖向位移的影响

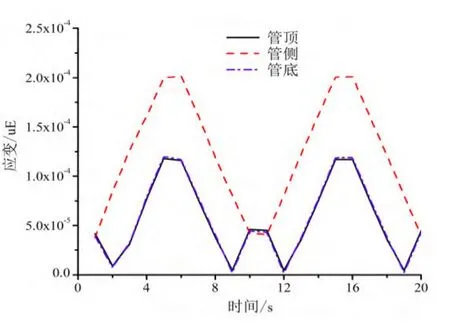
图8 外载0.1 MPa内压2 MPa对管道中心位置应变的影响

3 结语

当移动载荷作用在管顶上方时，对管顶和管底的应变影响不是很大，主要作用产生在管侧位置。管顶竖向位移变化较为显著，当载荷初次通过管顶时，管道各点竖向位移先振荡减小，稳定后再次返回原作用点时，管顶位移由于产生土壤的缓冲作用，竖向位移较初次作用时有一定程度的减小。随着管道内压的波动，管道各点应变也相应变化，在内压最大时管道应变达到最大值，管顶和管侧竖向位移则最小，管侧竖向位移变化幅度明显小于管顶。