用于高精度实时动态定位的整周模糊度解算

来毅，王党卫，翟建勇，袁润平

(中国电子科技集团公司第二十研究所，西安 710068)

0 引言

实时动态（Real Time Kinematic, RTK）定位是一种为动态用户实时地提供高精度定位的技术，具有定位精度高、实时性好和算法鲁棒性强等优点，因而受到了工业界和学术界越来越广泛的关注。RTK定位技术在军事、农业、建筑和工程测绘等重要领域有着非常广阔的应用前景。比如，在房地产测量中，应用 RTK技术来实时测定每一宗土地的有关权属界址点及相关地物点的位置，可达到厘米级的测量精度。RTK定位技术的基本思想[1,2]是：基准站接收机和移动站接收机同步观测共视卫星，采用模糊度快速解算技术，对卫星载波信号进行平差处理，以获得整周模糊度初始值。移动站在此初始化的过程中因保持运动而产生的位移和瞬时位置，可由随后确定的整周模糊度根据所谓逆向求解技术来确定。

RTK定位技术最核心的问题就是快速获得正确的载波相位整周模糊度。一旦模糊度固定，载波相位测量就相当于高精度伪距测量[3]。一般情况下，采用经典的最小二乘方法可以获得一个整周模糊度解，但此模糊度解通常不是整数值，称之为浮点解或实数解。事实上，模糊度解的真值应该是整数值，因此，必须对浮点解作进一步处理。在 RTK高精度测量时，根据模糊度的浮点解求得其整数解的过程叫做整周模糊度的固定。只有正确的固定了整周模糊度，才能获得较高的测量精度。

为了使移动站接收机在运动过程中快速获取整周模糊度，国内外很多学者对此进行了深入的研究，提出了一系列的算法。FARA（Fast Ambiguity Resolution Approach）搜索法[4]根据实数解的方差来确定整数值的搜索范围。模糊度函数法[5]通过构建一个包括模糊度向量和位置参数向量的函数并使该函数值达到最大，从而得到位置参数和模糊度的最佳估值，该方法使得在实时的情况下，依然能够求解出位置参数。然而，FARA搜索法和模糊度函数法求解模糊度的搜索时间过长，而且对解的统计性进行研究也不是很方便，因此，很难称得上是一种严密的方法，更不可能形成一个严密而又完整的理论体系。整数最小二乘方法应用整数最小二乘原理对模糊度进行整数估值，其中，LAMBDA（Least-Squares Ambiguity Decorrelation Adjustment）算法因较好的搜索性能和完善的理论体系而被广为接受[1,2,4]。它既可应用于静态定位系统，又可应用于实时动态系统，因而具有很大的实际应用价值。

本文针对整周模糊度解算问题过程中的搜索空间的建立、搜索空间的大小和形状、搜索效率、搜索过程和模糊度的判定准则进行了深入分析和系统研究，实现了一种具有较强实用性的高精度实时动态定位算法。实验结果表明，本文算法可减少整周模糊度的收敛时间，提高整周模糊度的实时性。该算法对GPS和GLONASS数据均可实现毫米级的精确定位，可为我国自主研发高精度实时动态定位技术提供技术参考。

1 整周模糊度解算

高精度实时动态相对定位的关键就是载波相位整周模糊度的动态确定。当接收机锁定卫星信号之后，载波相位变化的整周部分便被自动计数，不足一周的小数部分可以通过接收的卫星信号相位和接收机的本地载波相位得到。本节以整周模糊度解算的基本原理为基础，以整周模糊度解算的流程为线索，将对其进行深入分析和详细讨论。

在根据经典最小二乘求得模糊度和坐标向量的浮点解， 和相应的协方差阵后，以整数向量a与浮点解之间的距离平方为目标函数，搜索整周模糊度a，使得这一目标函数达到最小值，即

满足式（1）的整数解记为最优解。具体来讲就是首先求出序贯条件最小二乘模糊度，再通过序贯条件最小二乘模糊度来构建目标函数，以使其值达到最小从而求得模糊度的整数估计值。其中第二步为求解模糊度的核心，它包括了模糊度空间的构造、模糊度搜索、模糊度空间尺寸确定、模糊度检验和逆变换等关键问题。

1.1 模糊度的整数变换

为了更好更快地求解双差模式下的整周模糊度，使得搜索空间的形状变得更为有利于快速搜索到最优解，则事先必须对其进行整数变换，以便降低在整周模糊度的相关性。简单的来说，整数变换的目的就是为了降低双差模糊度的相关性。若a为原始模糊度，通过变化而得到的新模糊度为z，则其整数变换可表示如式（2）所示。

其中，Z为模糊度的整数变换矩阵。Z变换必须保证变换后的模糊度仍然是整数，且变换过程应是可逆的。变换矩阵Z的构造步骤如下：

（1）对正定的方差阵 Da进行LD分解，得到下三角矩阵 L1和对角阵；

（3）对Da计算变换后的协方差阵：

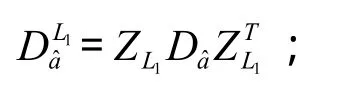
（5）对U1取整，即表示对U1取整；

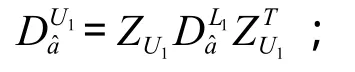
（8）最终的整数变换矩阵为：

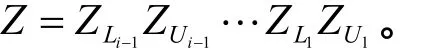
1.2 模糊度搜索

序贯条件最小二乘模糊度是用模糊度的浮点解通过式（3）来计算的：

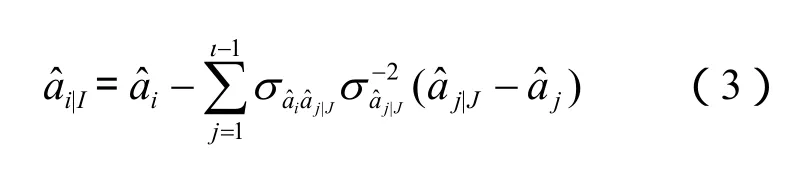
其中，是的简写，表示第i个模糊度是以前面i- 1个模糊度固定到整数值为条件的最小二乘整数估计，σij|J表示与之间的协方差。一个重要的性质是，所有序贯条件最小二乘模糊度之间都是不相关的，即的方差阵是一个对角阵，在式（3）的两边都减去第i个模糊度的真值，可得：

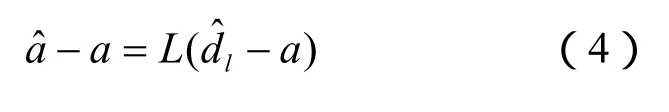
对式（4）进行搜索，建立如下的目标函数：

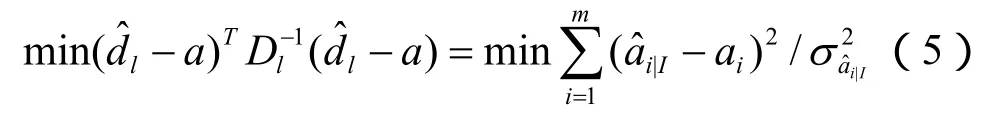
通过使目标函数式（5）达到最小值来求得模糊度向量的固定解（整数解），这就是整周模糊度求解方法的基本原理。可见，所求得的模糊度固定解与用整数最小二乘法得到的完全相同，但比整数最小二乘法求解速度更快。因此，该整周模糊度解算方法是整数最小二乘方法的发展，从某种意义上讲，是一种更好的整数最小二乘方法。

1.3 确定搜索空间

实际计算时，基于目标函数式（5）的极值问题就是通过不断的搜索来实现的。需要选取一个适当的2χ值，则此时的模糊度搜索空间可表示为：

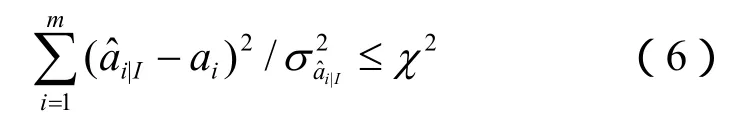
显然，这样的搜索空间是一个m维的超椭球。

为了得到合理的2χ值，采用如下处理方法：首先对全部取整，将获得最接近它的整数矢量，这是就得到了一个整数矢量1a，然后将1a中的一个元素保持原值，其他元素取次接近的整数，对于m维整数矢量1a而言，可以构造出m个这样的整数矢量，这样总共可以得到 1+m个整数矢量，利用所得到的整数矢量集，分别替代式（6）中的a，取等式成立计算出相应值，这时可以得到 1+m个不同的数值，取其中次最小的2χ值，构造模糊度搜索空间，这样可以保证搜索空间中至少包含两个整数矢量。实际上采用这种方法构造的搜索空间，所包含的整数矢量个数不会太多，因此有利于快速搜索。

1.4 模糊度检验

模糊度检验是指对搜索空间中所有可能的模糊度组合进行检验，选出正确概率最大的组合作为整周模糊度的最终解。目前，最常用的一种比值检验方法是比较次最小残差平方和与最小残差平方和的模糊度组合比值，建立相应的目标函数为：

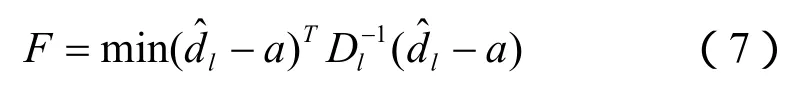
对搜索空间中每对可能出现的模糊度组合，利用式（7）求出其相应的F值。在此过程中将F值为最小和次小的组合保留，相应的F值记为F1和F2。当搜索结束后，用F1和F2的值进行ratio检验。

为了确保所得整周模糊度的正确性，若在一段时间内同一组模糊度满足上述关系方程，则认为该组模糊度为正确的模糊度。若不存在比值比ratio值大的模糊度组合，则认为求解失败。

1.5 逆变换

通过搜索求得变换后得到的整周模糊度向量的固定解˘。对按式（9）进行逆变换求得模糊度的固定解：

至此，模糊度的解算与固定完成。

2 高精度实时动态定位系统

本文以如前所述的整周模糊度解算方法为基础，实现了一种高精度实时动态定位系统。该系统主要包括以下六个模块：

（1）数据接口模块，可实现不同格式文件的读取；

（2）卫星位置计算模块：利用广播星历或者精密星历计算卫星位置；

（3）单点定位模块：利用单历元数据计算接收机的概略位置；

（4）模糊度解算模块：以浮点解为基础，根据第二节所述算法解算得到模糊度固定解；

（5）周跳检测与修复模块：利用TurboEdit方法实现了周跳检测与修复；

（6）基线向量求解模块：利用固定的整周模糊度求解出移动站和基准站之间的基线向量，即

3 实验结果与分析

为了验证本文所给出的高精度实时动态定位算法的有效性和可靠性，分别针对采集到的GPS和GLONASS两类具有不同特性的数据进行了测试，并将得到的结果与真实值进行比较。其中，历元时间间隔均为1s，ratio值门限设为3。

采集GPS数据时，利用两个NovAtel双频接收机板卡，基准站型号为FLEXPAK-OEMV-6接收机，移动站型号为 OEMV-IDF-RT6，均用型号为GPS-702-GG的双频天线，两天线固定在基线长度为14.575m的两端A、B。采集GLONASS数据时，利用 GLONASS接收机进行采集，基线长度为5.450m。

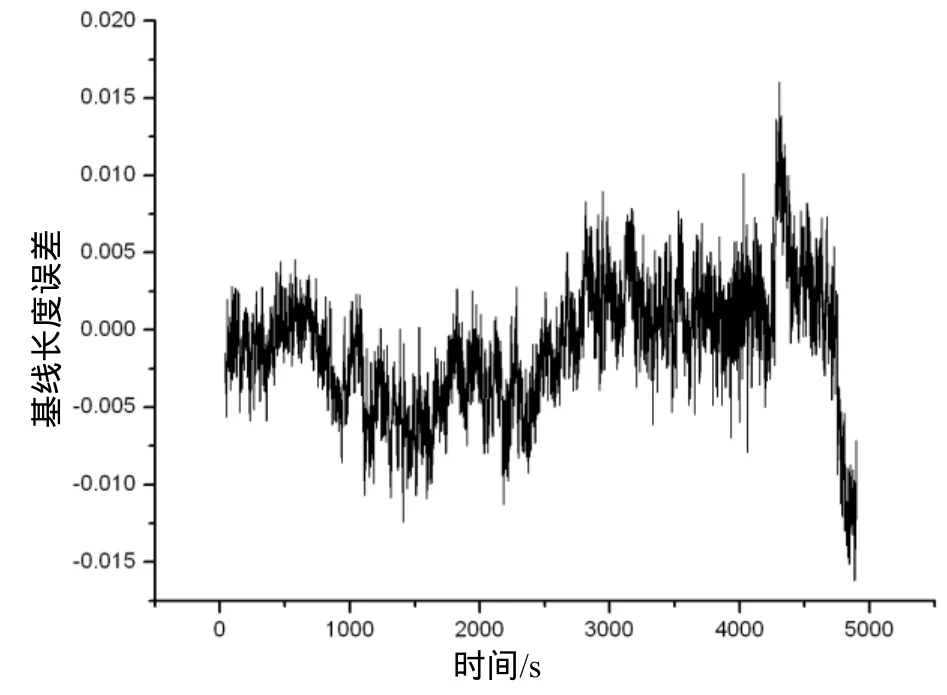
图1 GPS数据测试基线误差

由图1和图2所示结果可以看出，基线长度的稳定性是比较好的，其误差在 5mm内，基本上能满足测量的要求。理论上，载波相位定位可以达到更高的精度，但由于测量的原因及多路径效应的影响，使载波相位的观测值会有一定的抖动造成了定位误差的加大。

图1和图2分别是针对GPS和GLONASS数据的测试结果，其中横坐标表示解算该基线作用的历元数， 纵坐标是解算的基线长度与真实基线长度的误差。从图1中可知，对于GPS测试数据，所解得的基线平均长度为14.5740m，方差为0.0048。从图2中可知，对于GLONASS测试数据，所解得的基线平均长度为5.4521m，方差为0.0027。

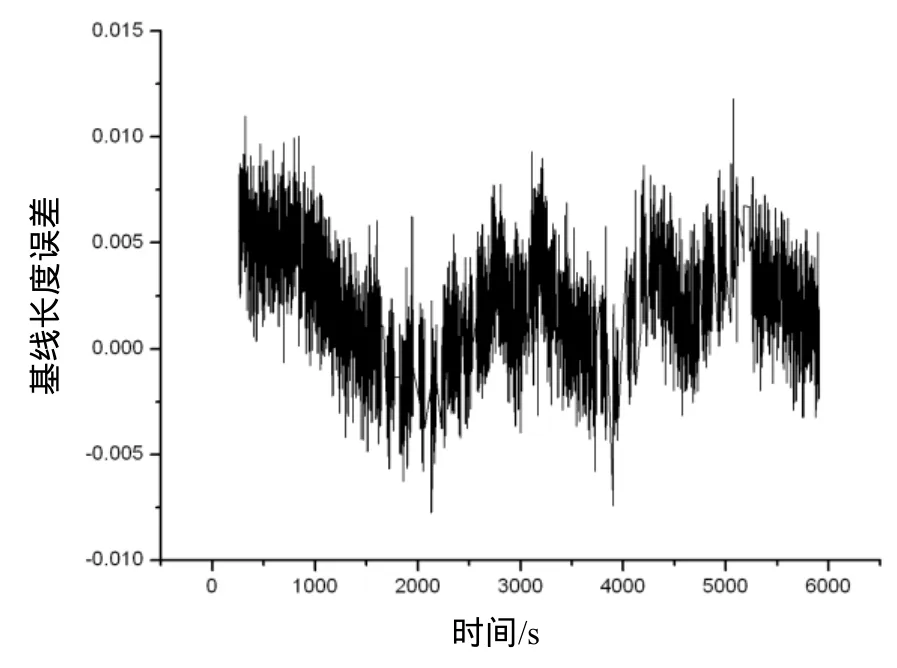
图2 GLONASS数据测试基线误差

4 结论

本文主要针对 RTK中最关键的技术――整周模糊度解算进行了深入分析和详细讨论，并以此为基础，给出了一种 RTK算法实现流程，实现了一种高精度实时动态定位算法。利用所实现的 RTK系统，对GPS和GLONASS数据进行处理，实验结果表明，该算法对GPS和GLONASS数据均可实现毫米级的精确定位。在后续研究中，期望能将该处理流程更加完善，以增强其可靠性。

[1] Teunissen PJG. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation [J]. Journal of geodesy, 1995(70): 65-82.

[2] P.J.G. Teunissen, P.J. de Jonge, .C.J.M.iberius. On the spectrum of the GPS DD-ambiguities. Proceedings of ION GPS-94, 7th International Technical Meeting of the Satellite, Division of the Institute of Navigation[C]. Salt Lake City, UT, 1994, 115-124.

[3] 徐绍铨等. GPS全球定位系统及其应用[M]. 武汉: 武汉测绘科技大学出版社，2001.

[4] 谢钢. GPS原理与接收机设计[M]. 北京：电子工业出版社. 2009.

[5] Frei.E and Beutler.G. Rapid static positioning based on the fast ambiguity resolution approach (FARA) [J]. theory and first results, Manuscripta Geodaetica,1990,1059-106.