可倾瓦气体轴承气膜厚度的计算和分析

程进杰，孙郁，孙立佳，季伟，张武,2

(1.中国科学院 理化技术研究所，北京 100190，2.航天低温推进剂技术国家重点实验室，北京 100028)

符号说明

b——轴承宽度，m

B——轴瓦厚度，m

Cb——半径间隙，m

Cp——名义半径间隙，m

d——转子内径，m

ex——轴心在x坐标上的值，m

ey——轴心在y坐标上的值，m

E——转子的弹性模量，GPa

f——密度分布概率

F——动压气膜力作用在轴瓦上力的矢量

h——气膜厚度，m

hm——平均气膜厚度，m

h(θ)——θ方向上的气膜厚度，m

I——截面惯性矩，m4

K——刚度矩阵

M——弯矩，N·m

Oj——轴心位置

Opad——轴瓦中心位置

P——气膜压力，Pa

rg——离心力引起的轴的变形量，m

R——轴半径，m

R0——初始状态下的轴半径，m

Rb0——初始状态下的支点圆半径，m

Rbearing——支点圆半径，m

Rp0——初始状态下的瓦半径，m

Rpad——轴瓦半径，m

S——轴瓦弧长，m

t——时间，s

v——轴颈表面的周向运动速度，m/s

αp——线胀系数，℃-1

β——轴承偏斜角度，rad

βi——第i轴瓦的支点位置角，rad

ΔTp,ΔTs——轴瓦和轴的温差，℃

λ——轴承的偏斜程度

δ1——轴瓦半径的膨胀变形，m

δ2——轴瓦厚度的变化量，m

δ3——轴的热变形量，m

δ4——轴瓦的弹性变形量，m

δi——轴瓦的摆角，rad

δtotal(θ)——在考虑轴瓦和轴的热力变形时，θ方向上气膜厚度的变化量，m

ε0——转子在中心平面的偏心率

θ——沿轴承轴向的角坐标，rad

λe——轴承的偏斜率

λm——轴承的最大偏斜率

μ——气体的动力黏度，Pa·s

ν——泊松比

ρ——轴密度，kg/m3

σ——表面粗糙度的标准差

φ——轴承轴向上轴的偏心角，(°)

φ0——偏斜条件下的姿态角，(°)

ψ——承载方向的偏斜平面和轴向平面的夹角，(°)

ω——轴的转速，r/min

1 概述

相对于传统的滚动轴承和滑动轴承，气体轴承具有转速高、摩擦损失小、寿命长、噪声低、无污染和工作温度范围广等优点，在很多领域得到了广泛应用，如透平膨胀机、高速牙钻、高速主轴、惯性陀螺仪等。

根据气膜压力产生的原理,气体轴承大致分为挤压膜气体轴承、静压气体轴承和动压气体轴承3种。动压气体轴承由于不需要供气系统，降低了装置的复杂性，另外，由于不需要耗费高压气体，提高了运行的经济性，且动压效果随表面相对运动速度的增加而愈加明显[1]。

目前，较为常见的几种动压气体轴承结构形式有可倾瓦型、螺旋槽型、人字槽型、阶梯型和箔片型等。可倾瓦轴承由于轴瓦可以绕枢轴摆动，各轴瓦均能自由倾斜，具有良好的稳定性和自对中能力，在旋转机械中得到了广泛应用，特别是在高速透平机械中日益受到青睐。

可倾瓦气体轴承一般由多片可绕其枢轴自由旋转的轴瓦构成，结构如图1所示，为了便于显示，放大了轴和轴瓦的间隙。当系统承受载荷时，每片轴瓦都会根据载荷补偿气膜厚度的改变，并产生相应的气膜压力保持平衡，以达到稳定状态。

图1 可倾瓦动压气体轴承结构简图

目前主要研究的是可倾瓦油润滑轴承，对可倾瓦气体轴承的研究相对较少。而且研究的方向主要侧重于轴承的稳定性、刚度、阻尼系数、承载力、偏斜比和偏心比等方面，很少涉及到热力变形、轴线偏斜、离心变形和表面粗糙度等结构参数。由于气体轴承的半径间隙很小(0.02 mm左右)，高转速下这些影响因素不可忽略[2]。

2 基础理论

气体润滑轴承的动静性能计算均会涉及到Reynolds方程的求解，求解该方程首先需要求解气膜厚度，忽略气体动力黏度随温度的变化，等温条件下的气体润滑Reynolds方程为

(1)

气膜厚度的计算公式为[2]

h=Cp-(Cp-Cb)cos(θ-βi)-(R+

B)δisin(θ-βi)+excosθ+eysinθ。

(2)

然而可倾瓦气体轴承很少能够在理想状态下运行，实际运行中的离心力变形、轴瓦和轴的热力变形、制造和安装误差等，都会影响轴承的气膜厚度。

3 气膜厚度的影响因素

研究的可倾瓦气体轴承结构尺寸如下：轴径为25 mm，材料为铝合金；轴瓦厚度为2 mm，宽为30 mm，内半径为15 mm，材料为3Cr13;半径间隙为0.02 mm，支点圆半径为12.5 mm。

下文将分别计算离心力造成的轴的径向变形、轴瓦和轴的热变形、轴瓦的弹性变形以及轴承偏斜和表面粗糙度对气膜厚度的影响。

3.1 离心力变形

转子在旋转时由于离心力的存在，会造成轴的径向变形，变形量为[3]

(3)

C0=[(3+ν)/8]ρω2(d2+R2)；C1=-[(3+ν)/8]ρω2d2R2；E=72 GPa；ν=0.33；ρ=2 820 kg/m3。

由(3)式可知，离心力变形量与转速的平方成正比，且和转子半径的立方有很大相关性，因此转子的转速和直径也是可倾瓦轴承设计中需要考虑的因素。对于转速较低的场合，可以忽略离心力导致的变形，但在高转速下，离心力导致的变形不可忽略。

对于直径为25 mm的轴，当转速为12×104r/min时，离心力变形为0.5 μm；转速为20×104r/min时，离心力变形为1.67 μm。由此可知，一般情况下，转速对轴离心力变形的影响可以忽略。

为了减轻轴的质量，提高轴承承载力，有时会采用空心轴。假设有2个空心轴，内径分别为15 mm和20 mm，外径均为25 mm。转速为12×104r/min时，离心力变形分别为1.1 μm和1.47 μm；转速为20×104r/min时，离心力变形分别为3 μm和4.1 μm。由此可知，虽然空心轴可以减小轴的质量，但是会导致轴的离心力变形量增大。因此采用空心轴时，需要充分考虑轴承结构尺寸对其离心力变形的影响。

3.2 热变形[4]

可倾瓦气体轴承在运行时，气膜受到摩擦而造成温升，一般情况下，这些热量会通过轴和轴瓦传递到周围环境中并且会随着轴的转动从气膜中排出。轴、轴瓦以及气膜的温度，与轴承的结构和转子的转速关系密切，一般是通过对气膜建立瞬态能量求解，再用瞬态导热方程计算轴和轴瓦的温度分布[5]。

假设气膜、轴瓦以及轴的温度一致，求解由于温升而导致的轴和轴瓦的热变形。轴瓦的热变形包括轴瓦的厚度变化和轴瓦曲率半径的变化，而轴的半径也会发生变化。这些变化会影响半径间隙和最小气膜厚度，从而影响轴承的性能。

(1)轴瓦的半径膨胀变形量为

δ1=αpRpΔTp，

(4)

对于3Cr13，αp=10-5/℃，Rp=15 mm；假设温差为20 ℃，可得变形量为3 μm。由此可知，温度的升高对名义半径间隙的影响较大，在可倾瓦结构设计中，应该充分考虑到运行中的温升问题。

(2)轴瓦厚度的变化量为

δ2=αpBΔTp，

(5)

对于3Cr13，αp=10-5℃，B=2 mm，假设温差为20 ℃，则变形量为0.4 μm。

(3)轴的热变形为

δ3=αpRΔTs，

(6)

对于铝合金，αp=2.45×10-5/℃，R=12.5 mm，假设温差为20 ℃，则变形量为6.1 μm。

3.3 弹性变形

对于可倾瓦油润滑轴承，由于载荷较大，在设计时需要考虑轴瓦的弹性变形。对于气体轴承，一般载荷较小，作用在轴瓦上的力较小，但为了减小轴瓦的惯性力以及支点处的摩擦力，一般情况下轴瓦的厚度较薄且质量较轻，有的甚至采用弹性轴瓦，因此在设计过程中需要考虑其弹性变形。轴瓦的简化结构如图2所示，假设支点为刚性轴承，则轴瓦的弹性变形[5]为

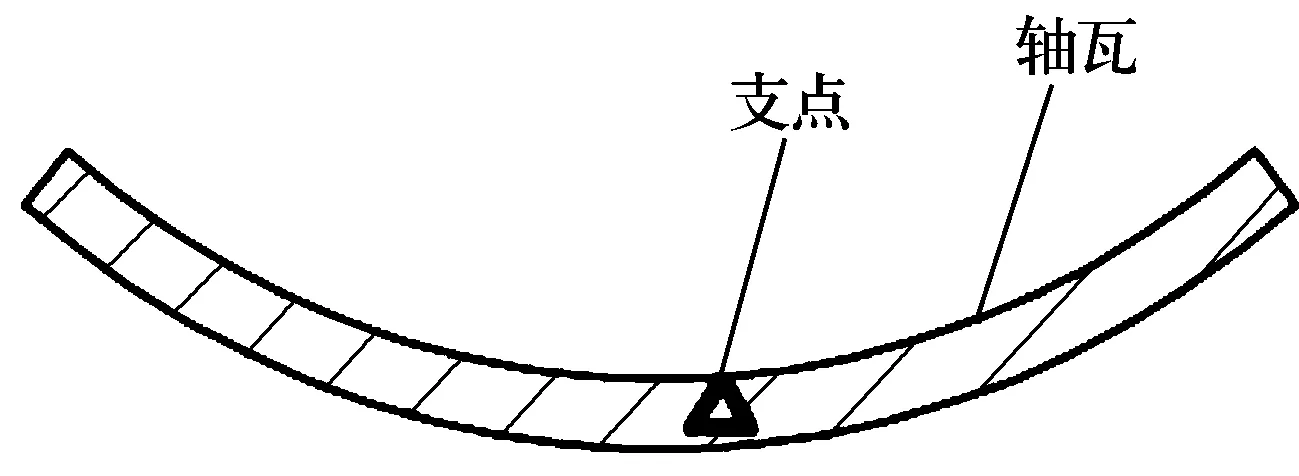
图2 轴瓦结构简图

K·δ4=F。

(7)

3.4 轴承偏斜

对于轴承-转子系统，轴承的偏斜会影响润滑膜内的压力分布、承载能力和气膜厚度等，从而影响轴承系统的稳定性。对于流体润滑轴承，即使设计非常好，由于存在制造和装配误差，转子很少能够在对中条件下运行，转子的偏斜运动常常是由制造装配误差、偏心承载、轴的热变形和弹性变形或者外部的冲击所致。由于可倾瓦分为线接触和点接触，对于线接触，轴瓦只有1个自由度，只能沿轴线摆动；对于点接触，轴瓦有2个自由度，还可以在轴向上摆动。文中分析的为线接触可倾瓦轴承。线接触可倾瓦轴承的偏斜分为2种类型：竖直偏斜和水平偏斜，通常轴承偏斜由这2种类型混合而成[6]。

z为轴承中心的轴向坐标；y为垂直于轴承中心，在竖直方向的坐标；x为垂直于轴承中心，在水平方向的坐标。

竖直偏斜：在yz平面内，轴的轴向和轴承的轴向的夹角如图3所示。

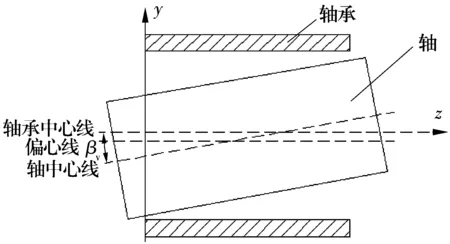
图3 竖直偏斜

水平偏斜：在xz平面内，轴的轴向和轴承的轴向的夹角如图4所示。

图4 水平偏斜

偏斜状态下滑动轴承的结构如图5所示，λ的值在0～1之间，ε0，φ，ψ详细内容可参考文献[8-9]。

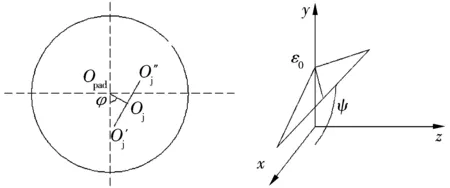
图5 偏斜滑动轴承的结构

λ=λe/λm，

(8)

cos(ψ-φ0),

(9)

λe=2βb/Cp。

(10)

3.5 表面粗糙度

在绝大多数关于可倾瓦滑动轴承的研究中，都是假设轴承-转子表面为光滑表面，然而，当表面粗糙度和润滑膜的尺寸在一个数量级时，需要考虑到润滑表面粗糙度。表面粗糙度的存在使轴和轴承的安全运行间隙减小了，更容易发生碰磨，表面粗糙度的随机模型是由Christensen提出的[9]。

润滑膜的厚度为

h=hm(x,y,z)+δ(x,y,z)，

(11)

δ(x,y,z)为轴承表面任一点的厚度与平均厚度之差，可以为正值也可以为负值。期望因子E(x)定义为

(12)

由于绝大多数的机械表面服从Gauss分布，用多项式形式随机变量的密度分布模拟Gauss分布

(13)

式中：c=3σ为随机润滑膜厚度变化的一半。考虑轴和轴承表面粗糙度，并假设两者相等，表面粗糙度使实际可安全运行的间隙减小了6σ。如标准粗糙度为0.8，则由于2个摩擦面粗糙度造成的运行间隙的减小量为4.8 μm。因此在可倾瓦轴承设计时，需要充分考虑表面粗糙度的影响。

结合(12)～(14)式，润滑膜厚度的期望值为

(14)

由此可知，表面粗糙度的存在并不影响润滑膜的平均厚度，也就是说，不会影响名义半径间隙。但是由于表面不光滑，轴承和轴在运行过程中容易发生碰磨，使安全运行的最小润滑厚度增大。另外有研究显示，表面粗糙度还会影响压力分布和承载能力等。

3.6 修正后的气膜厚度

考虑热变形、离心变形和弹性变形后气膜厚度及其变化量计算公式为

h(θ)=Cp0-(Cp0-Cb0)cos(θ-βi)-(R+

B)δisin(θ-βi)+excosθ+eysinθ+Cpλλm·

(15)

δtotal(θ)=(δ1+δ4-rg-δ3)-(δ1+δ4+

δ2)cos(θ-βi) 。

(16)

从上式可知，轴瓦的半径变化和弹性变形使气膜间隙增大；离心力变形、轴瓦厚度方向的热变形以及轴的热变形使气膜间隙减小；表面粗糙度和轴承的偏斜使安全运行的最小间隙增大，并且气膜在轴向上的厚度分布也是变化的。因此在可倾瓦的设计中，要综合考虑到各种影响因素。把影响轴承性能的主要因素控制在合理的范围以内是可倾瓦设计的关键点之一。

4 结论

相对于固定瓦轴承，可倾瓦轴承的设计制造难度较高，在不同运行条件下，对可倾瓦的结构尺寸的变化进行分析，得出如下结论：

(1)在转速不高且为实心轴的情况下，轴半径对离心力变形的影响较小，但是对于空心轴，需要考虑轴承结构尺寸对离心力变形的影响。

(2)温度的升高对轴瓦厚度的影响较小，而对轴瓦的名义半径和轴半径的影响较大。

(3)通常情况下，可倾瓦气体轴承承载力小，轴瓦的弹性变形可以忽略，但是对于弹性轴瓦，需要考虑其弹性变形。

(4)轴承的偏斜使气膜厚度在轴向上不再是一个定值，并且会影响轴承的安全运行。

(5)表面粗糙度的存在并不影响润滑膜的平均厚度，但是会使安全运行的最小气膜厚度增大。