随机数组统计偏差对Weibull分布参数估计的影响

王桂金

(原钢铁研究总院，北京 100081)

1 均布于(0，1)随机数的统计量

理想均匀分布于(0，1)的随机数组具有如下统计量[1]：

均值(MEAN)μ0=0.5；

标准差(STDEV)σ0=0.288 68;

斜度 (SKEW)γ10=0.0;

过剩峭度(KURT)γ20=-1.2。

然而，在(0，1)准均匀分布的1组随机数组的统计量很难严格符合上述要求，存在如下偏差：

均值偏差δ(μ)=μ1-μ0;

标准差偏差δ(σ)=σ1-σ0;

斜度偏差δ(γ1)=γ11-γ10；

过剩峭度偏差δ(γ2)=γ21-γ20,

其中，下角标1为准随机数组的统计量。根据文献[2],随机数α对应的Weibull随机寿命L为

L=λ0{ln(α)}1/κ0，

(1)

下文中模拟形状参数κ0和尺寸参数λ0均设为1。

2 参数κ和λ的计算

按(1)式产生的随机寿命组L，可用极大似然法(MLE)通过下式迭代计算获得该数组的实际Weibull分布形状参数κ和尺寸参数λ。

(2)

(3)

式中：N为样本数。为保证结果的可靠性，计算进行到(2)式左侧绝对值小于10-5后停止。从文献[3]中取得28组(0，1)准均匀随机数组，每组100个数据，各随机数组的统计量及其随机寿命的实际极大似然法Weibull参数κ和λ见表1。

表1 28组(0,1) 准均匀随机数组的统计量及其参数κ和λ

3 κ和λ的最小二乘法拟合

令随机寿命数组的实际形状参数κ和尺寸参数λ偏离期望值为

δ(κ)=κ-κ0;

δ(λ)=λ-λ0。

(4)

假定拟合的δ(κ1)和δ(λ1)分别为准随机数组4个统计量偏差的线性函数,则

δ(m1)=a0+a1δ(μ)+a2δ(σ)+a3δ(γ1)+a4δ(γ2);m1=κ1,λ1，

(5)

于是应用最小二乘法得

min{∑i[δ(m1)i-δ(m)i]2};i=1～28,m=κ,λ,

(6)

式中：δ(m)为随机寿命实际Weibull参数偏离值，可分别得到δ(m1)的最佳系数a0,a1,a2,a3和a4。实际上，δ(μ),δ(σ),δ(γ1)和δ(γ2)分别与随机参数分布的1～4次矩有关。

3.1 形状参数κ的最小二乘法(LSD)拟合

经过运算，这28组随机寿命拟合δ(κ1)的结果为

δ(κ1)=0.012 8-0.345δ(μ)-6.95δ(σ)+0.276δ(γ1)-0.287δ(γ2),

(7)

min{∑i[δ(κ1)i-δ(κ)i]2}=0.017 329,i=1～28。

最大和最小的绝对偏差为

max|δ(κ1)i-δ(κ)|=0.077 964，

min|δ(κ1)i-δ(κ)|=0.001 320。

最小二乘法拟合的形状参数κ1和随机寿命数组实际参数κ相差的绝对值平均只有0.004 7，而单个数据相差的绝对值不超过0.08。κ相对期望值1的最大偏离是+0.250 39和-0.125 95(表1)。因此用准随机数组的4个统计量偏差可以恰当描述κ围绕期望值的分布规律。把κ的偏差δ(κ)由小到大排列，再把拟合曲线的结果，即最小二乘法拟合形状参数偏离值δ(κ1)画在图1中，可以看出拟合结果令人满意。

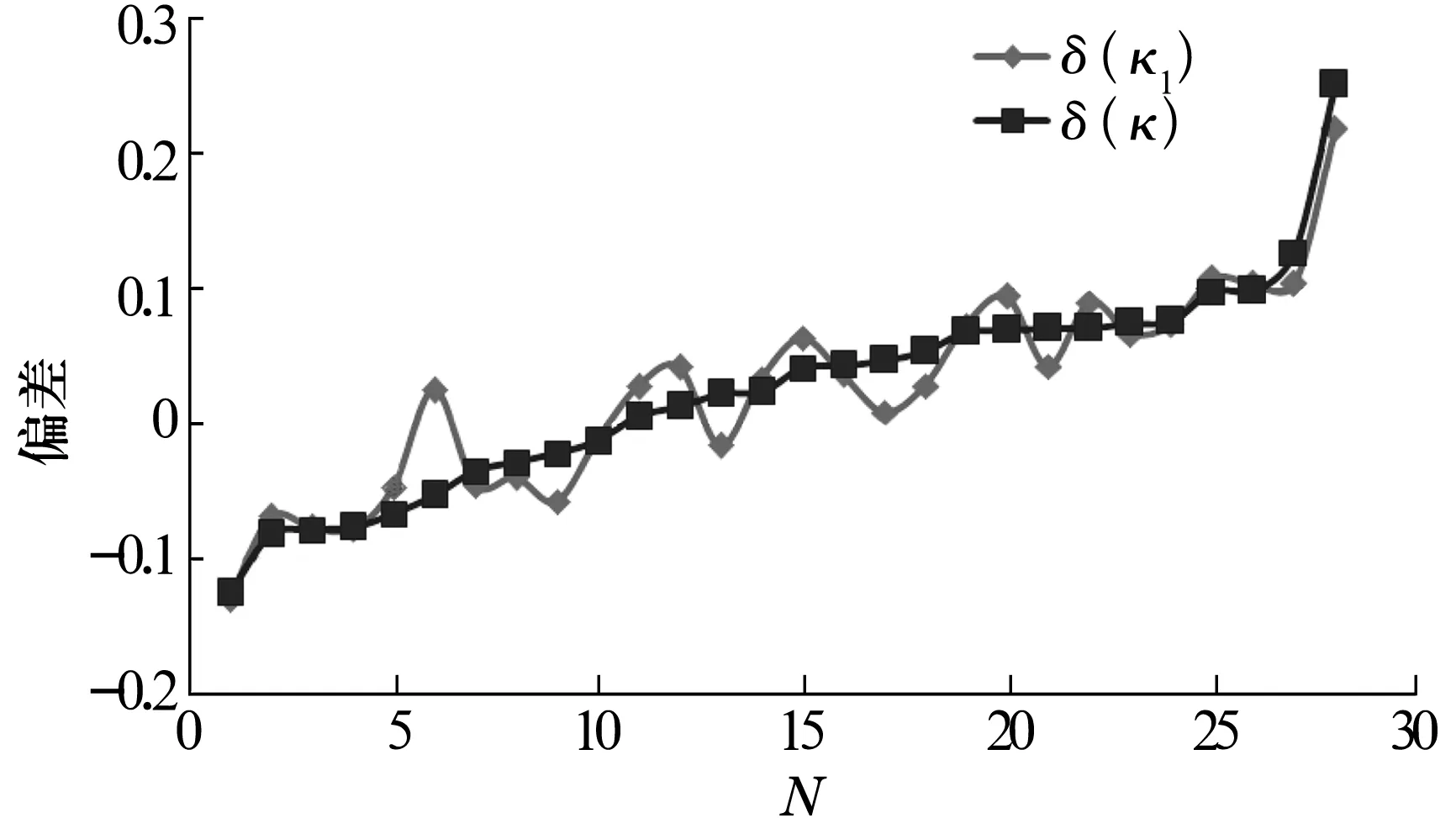
图1 28组δ(κ)与δ(κ1)值的比较

3.2 尺寸参数λ的最小二乘法拟合

经过运算，这28组随机寿命拟合δ(λ1)的结果为

δ(λ1)=-0.002 4-3.485δ(μ)+

2.23δ(σ)-0.033δ(γ1)+0.165 5δ(γ2),

(8)

min{∑i[δ(λ1)i-δ(λ)i]2}=0.005 108,i=1～28。

最大和最小的绝对偏差为

max|δ(λ1)i-δ(λ)|=0.035 44,

min|δ(λ1)i-δ(λ)|=2.78×10-5。

最小二乘法得到的尺寸参数λ1和随机数组实际参数λ平均仅相差0.002 6，而单个数据和随机寿命的实际值相差不超过0.036。λ偏离期望值1的范围是0.276 640～-0.273 886，因此，用准随机数组的4个统计量偏差同样可以恰当描述λ围绕期望值的分布规律。把λ的偏差δ(λ)由小到大排列，再把拟合曲线的结果δ(λ1)画在图2中，可以看出拟合结果更令人满意。

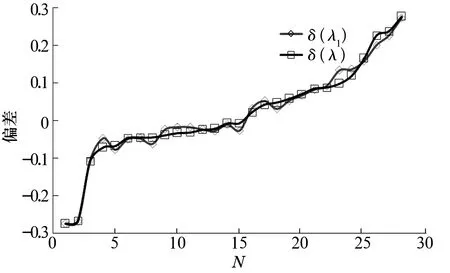
图2 28组δ(λ)与δ(λ1)的比较

4 由试验数据产生的(0，1)随机数组

(1)式的另一个重要应用是可以从疲劳寿命试验数据产生与之相关的(0，1)准随机数组。为此对文献 [4] 中提到的 1208K+H208，6104, 7208和6307轴承[5-7]进行了计算。作为例子，图3给出H208轴承37个疲劳数据对应的准随机数分布，其曲线接近于1条直线, 即接近于均匀分布(0，1)。为便于比较，表3同时列出这4种轴承随机数分布统计量偏差，并代入(6)和(7) 式估计Weibull参数κ和λ的修正量。结果表明，修正后的额定寿命L10均降低，可以接受。

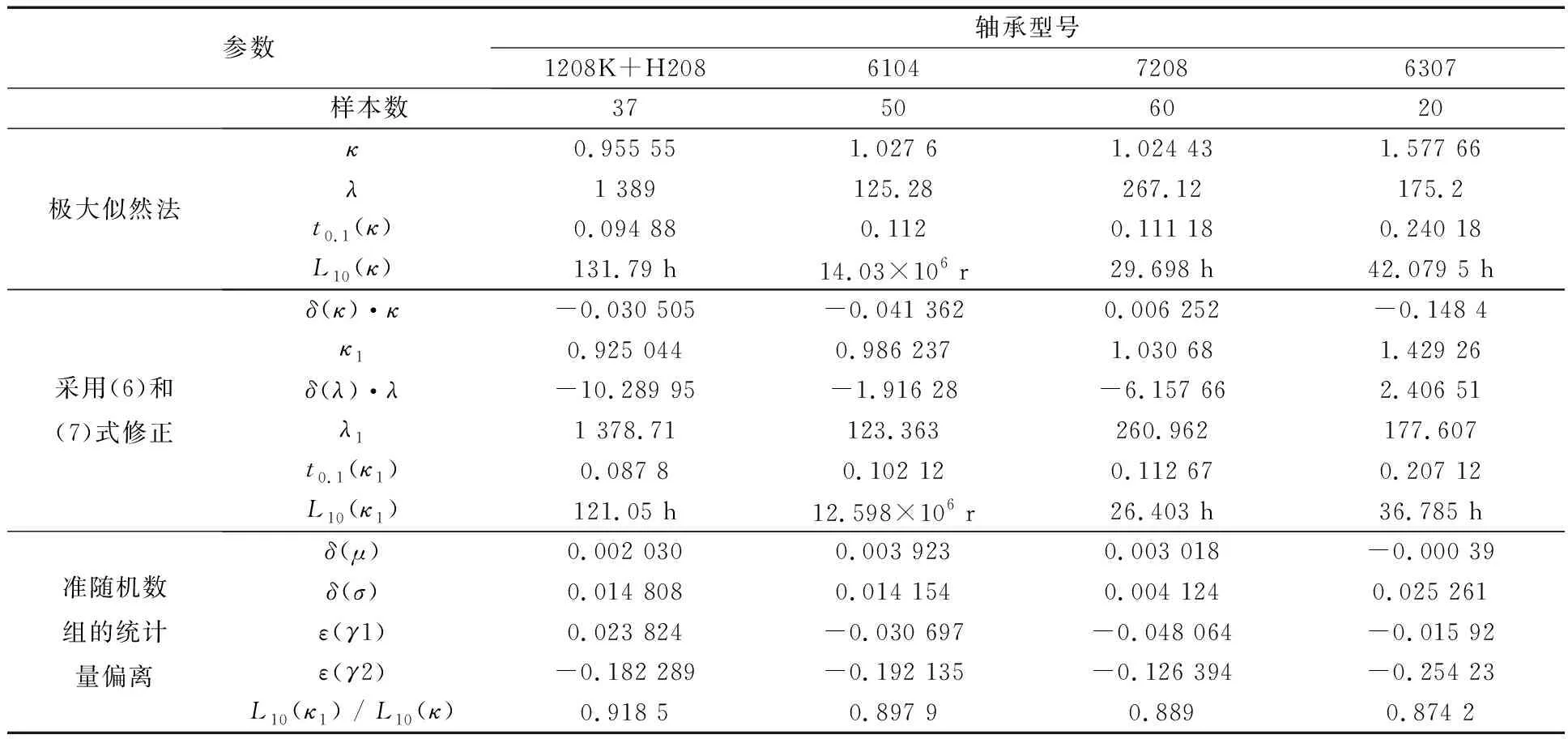
表3 4种轴承额定疲劳寿命L10的修正

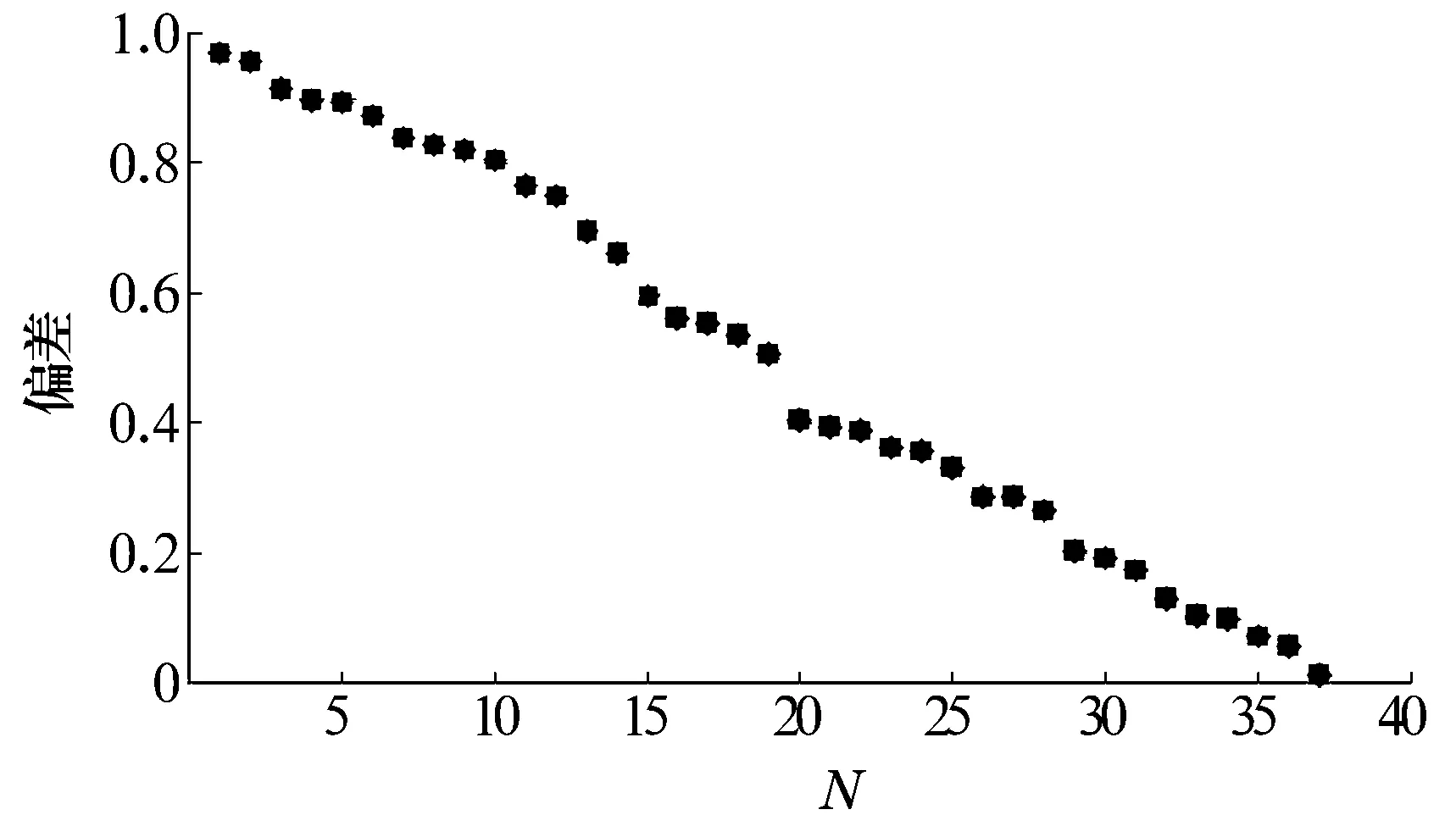
图3 1208K+H208轴承疲劳寿命对应的(0， 1)准随机数序列

5 结论

(1)当Weibull分布形状参数κ和尺寸参数λ已知，用最大似然法重新计算28组随机数组(每组100个数据)的κ和λ，所得平均值很接近设定值，同时与文献[8-9]的结果相吻合。

(2)各随机寿命数组的Weibull参数κ和λ实际值相对设定值的偏差取决于随机数组统计量(均值、标准差、斜度和过剩峭度)偏离期望值的程度，并且可以合理表达为这4个统计量偏差δ(μ),δ(σ),δ(γ1)和δ(γ2)的四元一次线性方程。这4个系数可由最小二乘法迭代计算求得。

(3) 从疲劳试验寿命数据组可以计算出其相应(0，1)准均匀分布的随机数组，该数组的统计量可以反映出寿命数据的随机特性，并可以对最大似然法计算出的Weibull分布参数κ和λ进行修正。