广义GHZ态实现的可控密集编码
闫红叶
(山西大同大学物理与电子科学学院,山西 大同 037009)
量子纠缠[1]在量子信息学中扮演着重要的角色,被广泛应用到量子隐形传态[2]、量子密集编码[3]、量子密钥分配[4]等领域。1992年Bennett等[5]提出了利用EPR对通过纠缠通道实现发送一个量子位,传送两个比特经典信息的量子密集编码方案,自此量子密集编码在理论和实验上都取得了很大进展。在Bennett等提出的标准量子密集编码方案中,密集编码的成功率可达100%。但在实际应用中由于量子态和周围环境的耦合是不可避免的,所以,这些最大纠缠态在制备过程中会受到上述及其它因素的影响而很难得到,最终粒子对会处于部分纠缠态(或非最大纠缠态)[6]。因此运用部分纠缠态作为量子通道具有很强的实际意义。在本文中,提出了利用一种利用广义GHZ态[7]作为量子信道,在第三方控制下,通过引入辅助粒子并实施幺正操作以一定几率实现的密集编码方案。
1 可控密集编码方案
假设信息的发送者Alice,接收者Bob和控制者Cliff所处的量子通道为广义GHZ态,形式如下:
|ψ>123=a|000>123+b|110>123+c|111>123, (1)
这里,粒子1,粒子2和粒子3分别被Alice、Bob和Cliff所拥有,a、b、c都是实数,且a2+b2+c2=1,假设a<b且 a<c。
为了能够很好的控制A、B之间的量子通道以及A传递给B的信息数量,C需要在基|+>3和|->3下对粒子3进行Von Neumann测量[8],然后将他测得的结果通过经典通道告诉A和B,如下:

那么广义GHZ态在基|+>3和|->3下就转化成:

由(4)和(5)可以看出,C的测量结果|+>3或|->3,粒子1和粒子2构成的态塌缩到|α>12的几率是a2sin2θ+(bsinθ+ccosθ)2或塌缩到|β>12的几率是a2cos2θ+(csinθ-bcosθ)2,由于|α>12和|β>12是非最大纠缠的,所以用它们实现的密集编码方案的成功几率小于1,且这种方案是需要C通过测量θ才能实现的,下面就来介绍实现方案:
先分析第一种情况,假设C这时测量的结果是|+>3,那么粒子1和粒子2就塌缩到|α>12。当A接收到信息后,引入一个辅助粒子|0>aux,并且在基{|0>aux|0>1,|0>aux|1>1,|1>aux|0>1,|1>aux|1>1}下,对辅助粒子和粒子1实施幺正操作:

那么总的幺正操作U1⊗I2就会把态|0>aux⊗|α>12转化成:
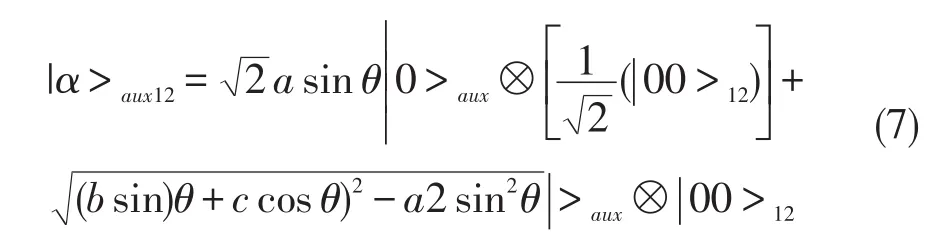
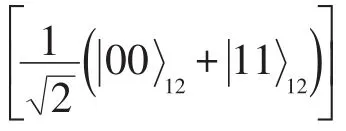

对于第二种情况,假设C的测量结果是|->3,测量方法和第一种情况基本类似,粒子1和粒子2构成的态塌缩到|β>12,但这时,情况较第一种复杂些,A必须根据θ和系数a、b、c的大小实施相应的幺正操作,有两种情况:
(a)当acosθ≥csinθ-bcosθ,B得到的平均信息是:
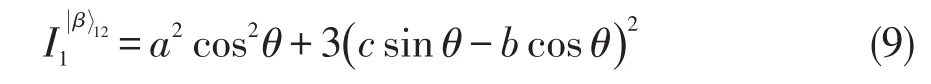
(b)当acosθ≤csinθ-bcosθ,B得到的平均信息是:

2 总结
从上面计算可以看出,广义GHZ态实现的密集编码方案中,A传递给B的平均信息量,不仅仅和C测得的结果|+>3和|->3有关,还与角度θ以及系数a、b、c的大小有关,在整个方案中,C通过控制A、B之间的信息通道,很好的把信息传递给B。
[1]SchrÄodingerE.Diegegenwarige situationinderquanenmechannik[J],Naturwissenschaften,1935,23(49):807-849.
[2]Bouwrneester D,Pan J W,Mattle K,et al.Experimental quantum telepotation[J].Nature,1997,390:575.
[3]Bennett C H,Wiesner S J.Communication via one-and two-particle operatorson Einstein-Podolsky-Rosen states[J],Phys Rev Lett,1992,69:2881.
[4]Bennett C H,Brassard G.proceedings of the IEEE International Conference on Computers[J],Systems and Signal Pro-ceeding,1984,175.
[5]Bennett C H,Wiesner S J.Communication via one-and two-par-ticle operators on Einstein-Podolsky-Rosen states[J].Phys Rev Lett,1992,69:2881-2884.
[6]Dfir W,Vidal G,Cirac J I.Three qubits can be entangled in two inequivalent ways[J].Phys Rev A,2000,62:062314-1-12.
[7]Cereceda J L.Quantum dense coding using three qubits[J/OL].Quantum Physics,2001,21.
[8]张永德.量子信息物理原理[M].北京:科学出版社,2006.
[9]Kim Y H,Kulik S P,Shih Y.Quantum teleportation of a polarization state with a complete Bell state measurement[J].Phys Rev Lett.2001,86(7):1370-1373.

