基于Hilbert空间熵的风力发电机轴承故障诊断
孙鲜明,陈长征,周昊
(沈阳工业大学 机械工程学院,沈阳 110870)
风力发电机通常需要在80 m左右的高空中常年持续运行,受外部环境影响,其工况非常复杂[1-2]。为了减小风力发电机运行维护成本、增强维修的计划性和针对性,有必要对不同工况下风力发电机的振动信号进行研究。然而,现有的风力发电机故障诊断研究多集中于非线性算法。文献[3]应用EMD对风力发电机高速轴承信号进行预处理,并在Hilbert包络谱分析的基础上提取故障频率处的幅值作为特征量,用散度指标描述故障类型和严重程度。文献[4]针对风力发电机主轴承提出了基于固有时间尺度分解和最小二乘支持向量机的故障诊断方法。文献[5]利用Fourier变换、小波变换和小波包变换分别对实验室模拟的风力发电机振动信号进行分析,提出了不同类型振动信号特征向量的提取方法。文献[6]利用小波多重分形理论对风力发电机主轴承故障进行了研究,文献[7]将Hilbert-Huang变换引入风力发电机主轴轴承故障诊断,均取得了较好的效果。
上述研究均没有考虑风速变化对风力发电机振动的影响。实际中,风速往往会引起异常振动,从而造成对故障的误判。在此,针对故障率较高的风力发电机轴承,建立基于HHT时频变换的信息熵——Hilbert空间熵,描述不同风速条件下风力发电机轴承的振动信号,利用信息熵对系统状态变化敏感时能量变化不敏感的特点,对不同风速条件下的风力发电机轴承故障进行识别。
1 Hilbert-Huang变换
1.1 经验模式分解
经验模式分解可以将信号分解成为单频率成分的函数,即IMF。IMF需满足2个条件:(1)在整个数据长度,极值和过零点数目必须相等或最多相差一个;(2)在任意数据点,局部最大值包络和局部最小值包络的平均必须为零。经验模式分解的过程如下:
(1)提取原信号的极大值和极小值。
(2)采用3次样条曲线连接极大值和极小值,形成上下包络,计上下包络均值为m1。
(3)用原信号x(t)减去包络均值得
h1=x(t)-m1。
(1)
(4)将h1作为原始数据,按照(1)~(3)步进行k次平滑,直至h1k满足IMF的条件,得到第1个IMF,记为
c1=h1k=h1(k-1)-m1k。
(2)
(5)将c1从原始数据中分离,得余项
r1=x(t)-h1k。
(3)
(6)将得到的余项r1作为原始数据,重复(1)~(5)步,直至余项rn小于给定值或成为单调函数,分解过程结束。rn代表信号的趋势,将所有IMF分量和趋势项rn叠加可得原信号,即
(4)
1.2 Hilbert变换
对于任意时间序列u(t),其Hilbert变换v(t)可定义为
(5)
式中:P为柯西主值,通常取P=1。通过上述定义,可得到信号u(t)的解析信号z(t)为
z(t)=u(t)+jv(t)=a(t)ejφ(t),
(6)
(7)
(8)
式中:a(t)为信号u(t)的瞬时幅值,反映信号能量随时间的变化情况;φ(t)为信号u(t)的瞬时相位。
根据 (1)~(3) 式对得到的IMF进行Hilbert变换,可将原信号x(t)表示为
(9)
因此,将时间t、频率ωk、幅值ak表示在一个三维图中即可得到信号的Hilbert幅值谱。
2 HHT特征熵
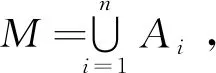
(10)
基于信息融合思想,从时频域的角度描述信号的信息熵特征,则基于HHT可提出一种HHT特征熵。HHT时频谱实质是反映时间t、瞬时频率ωk、瞬时幅值ak之间关系的图谱,因此可将ak看作(t,ωk)空间上的能量密度函数,直接反映(t,ωk)空间上的能量分布情况,由此可以在HHT空间上定义反映能量分布不确定性的HHT特征熵。
设A=ak是(t,ωk)平面上的能量分布矩阵,对矩阵A进行奇异值分解,设δ1≥δ2≥…≥δn为矩阵A的奇异值,则(t,ωk)空间上的特征谱熵为
(11)
第i个奇异值占整个特征谱的比例为
(12)
HHT特征熵继承了HHT在分析非线性、非平稳信号方面的优良性质,又量化地反映了信号在时频空间上能量分布的不确定性,熵值越高,信号的能量分布越分散,复杂程度越高。当设备无故障时,同一工况下的HHT特征熵值是恒定的,当设备出现故障时,设备的振动信号复杂性、不确定性增高,HHT特征熵值随之增高,因此可用于设备故障诊断。
3 故障诊断实例
3.1 考虑风速的轴承振动模型
风速对风力发电机组振动的影响主要有2个方面:(1)作为风电机组的驱动力,风速的变化直接影响风电机组的输入转频,并对机组各元件产生类似调频的作用;(2)作为外部激励,风速的变化能通过传动链和机舱对风电机组各元件产生直接和间接的冲击作用。因此,风速对风电机组振动的影响不同于一般设备升降速、转速波动等变化过程对设备振动的影响。考虑风速的作用不失一般性,风力发电机组轴承的振动信号模型可简化为
(13)
式中:Ai为信号第i次冲击的幅值分量;s(θ)为每次冲击响应产生的信号;θ为瞬时相位;Θ为平均周期;τi为由制造误差或局部故障引起的第i次冲击相对于平均周期Θ的微小波动;ωi为风速变化引起的第i次冲击相对于平均周期Θ的微小波动;Am为谐波幅值;fr为平均转频;Δfi为风速引起的输入转频波动;t为时间;q(θ)为轴承故障产生的谐波信号;φm为谐波相位;CA为冲击信号的幅值;pA为调频信号幅值;ΦA为调频信号相位;B为冲击信号幅值;fn为轴承特征频率;Φμ为冲击信号相位。
由于Δfi的存在,导致正常轴承在风速较高的情况下也会产生类似故障的振动,在时频谱上表现为边频和冲击。因此仅依靠时频分析难以判断异常振动是由于阵风还是故障引起。
3.2 阵风工况下的轴承故障分析
采用内蒙古朱日和地区某风场D70型风力发电机组2012年9月的在线检测数据对上述方法进行验证,数据采集现场如图1所示。试验轴承为61824型绝缘深沟球轴承,内圈固定,外圈旋转,外径为150 mm,内径为120 mm。轴承故障是由于长期润滑不良导致的严重摩擦损伤。

(a)正常轴承 (b)故障轴承
不同输入转频下正常轴承和故障轴承振动信号的HHT时频谱分别如图2、图3所示。当输入转频为0.2 Hz时,正常轴承和故障轴承的HHT时频谱差异较明显;当输入转频为0.3 Hz时,正常轴承的HHT时频谱中也包含了非常丰富的冲击成分,与故障轴承的HHT时频谱极为相似;可见当风速较高时,依靠HHT时频谱难以判断轴承异常振动的原因。

图2 正常轴承的HHT时频谱

图3 故障轴承的HHT时频谱
为解决该问题,采用Hilbert空间熵对故障轴承不同输入转频下的振动信号进行分析,并在相同条件下与同型号风机正常轴承的振动信号进行对比,结果如图4所示。

图4 不同输入转频下的轴承Hilbert空间熵值曲线
当轴承处于正常状态时,其熵值在4.4~4.6之间,而当轴承处于故障状态时,其熵值在5.0~5.2之间。可见,故障轴承的Hilbert空间熵值远高于正常轴承。随着输入转频的增加,二者的熵值均有增大的趋势,但变化不明显,这是由于Hilbert空间熵主要反映信号的不确定性和复杂性,对故障较为敏感,对转频变化则不敏感。此外,熵值随转频的增加并非是线性的,因为风速变化除了直接影响转频变化,还使加载在风机上的扰力变化,而这部分变化随机性较大。
与HHT等时频变换方法相比,Hilbert空间熵更简单、更直观,且受风速变化的影响较小,从而减少了由于风速变化导致的对风力发电机故障的误判,更适合作为风力发电机轴承故障诊断及在线监测的指标。
4 结论
(1)从信息论的角度,针对风力发电机轴承故障问题,提出了Hilbert空间熵方法,通过对D70型风力发电机故障轴承的分析,证明Hilbert空间熵能够直观、有效地显示信号的复杂性和不确定性,可以作为故障诊断的指标和依据。
(2)通过对不同风速下风力发电机轴承故障的分析,证明Hilbert空间熵对于风速变化不敏感,对于轴承故障很敏感,在风速不断变化的条件下,能有效诊断风力发电机轴承故障,因此将Hilbert空间熵作为风力发电机故障诊断的指标,可以有效避免由于风速变化引起的异常振动而造成的故障误判问题。

