PCA和自相关包络分析在转盘轴承故障诊断中的应用

杨杰，陈捷，洪荣晶，封杨

(南京工业大学 机械与动力工程学院，南京 210009)

转盘轴承作为大型旋转机械的一种关键部件，广泛应用于风力发电、工程机械、港口机械、海洋平台和军用装备等领域[1]。转盘轴承不同于普通轴承，能同时承受轴向力、径向力和倾覆力矩。由于其使用寿命具有较大的离散性，若定期更换可能会得不到充分利用，造成浪费；若定期检修，则可能在检修前已经发生故障。转盘轴承的低速重载特性导致其振动信号较微弱，因此，进行状态监测和故障诊断具有较大难度。

在许多机械故障监测或诊断过程中只需判断设备的工作状态，诊断出故障再进一步分析处理。前期的机械故障监测可看作机械设备正常和异常状态的分类问题，目前国内外学者对轴承状态实时监测和早期故障诊断方法已进行了大量研究。文献[2]提出了大型转盘轴承的信号处理方法。文献[3]有针对性地概括了基于振动信号、温度信号、摩擦力矩、声发射和应力波的转盘轴承监测诊断技术，并对比分析了上述信号处理方法。文献[4]综合了转盘轴承的温度、摩擦力矩及加速度信号的曲线发展趋势对轴承进行故障诊断。文献[5]采用主元分析(Principal Component Analysis ，PCA)对火电厂送粉风机轴承进行故障监测和诊断。文献[6]采用PCA对轴承故障状态进行监测。文献[7]提出了一种总体经验模式分解(Ensemble Empirical Mode Decomposition，EEMD)和PCA相结合的多元多尺度转盘轴承故障诊断方法。文献[8]提出了一种小波分析方法，再结合PCA算法监测故障过程。文献[9]提出了一种经验模式分解(Empirical Mode Decomposition，EMD)和PCA相结合的轴承故障源盲分离方法。文献[10]采用小波分析将信号分解到不同的时间尺度上，然后利用PCA监测机械设备运行的全过程。文献[11]研究了T2和预测误差平方(Square Prediction Error,SPE)统计量下的故障重构和诊断问题。综上所述，由于低速重载的转盘轴承振动信号微弱，在早期诊断方面研究甚少，下文采用自相关降噪和PCA相结合进行早期故障诊断。

1 时延自相关降噪特性分析

出现局部故障的转盘轴承将产生一种周期性冲击信号，但采集到的振动信号经常被外界噪声干扰(即周期信号和随机信号的叠加)，导致其故障特征信息不明显。然而，自相关分析是一种能够提取信号中周期成分而不受外界噪声影响的方法。自相关函数描述同一信号在不同时刻的相互关系，定义为

(1)

式中：T为信号周期；τ为时延。

根据自相关特性[12]，随机信号的自相关为0，周期信号的自相关仍为周期信号。因此，可将自相关函数应用于转盘轴承振动信号降噪，保留振动信号中的有用成分，去除随机性的非周期噪声干扰。

2 PCA

2.1 基本原理

PCA是一种典型的数据统计分析理论，其思想最先由Pearson K[7]提出，经Hotelling H进一步研究后建立了一套数学理论准则，使其成为一种判别随机变量的独立方法。PCA主要对现场采集的测量数据进行统计建模，然后把数据从高维空间投影到能准确表征过程状态的低维空间统计模型中，所得到较少数目的特征变量能更集中地反映原来变量所包含的变化信息，摒弃冗余信息，实现过程故障的监控和诊断。

2.2 模型[12-13]

对于数据矩阵X∈RI×J，每一行Xi对应一个观测样本，每一列Xj对应一个变量。为了减小环境、测试系统及信号复杂性对数据的影响，使信号具有客观且统一的标准，常采用标准化的方法对数据进行预处理，即

(2)

式中：Xi为待处理的标准化数据；E(X)为待标准化处理的数据均值；σ为待标准化处理的数据方差。这样原始数据就化为均值为0且方差为1的标准数据。对标准化的数据矩阵X′进行PCA后，X′分解为2个部分，即

(3)

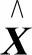
(4)

式中：λ为对角阵，由X′的协方差矩阵的前k个特征值构成。

(5)

式中：n为样本数；α为置信水平；Fk,n-k,α为带有k和n-k个自由度、置信水平为α的F分布临界值。

根据PCA残差空间判定准则，在正常工况下应满足SPE≤SPElim，对于第i个采样点的SPE为

(6)

式中：ei为建模误差矩阵E的第i行；I为单位矩阵；Pk为前k个主元的主元矩阵。当置信水平为α时，SPE统计量的阈值限SPElim为

(7)

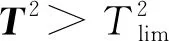
3 转盘轴承试验介绍

风电转盘轴承试验台如图1所示，可同时施加轴向力和倾覆力矩，并通过电动机驱动轴承旋转，模拟轴承实际工况，试验台测控系统原理如图2所示。转盘轴承技术参数及加速寿命试验参数分别见表1、表2。试验中途运转到30 000 r时拆机检查，然后继续运行直至破坏，共运行12天。

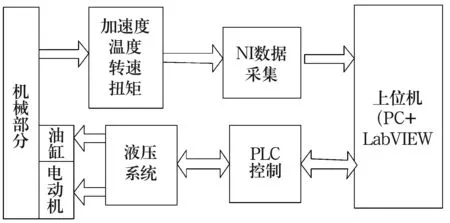
图2 转盘轴承试验台测控系统原理

表1 转盘轴承技术参数

表2 转盘轴承加速寿命试验参数

4 试验分析与故障诊断

4.1 样本数据选择

转盘轴承加速寿命试验中加速度的采样频率为2 kHz，由于采集的数据量较大，故对第1天正常样本数据等间隔选500个点为1组，取6组样本共3 000个样本数据点。由于采集的振动信号中包含大量噪声，将振动信号首先通过时延自相关方法进行降噪，然后建立正常工况下的PCA模型，将后续采集到的试验数据代入PCA模型，再利用T2和SPE统计量进行故障检测。

4.2 故障检测

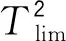
图3 第1天正常样本T2统计图

图4 第1天正常样本SPE统计图

图5 第5天样本数据T2统计图

图6 第5天样本数据SPE统计图

4.3 故障特征分析

为了准确找出转盘轴承早期故障类型，对第5天样本数据进行故障特征频率提取。根据文献[12]中的公式计算得到转盘轴承各部件的故障特征频率，见表3。

表3 转盘轴承各部件的故障特征频率 Hz

第1天和第5天样本数据自相关分析波形图分别如图7和图8所示。第1天样本数据自相关分析波形处于平稳状态，未检测到其他周期性成分出现，而第5天样本数据自相关分析波形的周期性波动明显，可能是转盘轴承早期故障所致。根据文献[14]关于轴承振动信号早期故障特征的描述和图8可推测转盘轴承早期故障特征中含有调制成分。包络分析可对调制成分进行包络解调，从而提取故障特征频率。因此，对第5天样本数据首先通过自相关进行降噪，然后将降噪后的样本数据进行Hilbert包络解调分析后再进行频谱分析。第5天样本数据自相关包络频谱分析如图9所示。图9中频率2.32 Hz与表3中转盘轴承钢球故障特征频率2.21 Hz最接近。然而，图9中的14.57 Hz频率成分并不在转盘轴承故障特征频率范围内，但是与理论计算出的转盘轴承钢球自转频率16.59 Hz较接近。以上各频率成分均通过试验数据分析得出，由于试验数据易受外界各种因素的干扰，所以提取的频率与理论值有一定偏差，因此可认为14.57 Hz为钢球自转频率，并非转盘轴承故障特征频率。

图7 第1天样本数据自相关分析波形图

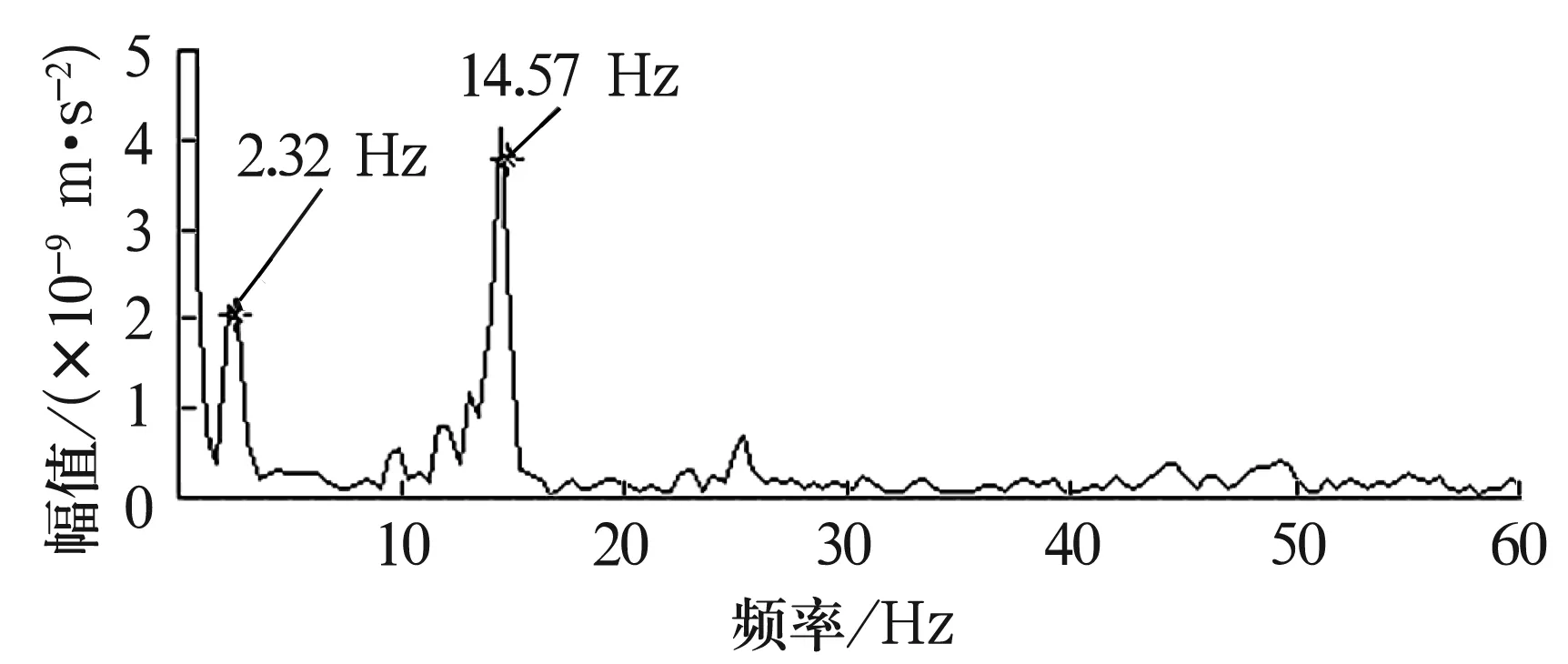
图9 第5天样本数据自相关包络频谱分析

通过以上分析可初步判定转盘轴承钢球出现了早期故障，但由于转盘轴承加速寿命试验要求在转盘轴承运转30 000 r时(即第7天)才停机拆卸观察其损坏情况，所以在第5天诊断出钢球出现故障时并未拆机检查。

为了验证此方法的有效性，对转盘轴承运行到30 000 r时的振动信号进行自相关包络频谱分析。第7天振动信号包络分析如图10所示，振动信号频谱杂乱，频率并不是集中在某几根谱线上，而是在一定范围内普遍存在，无法找出故障特征频率。为了解决该问题，对自相关函数波形进行带通滤波，对滤波后的信号再进行包络频谱分析，第7天振动信号带通滤波包络谱分析如图11所示。由图11可知，杂频分量明显减少，凸显出故障频率2.1 Hz。最后将转盘轴承拆卸后发现内、外沟道均未出现故障，但某些钢球上已出现较多的点蚀故障及微小裂纹。

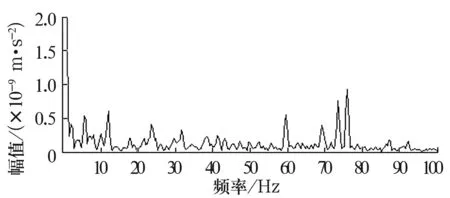
图10 第7天振动信号包络分析

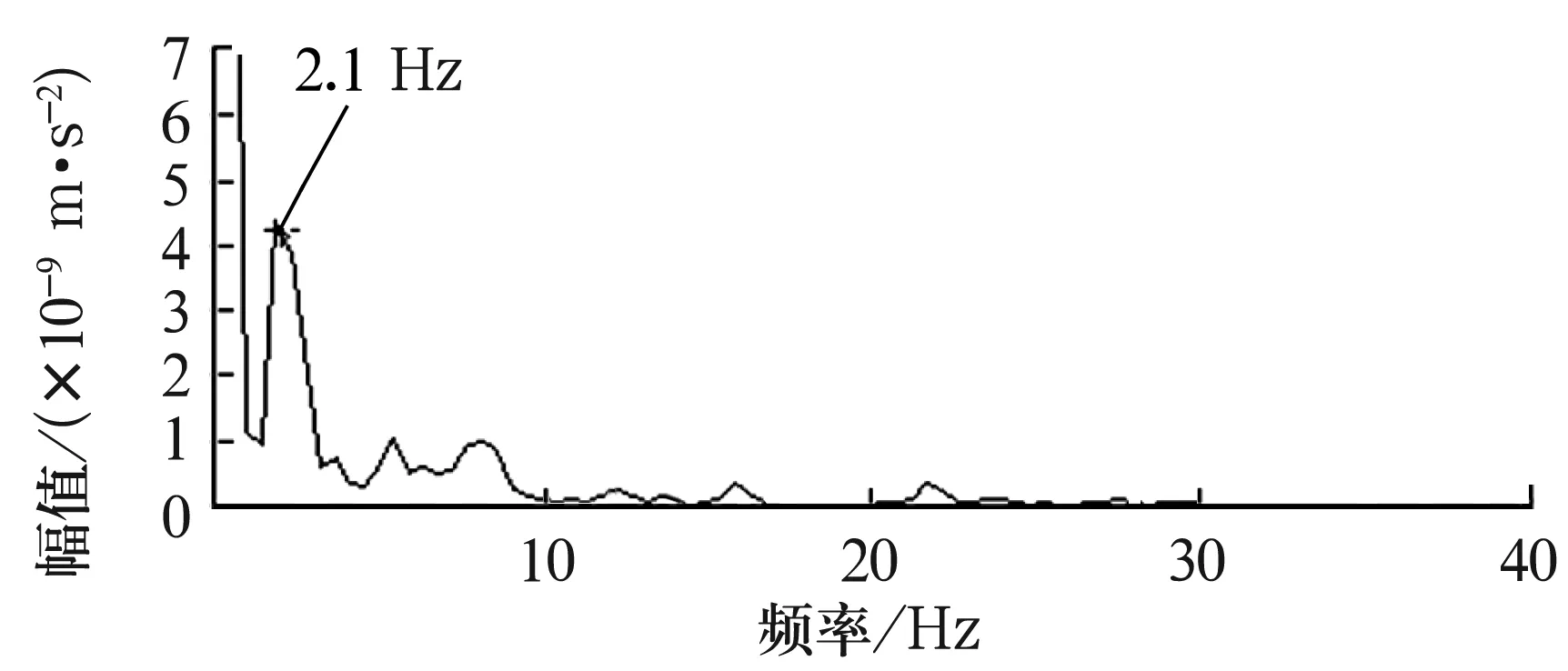
图11 第7天振动信号带通滤波包络谱分析

5 结束语

对连续运行的机械设备进行故障诊断，如果要及时发现其故障状态，并对其进行故障特征分析，传统的诊断方法往往很难实现，或者实现所花费的代价比较昂贵。PCA是一种利用统计原理对样本数据建立系统的低维模型方法，再结合T2和SPE统计量进行故障检测。试验结果表明，该方法能有效分辨出转盘轴承正常和故障状态，可较好解决转盘轴承故障数据处理问题，并且对其故障样本数据进行Hilbert包络谱分析能及时找出故障特征，说明自相关包络分析对提取转盘轴承早期故障特征频率有一定效果。