基于全局响应面法的电动汽车车架多目标优化

尹安东，曹 诚，徐俊波，龚来智

（合肥工业大学 机械与汽车工程学院，合肥 230009）

基于全局响应面法的电动汽车车架多目标优化

尹安东，曹 诚，徐俊波，龚来智

（合肥工业大学 机械与汽车工程学院，合肥 230009）

对电动汽车车架进行有限元分析，在此基础上选取车架前部、后部、副车架部分的尺寸厚度以及这三个部分的肋板的厚度作为设计变量，运用全局响应面法（Global Response Surface Method，GRSM）以一阶模态频率大于32 Hz作为约束，对车架的扭转刚度、弯曲刚度和总质量进行多目标优化，获取Pareto最优解集，给出优化备选方案和建议。

电动汽车；车架；全局响应面法；多目标优化

新能源汽车特别是电动汽车，毫无疑问将是未来汽车行业发展的方向[1]。而在电动汽车车身设计方面，很多厂商试图将传统汽车的车架运用到电动汽车上。由于电动汽车车身和车架需要承载动力电池、电机等异于传统汽车的部件载荷，在对车架进行优化时需要对此进行考虑。

在类似结构优化问题上，罗明军[2]等在对车架进行有限元分析的基础上，提出对车架薄弱部位进行加强的方案；扶原放[3]等将可靠性理论引入车架结构的优化设计，给出多工况条件下拓扑优化结果；谢然[4]在实验设计的基础上考虑多个性能指标，建立精度符合要求的响应面近似模型，运用非劣性分层遗传算法进行多目标优化。

本文采用的全局响应面法（Global Response Surface Method，GRSM）是一种直接优化方法[5]，省去实验设计以及后续单独的响应面的建立过程，在进行多目标优化的同时具有高效、实用的优点，将此方法应用于小型纯电动汽车车架各部分的厚度尺寸的优化较为合适。

1 车架有限元建模及分析

实例电动汽车车架采用铝铜合金材料，建模时以板壳单元进行模拟。对实际工况条件进行量化，将量化的工况条件定义为模型中的边界条件，并组合成不同工况[6]。一般认为，车架结构的主要问题是刚度，其次是强度[7]，如果车架结构的刚度已满足要求，则其强度基本能满足要求。车架刚度的设计准则是在指定载荷下，车架最大变形应不超过许用值。此外，还需保证车架有合理的振动特性。本文主要分析车架的弯曲工况、扭转工况和自由模态工况。

分析弯曲工况时，对照实际布置情况和CATIA模型，在HyperMesh中副车架位置以950 N的集中载荷模拟动力总成，在车架后部电池安装点以1 800 N的集中载荷模拟电池，在座椅安装点处以2 000 N的集中载荷模拟乘员质量，以重力加速度施加车架自重，以分布载荷的形式模拟车身等部件质量，分别约束前后悬架支撑点位置x，y，z三个方向的平动和转动自由度（如图1）。

分析扭转工况时，仅约束后悬架支撑点位置x，y，z三个方向的平动和转动自由度，在两前悬架支撑点处施加方向相反的大小为2 kN的垂直载荷，并约束两支撑点中点处x，y，z三个方向的平动自由度（如图2）。

利用OptiStruct求解器进行求解。为方便地对车架在特定工况下对于不同载荷的承载能力进行衡量以及与后续优化结果的对比，本文弯曲刚度KB通过车架的最大挠度ymax来衡量，最大挠度越小，则认为车架刚度越大，经计算，为4.58 mm（如图3）；扭转刚度KT通过总扭转力矩与前悬架支撑点处扭转角的比值来衡量，经计算，为3 280.3Nm/（°）（如图4）。

车架的模态特性是控制汽车常规振动性能的关键指标。对车架进行模态分析，在有限元模型的基础之上，释放全部车身载荷及所有约束频率范围时从 1 Hz 开始[8]，跳过刚体模态。从分析结果看，车架第一阶模态频率f为35.9 Hz，表现为车架前段弯曲共振（如图5）。

当汽车以一定车速v（m/s）驶过空间频率n（m-1）的路面不平度时输入的时间频率[9]为：

其共振车速为V=3.6 Lminf（km/h），其中Lmin为不同路面的不平度波长的最小值。电动汽车一般在平坦公路上行驶，这里取Lmin=1.0 m，取常用车速V为0~100 km/h，可得到路面不平度的激励频率范围约为0~28 Hz。由此可见，车架模态特性表现较好，有轻量化设计的余地。

2 基于GRSM的多目标优化

2.1 全局响应面法

响应面[10]是指通过一定次数的试验在局部范围内比较精确地逼近函数关系，并用简单的代数表达式展现出来，即假设设计目标与设计变量之间存在如下关系：

式中：y是设计目标；φ1是关于变量的函数；β1是待定系数；ε是系统误差，且ε~N（0，σ2）。

响应面方法计算简单并具有良好的鲁棒性。工程应用中一般将响应面设计成一阶或二阶的多项式，在保证非线性特征的同时，可以使响应面结构简单，降低计算成本。如完整的二次多项式模型表示如下：

式中：ai、 bi、 cij为待定系数，利用最小二乘法求得。

其中, λ为初始扰动波长, 无量纲Atwood数A=(ρh-ρl)/(ρh+ρl), ρh和ρl分别为重流体和轻流体密度. 当重流体密度远远大于轻流体密度时, 即A=1时, 非线性饱和阈值大约是扰动波长的0.1倍. 也就是说, 在Atwood数为1的情况下, 当基模的幅值达到扰动波长的1/10时, RT不稳定性就已经进入非线性阶段. 在进入非线性阶段之前, 高次谐波的作用已经不可忽视. 当基模的幅值接近扰动波长的1/10时, RT不稳定性正在经历弱非线性阶段, 高次谐波迅速增长, 和基模共同作用决定着界面的演化发展.

全局响应面法（Global Response Surface Method，GRSM）[11]是一种基于响应面的直接优化方法。这种算法从初始值周围一些随机的点开始优化，每一迭代步中，基于响应面的全局采样算法会产生额外的几个点，从而在兼顾局部搜索和全局搜索之间寻求一个较好的平衡。所有这些在一个迭代步中产生的点可并行求解，新产生的点将用来更新响应面以更好的拟合实际模型。

GRSM具有全局搜索的能力，优化过程中既可以进行单目标优化也可以进行多目标优化，可设置约束，也可进行无约束优化，应用比较灵活。优化流程图如图6。

2.2 多目标设计

考虑到电动汽车车架对于轻量化的需求以及承载特性异于普通轿车车架，同时车架模态特性需避开电动汽车常用路面不平度的激励频率，通过对车架构造以及制造工艺的分析，本文选取车架不同部位厚度尺寸作为变量，将车架质量最小，弯曲刚度和扭转刚度最大作为目标，以一阶模态频率在32 Hz以上作为约束，用全局响应面法进行多目标优化，寻求车架综合性能的提升。即建立如下优化问题：

式中：T2，T3，T5分别车架前部、副车架以及车架后部的材料厚度尺寸；T1，T4，T6分别为这三部分的肋板厚度尺寸；m为车架质量；ymax为车架弯曲工况下车架最大挠度；KT为 扭转刚度；f 为一阶模态频率。各目标值计算方法前文已有叙述。

由于多目标优化问题中的目标间是互相矛盾的，优化解不可能是单一的解，而是一个解集，称为Pareto最优解集，而对应的目标函数空间的像称为Pareto前沿。

2.3 多目标优化结果

本文综合考虑各方面因素，选取了两组pareto解作为备选优化方案，如表1所示。

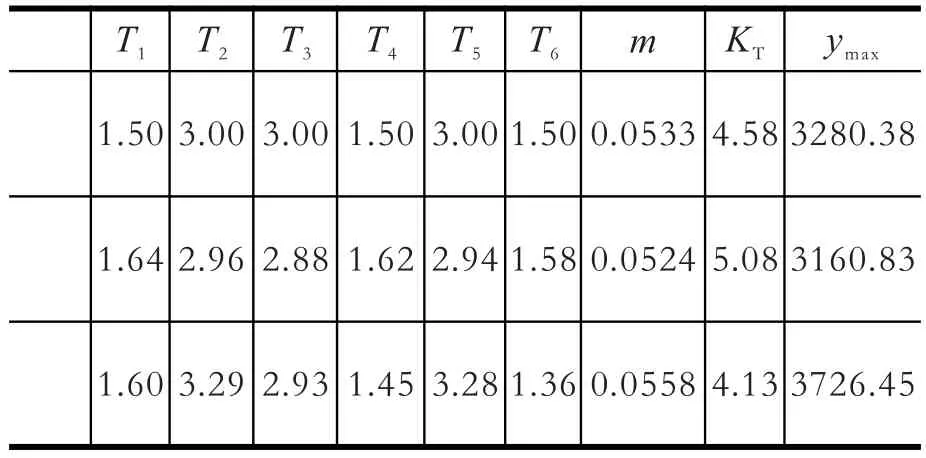
表1 优化方案比较

从表中可以看出，相比于原方案，若要倾向于轻量化需求，则可选择方案一，将参数取整后带入有限元模型中计算，结果显示质量降低1.8%；若着重提高车架的承载性能，则可选用方案二，车架本身为轻量化材料铝铜合金，质量在可接受范围内，弯曲工况下最大挠度可下降9.8%，扭转刚度可获得18.2%的提升，明显加强了承载特性。对车架优化改进时，可根据需要，在以上方案中权衡选取。

3 结语

（1）对某小型纯电动汽车车架进行有限元建模及分析，用适当的方法量化车架承载弯曲载荷和扭转载荷的能力。

（2）利用全局响应面法，求解以质量最小，弯曲载荷、扭转载荷承载能力最大为目标，一阶模态特性符合要求的多目标优化问题，得出pareto解集，并给出不同备选方案，为后续整车级别的多目标、多学科优化提供参考。

[1]陈清泉，孙逢春，祝嘉光.现代电动汽车技术[M].北京：北京理工大学出版社，2002.

[2]罗明军，王文林，徐高新.陆风X6车架有限元分析与结构优化[J].机械设计与制造，2009，8:32-34

[3]扶原放，金达锋，乔蔚炜.微型电动车车架结构优化设计方法[J].机械工程学报，2009，45(9):210-212.

[4]谢然.多目标优化方法在车身结构轻量化设计中的应用研究[D].广州：华南理工大学，2010.

[5]Raymond H.Myers.Response Surface Methodology: Process And Product Optimization Using Designed Experiments[M].Wiley.2008.

[6]Gu Zhengqi, Mi Chengji, Wang Yutao.A-type frame fatigue life estimation of a mining dump truck based on modal stress recovery method[J].Engineering Failure Analysis,2012,26:89-99.

[7]孙凌玉.车身结构轻量化设计理论、方法与工程实例[M].北京：国防工业出版社，2011.

[8]王平，郑松林，吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报，2011,2:102-108.

[9]余志生.汽车理论第4版[M].北京：机械工业出版社，2006

[10]赖宇阳.Isight参数优化理论与实例详解[M].北京:北京航空航天大学出版社，2012,10.

[11]刘孟祥，胡辽平，谢辉.基于形状变量和全局响应面法的增压器涡轮多目标优化[J].内燃机工程，2013，34（4）：71-76.

专家推荐

王 彦：

全局响应面法对多目标优化是较好的方法。电动汽车车架的刚度和模态目标值国内经验少，不易确定，希望读者能够共同探讨。

Multi-Objective Optimization of Electric Vehicle Frame Based on GRSM

YIN An-dong, CAO Cheng, XU Jun-bo, GONG Lai-zhi
(School of Mechanical and Vehicle Engineering, Hefei University of Technology, Hefei 230009, China)

Finite element analysis of an electric vehicle frame was taken, and a multi-objective optimization was implemented by global responsible surface method, in which the objectives are to maximize the torsional stiffness and the bending stiffness, minimize the total mass, the constraints are to keep the first-order natural frequency larger than 32 Hz, the design variables are the thicknesses of front frame, rear frame, the subframe and their ribs.Then the Pareto optimal solution set was obtained for optimizing choice, and the optimizing options and proposal were given.

electric vehicle; frame; GRSM; multi-objective optimization

U469.72

A

1005-2550（2014）05-0008-04

10.3969/j.issn.1005-2550.2014.05.002

2014-03-07

国家“863”节能与新能源汽车重大专项(编号：2012AA111401)资助项目；安徽省自然科学基金（编号：1208085ME78）资助项目。