外圆旋风铣削加工直线度误差分析
赵海侠,杨 文,张兴伟,王 可,孙兴伟
(1.沈阳工业大学 机械学院,辽宁 沈阳 110870;2.长春汽车工业高等专科学校,吉林 长春130013;3.东港东洋物产有限公司,辽宁 沈阳 118300)
0 引言
旋风铣削法是重点推广的高效绿色制造技术,具有生产效率高、加工面表面粗糙度值低等优点,在批量生产中具有明显的优越性。本文涉及的外圆旋风铣床主要用于加工固定直径的细长轴类零件外圆,相较于传统的车削加工方法可显著提高零件的加工效率[1]。为检验外圆旋风铣床铣削加工的细长轴类零件是否能满足加工精度要求,本文对细长轴类零件的轴线直线度误差进行了理论分析研究。
1 外圆旋风铣床运动原理
外圆旋风铣床俗称“扒皮机”,主要用于铣削固定直径细长轴类工件外圆表面,可加工直径为Φ35mm~Φ85mm、长达9 000mm的轴类零件,具有较强的刚性和稳定性,切削效率高,在批量生产中具有明显的优越性。外圆旋风铣床组成结构如图1 所示。

图1 外圆旋风铣床组成结构图
根据轴类零件材料铣削的实际情况,铣削前调节液压站节流阀控制进给速度,调节液压站调压阀控制前后跟刀架夹紧力,预防工件加工时产生滑动。铣削加工时液压缸推动上料架上的工件进给至床头前跟刀架的中间位置,前跟刀架关闭,工件锁紧后主轴电机启动,带动刀盘高速铣削,等工件运动至后跟刀架中间位置,后跟刀架闭合,工件震动减小开始平稳铣削。因液压缸推杆长度(3 000mm)不及工件长度,加工一半时液压缸后退加入接杆继续铣削完成整个加工过程。
本文主要研究外圆旋风铣削加工时工件的直线度误差。细长轴类零件轴线的直线度误差属于任意方向上的直线度误差,可用直线度最小包容区域的直径来表示[2,3],如图2 所示。通过分析机床的运动原理及影响工件直线度误差的因素,对工件在前跟刀架夹紧、铣刀切削和后跟刀架夹紧这一加工过程中弯曲变形的改变进行分析,可求得细长轴类零件加工前后直线度的变化。
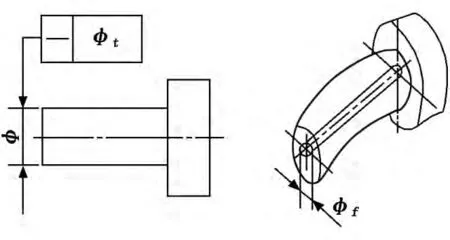
图2 任意方向上的直线度误差
2 建立直线度误差模型
细长轴类零件在机械加工过程中常常发生弯曲变形,且在很多场合表现为空间弯曲,即轴线为空间曲线。根据空间解析几何理论[4],已知空间一条曲线的方程,可以推出这条曲线关于3个坐标面的投影方程,那么可以选取两个较简单的投影方程作为这条曲线的方程,即将轴线表达平面化。数学上曲线的弯曲程度用曲率来表示,工程实际中和材料力学领域则用挠度来表示,并以挠率来描述空间曲线上某一点的相对弯曲程度。由于轴线是空间曲线且较复杂,若在直角坐标系中直接用曲率来求弯曲程度比较麻烦,但是在极坐标系中却比较容易。极径ρ表示轴线的弯曲程度,ρ越大,则在那一点处的弯曲挠度越大[5]。
因待加工细长轴类零件的材料、直径、长度和原始直线度各不相同,外圆旋风铣床对零件的铣削加工也会不同,则加工后零件的直线度变化范围也会略有差异。以前跟刀架前端面、后跟刀架后端面来分割工件的加工过程,把工件经过前跟刀架、铣刀和后跟刀架时的每一瞬态的弯曲变形曲线作为要求解的曲线解析表达式,建立相关数学模型,对工件的直线度误差进行求解,可求得外圆旋风铣床对细长轴类零件直线度误差的校正范围。以铣刀切削面为分界面,左侧曲线为待加工工件原始弯曲变形,右侧曲线则为加工后工件的弯曲变形。
为了便于求解直线度误差,我们约定:①以前、后跟刀架两端面的中心连线为z坐标轴,以铣刀切削面竖直方向为x轴,垂直xoz面方向为y轴,构成空间直角坐标系,如图3 所示,并建立曲线方程:左、右曲线上各点坐标为(xi,yi,zi)和(xj;yj;zj);②用挠度ρ、挠率φ2个参数表达曲线的弯曲,设曲线左端点(前跟刀架左端面)到xoy面连线的长度为l1,右端点(后跟刀架右端面)到xoy面连线的长度为l2,则有:
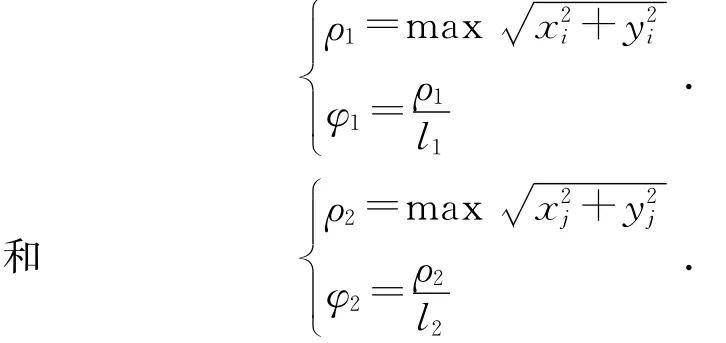
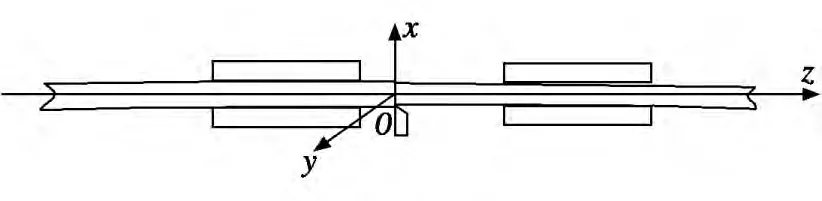
图3 建立空间直角坐标系
3 求解直线度误差
外圆旋风铣床主要是针对细长轴类圆棒料,这类轴的原始参数为轴径Φ35mm~Φ85mm、长度达9 000mm。观察外圆旋风铣床加工后的各类细长轴类零件,会发现在某一点或一段距离里,工件表面会遗留前跟刀架钳铁造成的刮痕且有深有浅,这些地方是工件弯曲程度相对较大的地方,对这些加工段进行重点分析求解,可以得出外圆旋风铣床对细长轴类零件直线度误差的校正范围。
以其中一根为例,该轴材料为45钢、长8 287 mm、直径为Φ64mm,加工后直径为Φ58mm。取该细长轴弯曲最大处轴线原始坐标数据求得轴原始挠度(见表1),与加工后轴线挠度(见表2)进行比较,得出其直线度变化值ρΔ=ρ1-ρ2=1.07mm。
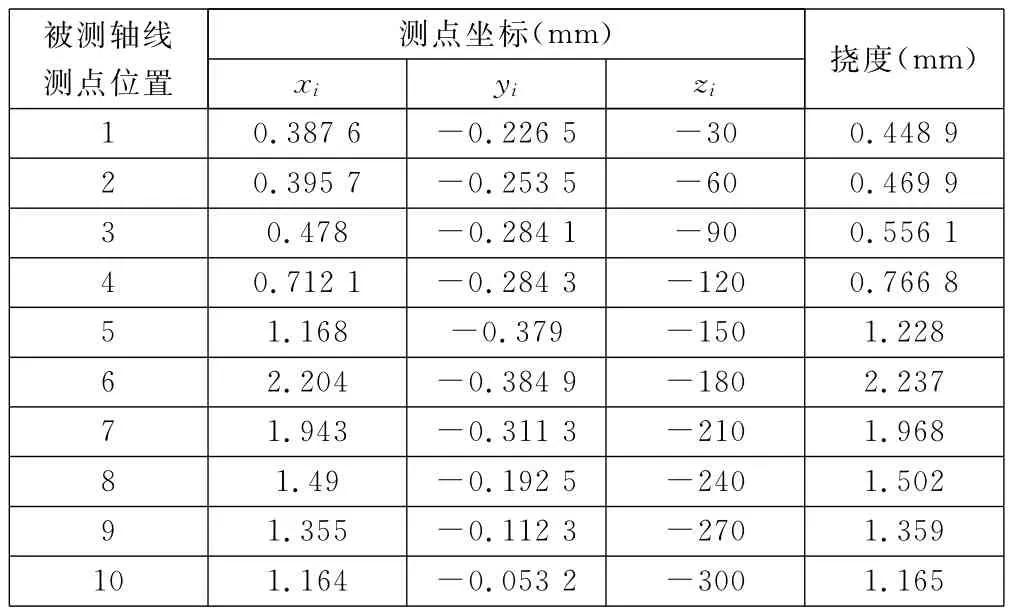
表1 加工前轴线位置坐标及挠度
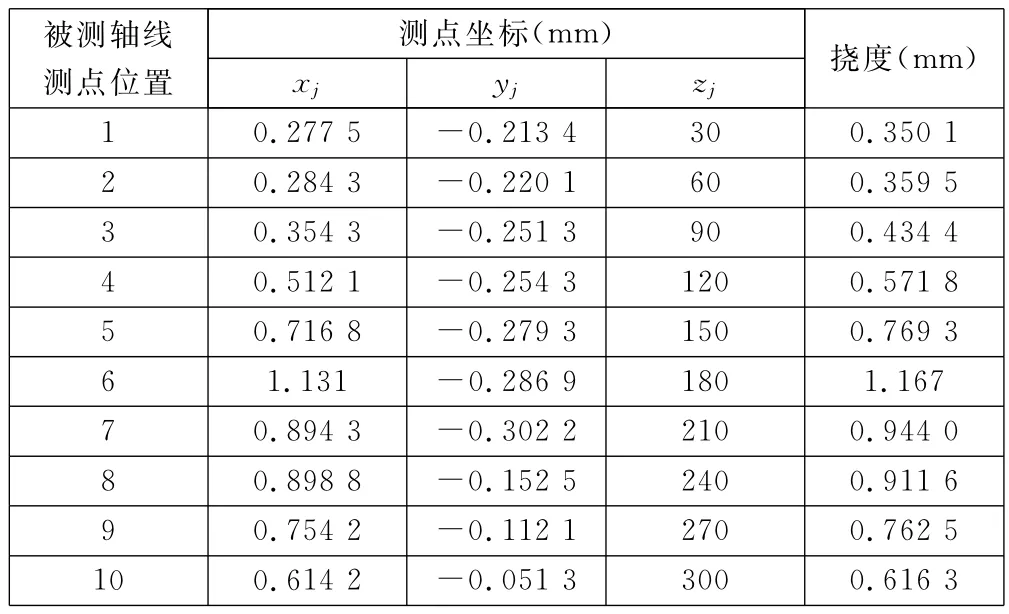
表2 加工后轴线位置坐标及挠度
4 结束语
本文主要介绍了外圆旋风铣床的运动原理与实际加工情况,从几何结构角度建立数学模型分析铣削细长轴类零件直线度误差的变化范围。通过实际加工,观察整理铣削细长轴类零件的被测参数,验证其精度满足要求,可用于实际生产装配。
[1]孙兴伟,崔海,王可,等.变径细长轴类零件的旋风铣削方法研究[J].制造技术与机床,2010(4):107-109.
[2]机械科学研究院和中国计量科学研究院.GB/T 11336-2004,直线度误差检测[S].北京:中国标准出版社,2005:1-2.
[3]邓彬,李庆芬.基于 MATLAB的直线度误差评定的程序设计[J].现代机械,2010(1):62-63.
[4]王敬赓.解析几何[M].北京:高等教育出版社,2010.
[5]胡璇,王为,邓援超.轴类零件轴线测量中基于MATLAB的曲线拟合[J].湖北工业大学学报,2010(10):29-31.

