非线性破坏准则下考虑坡顶条形基础的边坡稳定性分析*
刘 斌,黄 震,刘 雄,刘清裕
非线性破坏准则下考虑坡顶条形基础的边坡稳定性分析*
刘 斌1,黄 震1,刘 雄1,刘清裕2
(1.长沙理工大学交通运输工程学院,湖南长沙410004;2.长沙理工大学文法学院,湖南长沙410004)
运用非线性破坏准则对边坡稳定性进行分析时需考虑的变量比线性情况多.基于非线性Mohr-Coulomb破坏准则,在考虑坡顶条形基础附属荷载情况下对边坡的稳定性进行了分析,采用极限分析原理对边坡的高度表达式进行了推导,并结合序列二次规划算法进行计算.再根据计算方法对工程实例进行计算,将结果与已有研究结果相比较,验证了该计算方法的正确性.
边坡稳定性;非线性准则;条形基础;极限分析
随着我国高速公路建设过程的推进,边坡稳定性问题日益凸显,如果处理措施不当,将造成不可挽回的巨大经济损失.因此,边坡稳定性一直是学术界研究的一个热点问题[1-5].在已有的研究中,大多数边坡稳定性分析是基于线性破坏准则进行研究,Chen[6]在其著作中基于线性破坏准则,采用极限分析方法给出了大多数情况下边坡的稳定性分析结果,其研究成果为边坡稳定性研究提供了重要的指导;陈祖煜[7]对土力学经典问题的上、下限解进行了研究,并给出了计算结果.然而,大量试验数据表明,岩土介质服从非线性破坏准则,已有的线性破坏情况只是非线性破坏准则的一种特殊情况.对于非线性破坏准则而言,其研究成果相对线性破坏成果较少,已有的研究成果也难以应用到工程实际以及理论研究当中.Yang等[8-10]首次基于非线性破坏准则将极限分析方法应用于边坡稳定性分析当中,为处理边坡稳定性工程难题提供了重要参考,使极限分析方法得到了更为广泛的应用.
在土地资源日益紧缺的今天,边坡顶部设置各种建筑物成为一种合理利用土地资源的手段,张晓曦[11]在考虑边坡顶部设置固定荷载的情况下,对边坡的稳定性进行了分析,为山区公路边坡的稳定性及处治提供了参考.本文基于非线性破坏准则,并考虑在边坡顶部设置条形基础荷载情况下,对边坡进行稳定性分析.构建了在条形基础作用下的边坡破坏机构,同时利用非线性破坏准则对边坡的内外做功功率进行推导,计算了条形基础荷载对边坡内外做功功率的影响,令边坡处于极限状态,求解边坡的临近高度,采用非线性规划算法对其结果进行计算,将本文所得结果与已有研究相比较,为实际工程中边坡稳定性设计和施工提供了指导意义.
1 基本原理
在岩土工程研究当中,为了计算的简便,通常采用的强度准则为线性的Mohr-Coulomb准则,在线性准则中,其最大主应力σ1和最小主应力σ3为线性关系:

式(3)当中,σ1和σ3为土体破坏时的最大以及最小主应力,qp、Mp和岩体的土体强度指标c、φ之间的关系为:

但是,大量的实验表明,在土体当中,其最大与最小主应力的关系并非是线性的,大多数研究考虑的两者的线性关系只是一种特殊情况.其非线性关系可以表达如下:

上式当中,M*p和α是由室内三轴试验所确定的参数,此公式是Bieniawski在线性强度破坏准则的基础上提出的.在应力空间(τ,σn)中,上式可以表示如下:
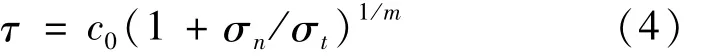
将上述关系式用曲线表示如图1所示,其中c0为纵轴的截距,c0,σt和m均为室内三轴试验所确定土体参数.令m=1,则所研究的非线性破坏准则退化为线性准则.
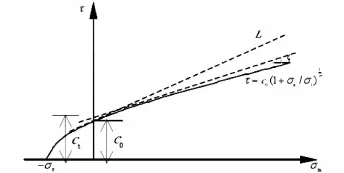
图1 非线性屈服准则的切线
式(4)的切线方程可表示如下:

式(5)中:ct,tanφt为切线的截距和斜率,如上图1中所示,在非线性破坏准则当中,ct,tanφt可表示如下:

2 条形基础荷载作用下边坡的上限分析
构建如图2所示的边坡在条形基础作用下的旋转破坏机构,其中曲线AB为旋转破坏机构的假象破坏面,边坡坡脚为β,边坡顶部BC长度为L,边坡的高度为H,所构造的旋转破坏机构旋转中心O与边坡的B、A连线与水平夹角分别为θ0,θh.由参考文献可知,在本文的破坏机构中,潜在破坏面AB的曲线方程可表示为:
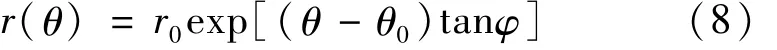
直线OA的长度为:
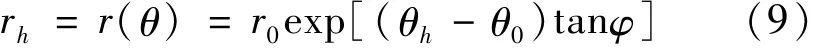
图2所示在条形基础作用下的边坡的破坏机构中,潜在破坏面AB以上的土体可视为假象刚体,并绕破坏机构的旋转中心O做旋转运动,则由图中的几何关系可得:

图2 条形基础荷载作用下边坡的对数螺旋线破坏机构
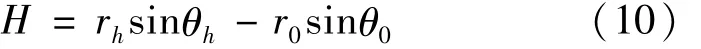
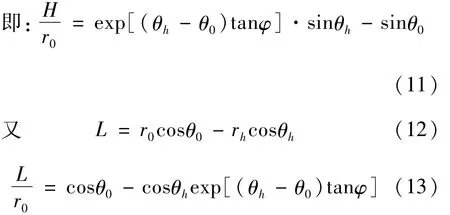
2.1外部做功功率
在Chen的著作当中可知,在分析边坡的旋转破坏机构时,如果对分析的土体自重做功功率时,直接对其进行求解,则过程过于繁琐,并且结果不易求得,只能是一个近似解,因此在本文对图2边坡的外部做功功率求解时,采用的方法为间接的叠加法:首先分别求出OAB、OBC、OAC三个部分的做功功率,进而求得要求的ACB区域的做功功率,其中OAB的做功功率相对OBC、OAC两个三角形的土体做功功率较为难求,本文采用积分的手段进行求解,可得OAB部分做功功率为:
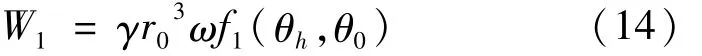
其中:
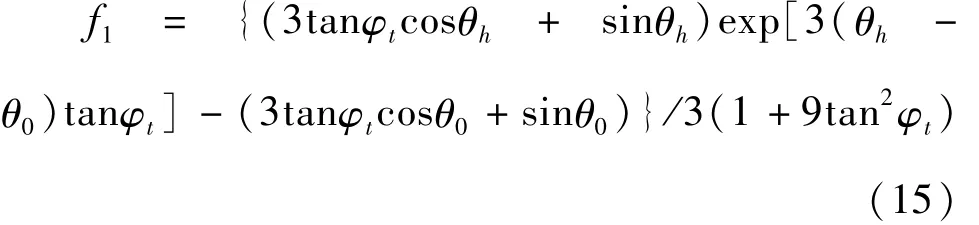
O-B-C的重力做功功率可表示如下:

同理可得OAC土体自重做功功率表达式为:
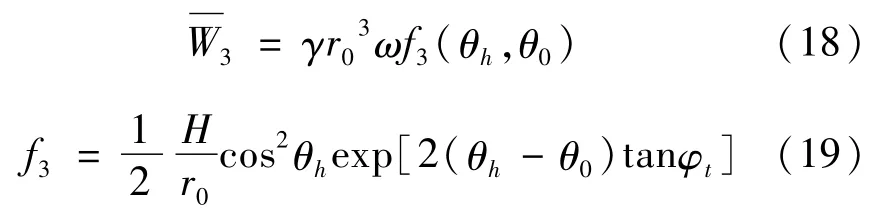
因此由(14)、(16)、(18)式可得,本文所求ACB区域土体外部做功功率为:
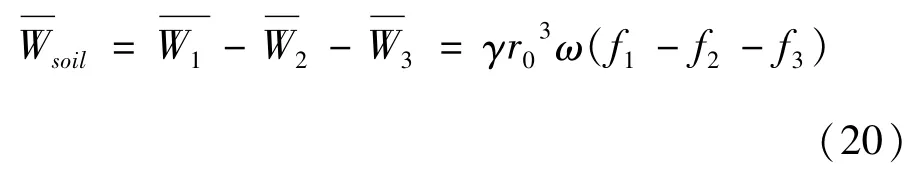
2.2土体内部耗散功率
由极限分析原理可知,旋转刚体的内部能量耗损发生在间断面AB上,沿着间断面AB进行积分即可得旋转刚体的土体内部能量耗散功率:
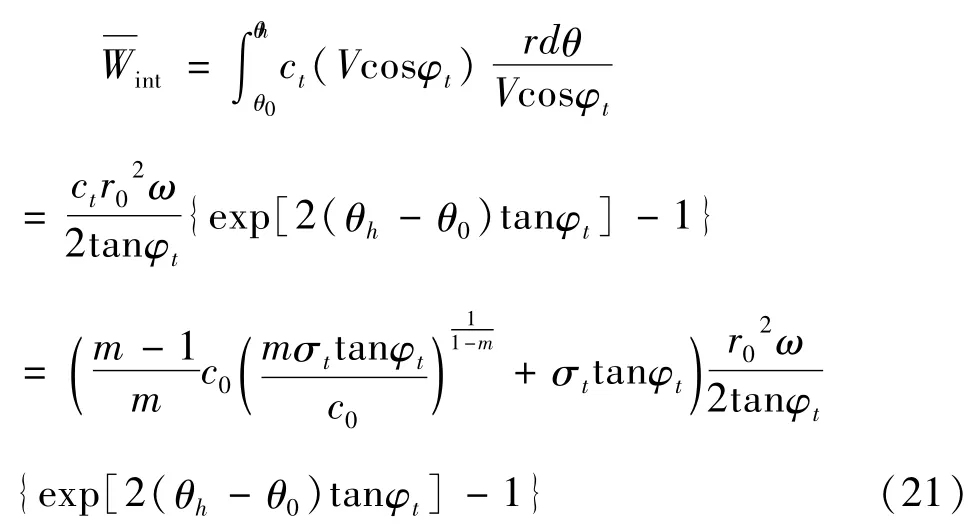
2.3条形基础荷载做功功率
条形基础荷载分布图2所示,条形基础与坡顶C的距离为L0,埋深为d,基础宽度为b,假设其附加均布荷载为q.本文假设回填土的重度、条形基础的重度和二级边坡土体的重度比较接近,其差别对边坡的影响可以忽略不计.故可认为条形基础的附加荷载为上部结构传递到基底的平均值:
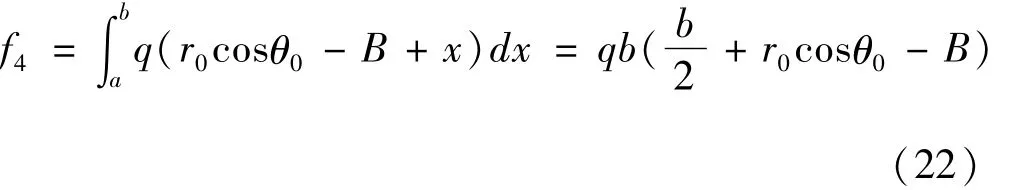
由式(20)及式(22)可得,边坡总的外力做功功率为:
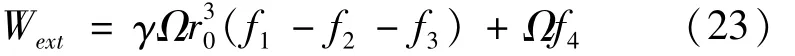
由极限分析上限法定理可知,土体外部做功功率与内部能量耗散功率相等时,图2中旋转刚体达到一个临界状态,可知:

当在条形基础附加荷载作用下边坡的各项功率满足公式(24)时,旋转刚体体达到临界状态,在非线性Mohr-Coulomb破坏准则下,对于在条形基础附加荷载作用下边坡的稳定性分析时,相比线性准则的3个变量就能确定其滑动面方程而言,非线性准则下要采用4个变量,分别为θ0,θh,r0,tanφt,进而确定边坡在平衡状态的临界高度Hcr.
由公式(10)、(12)、(20)、(21)、(23)以及(24)可知,条形基础附加荷载作用下边坡的高度H可以表示为θ0,θh,r0,tanφt的函数.故采用极限分析原理求条形基础附加荷载作用下边坡的临界高度,可转化为数学优化问题:

当在条形基础附加荷载作用下边坡的滑动土体处于临界状态时,H即为最小值,也是式(25)的最小值令,进而对θ0,θh,r0,tanφt进行求解.
其约束条件可确定如下:
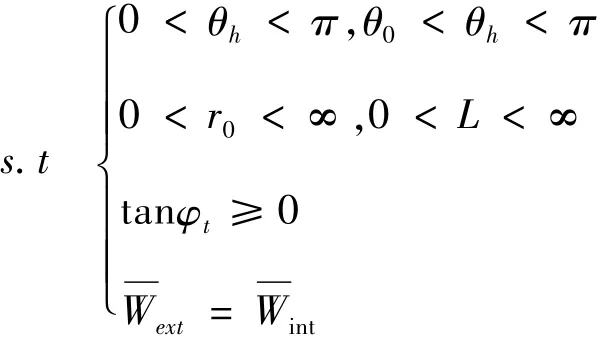
本文采用Chen提出的边坡稳定系数概念,公式(25)给出了临界高度的一个上限解min H.
记

称无量纲系数Ns为边坡稳定系数.
3 工程算例
为了便于比较,假设某边坡坡脚β=90°,即为竖直边坡.采用已有研究将本文中非线性破坏准则下考虑坡顶条形基础附属荷载作用所得边坡的稳定系数与已有的研究结果[12]相比较,设某竖直边坡的土体服从非线性破坏准则,Zhang等[13]在对边坡的稳定性进行分析时,所取的岩土强度参数分别为c=90kPa、σt=247.3kPa,此后也有许多学者基于非线性准则及相同的强度参数分析岩土的稳定性.因此,本文所取的计算参数也同样采用上述参数值.非线性破坏准则中,其非线性系数m决定着破坏准则的强度包络线形状,对岩土的其他参数有着较大影响,故本文对不同非线性系数下的边坡稳定性进行研究.由于本文考虑坡顶条形基础荷载的作用,边坡的稳定性系数将比文献[12]中会小.
当m分别取值为1.0,1.2,1.4,1.6,1.8,2.0,2.5,其他参数与文献[12]中所述相同,并将本文的计算结果与文献[12]中所得结果相比较,结果见表1.从表1中可看出,在非线性Mohr-Coulomb破坏准则下,考虑坡顶条形基础附属荷载,边坡的稳定性系数Ns相比文献[12]中较小,随着m系数的增加,两者相差也越来越大,当m=2.5时,其稳定系数为3.44,与文献[12]中相差达到22.6%.从而可以看出条形基础附加荷载对边坡稳定性的影响,也验证上文提到的本文计算的正确性.

表1 非线性破坏准则下考虑条形基础荷载时边坡稳定性系数与已有结果的比较
4 结论
(1)在非线性破坏准则下,对边坡的稳定性分析时要考虑的变量比线性情况要多一个土体参数.运用极限分析原理对边坡的高度表达式进行了推导,并采用序列二次规划算法进行计算,从而求得条形基础荷载对边坡的稳定性系数的影响.
(2)将本文研究方法应用的工程实例当中,并将所得计算结果与已有研究结果相比较,可以得出,在非线性Mohr-Coulomb破坏准则下,考虑坡顶条形基础附属荷载下,边坡的稳定性系数Ns相比已有结果中较小,随着m系数的增加,两者相差也越来越大.
[1]龚晓南.土塑性力学[M].杭州:浙江大学出版社,1999.
[2]杨小礼,李亮,刘宝琛.非线性破坏准则对竖直边坡稳定性分析的影响[J].岩石力学与工程学报,2004,(4):592-596.
[3]李家春.公路边坡降雨灾害评价方法与指标研究[D].西安:长安大学博士学位论文,2005.
[4]钟闻华,刘松玉,张克恭.群桩基础特性研究与实例分析[J].建筑结构,2003,(11):9-12.
[5]夏元友,李梅.边坡稳定性评价方法研究及发展趋势[J].岩石力学与工程学报,2002,(7):1087-1091.
[6]Chen W.Limit Analysis and Soil Plasticity[M].Amsterdam:Elsevier,1975.
[7]陈祖煜.土力学经典问题的极限分析上下限解[J].岩土工程学报,2002,(1):1-11.
[8]Yang X,Yin J.Slope stability analysiswith non-linear failure criterion[J].Journal of Engineering Mechanics,2004,(3):267-273.
[9]Yang X.Seismic displacementof rock slopeswith nonlinear Hoek-Brown failure criterion[J].Rock Mechanics&Mining Sciences, 2007,(6):948-953.
[10]杨小礼.岩石极限分析非线性理论及其应用[J].中南大学学报,2009,(11):225-229.
[11]张晓曦.边坡工程稳定性极限分析[D].成都:西南交通大学硕士学位论文,2011.
[12]胡卫东,张国祥.非线性破坏准则下的边坡稳定塑性极限分析[J].岩土力学,2007,(9):1909-1913.
[13]Zhang X,ChenW.Stability analysis of slopeswith general nonlinear failure criterion[J].International Journal for Numerical and Analytical Methods in Geomechanics,1987,(1):33-50.
Slope Stability Analysis under the Nonlinear Failure Criterion w ith the Consideration of the Crest Strip Foundation
LIU Bin1,HUANG Zhen1,LIU Xiong1,LIU Qingyu2
(1.College of Transportation Engineering,Changsha University of Science and Technology,Changsha Hunan 410004,China;2.College of Arts and Law,Changsha University of Science and Technology,Changsha Hunan 410004,China)
It is necessary to considermore variables to analyze slope stability by using nonlinear failure criterion compared to the linear case.Based on nonlinearMohr-Coulomb failure criterion,affiliated load of the creststrip foundation is considered to analyze the slope stability.Slope height expressions are deduced by the principle of limitanalysis,and they are calculated with sequential quadratic programming algorithm.Then the paper calculates the engineering practicewith the calculationmethod,and the results are compared with those of previous studies to verify the correctness of the calculationmethod.
slope stability;nonlinear criteria;strip foundation;limit analysis
TU47
A
1008-4681(2014)02-0015-05
(责任编校:晴川)
2013-12-31
刘斌(1990-),男,江西吉安人,长沙理工大学交通运输工程学院硕士生.研究方向:特殊土路基、边坡稳定性.
——结构相互作用的影响分析

