一种基于评价函数的三维矩形布局遗传算法
甄士刚,王金敏
(天津职业技术师范大学机械工程学院,天津 300222)
布局问题广泛存在于生产生活实际中,例如货物的运输、机械零部件的分布、车间厂房的布置等,对布局问题的有效解决,具有极大的现实意义。长期以来,人们主要通过启发式算法[1]解决布局问题。例如张德富等[2]将构造启发式算法与模拟退火算法结合,提出一种求解三维布局问题的混合模拟退火算法;Bortfeldt等[3]将多线程搜索应用于禁忌搜索算法,提出一种并行禁忌搜索算法;Gehring等[4]提出了解决三维布局问题的并行遗传算法;Parreno等[5]基于最大空间概念的构造堆算法,进一步发展和改进了一种贪心随机自适应搜索算法;He等[6]基于古语“金角银边草肚皮”提出一种针对三维矩形布局问题的高效定位启发式算法。本文针对三维矩形布局问题,通过将构造启发式算法的定位和定序结合,提出一种基于评价函数的布局遗传算法。
1 三维矩形布局问题
三维矩形布局问题的数学模型描述如下:
设布局空间的体积为V,布局空间的体积利用率为f,则目标函数

式中:lk、wk、hk分别为第k个已布入矩形块的长、宽、高;n为布入的矩形块块数。布局结果由体积利用率f来衡量,f值越大布局结果越好。约束条件

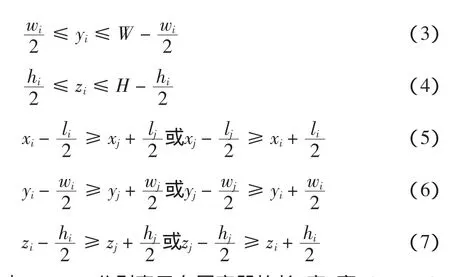
式中:L、W、H分别表示布局容器的长、宽、高;(xi,yi,zi)和(xj,yj,zj)分别为第i个和第j个已布入物体的中心点坐标,且i≠j,i、j∈k。这里布局容器的左下前角为坐标原点(0,0,0)。li、wi、hi和lj、wj、hj分别为第i个和第j个已布入矩形块的长、宽、高。式(2)(3)(4)保证物体完全布入到布局空间中,式(5)(6)(7)保证两布入物体之间不发生干涉。
另外,本文算法中矩形空间以及矩形块的长>宽>高,矩形块的长宽高尺寸不做交换,即矩形块满足方向约束,在布局过程中不可以旋转。
2 基于评价函数的构造启发式算法
构造启发式算法通过一个一个地增加解的构造元素来求得可行解,它的循环次数与问题解的构造元素个数成正比,而与解空间的大小无关,因此,计算速度很快。
布局问题中的构造启发式算法主要由定序规则和定位规则所决定,不同的定序规则和定位规则可以产生不同的构造布局算法。定序规则确定每一个矩形块放入布局空间中的先后顺序;定位规则确定每一个矩形块在布局空间中的摆放位置。定序和定位规则一旦确定,布局过程也就确定。本文所采用的定序规则和定位规则介绍如下。
2.1 定序规则
通常,人们通过比较矩形块的某一项或某几项属性(如体积、面积等)来建立定序规则。本文提出一种基于评价函数的定序规则。评价函数为:

式中:vi、li、wi、hi分别为第i个布局块的体积、长、宽、高;v、l、w、h分别为布局空间的体积、长、宽、高;α、β、χ、δ均为参数,且α+β+χ+δ=1。
本文算法先确定α、β、χ、δ这4个参数值,然后根据已知矩形块和布局空间的长宽高计算出每个矩形块对应的函数值。当所有矩形块计算完之后,依据从大到小的顺序对函数值进行排序。函数值的排列顺序也就是相应矩形块的布局顺序。例如最大函数值对应标号为5的矩形块,那么标号为5的矩形块将首先布局。
该定序规则包含了一般情况下人们所使用的定序规则。在式(8)所示评价函数中取α=1,其余参数得0。这时按照评价函数函数值递减布局,也就是按照体积递减布局。在式(8)中,当取β=1,其余参数得0。结果恰好是按照最长边递减布局。
若是2个或2个以上矩形块评价函数函数值相等,则先计算函数值的矩形块先于其他矩形块布入。
2.2 定位规则
本文采用吸引子定位评价函数对矩形块进行定位。吸引子法可参见文献[7]。
定位评价函数的具体形式为:
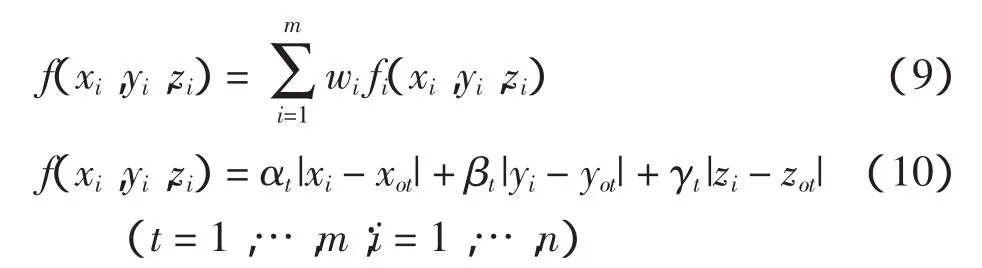
式中:f(xi,yi,zi)为总的定位评价函数;fi(xi,yi,zi)为关于各个吸引子的定位评价函数;m为吸引子的个数,这里m=4;t=1、2、3、4表示吸引子分别位于布局空间4个角点,如图1中4个黑点所示;xot、yot、zot代表吸引子在布局空间中的3个坐标;ωt为各个吸引子定位函数之间的权重为每个吸引子定位函数内部权重,αt+ βt+ γt=1。
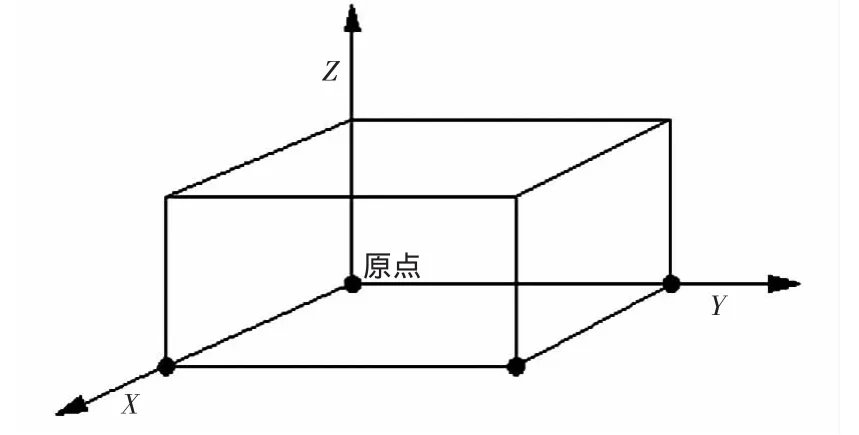
图1 吸引子位置
类似定序规则的建立,定位规则首先确定定位评价函数的12个参数。然后通过比较备选布局点的函数值,将函数值最小的备选点作为矩形块的布局位置。
3 布局遗传算法
基于评价函数的构造启发式算法共有15个可供选择的参数。参数值不同,布局过程不同,布局结果也不同。要想使布局空间利用率最大,需要找到与之对应的15个参数的参数值。显然,三维矩形布局问题的求解可化为一个15维的函数优化问题。本文采用遗传算法[8]来优化参数。基于评价函数的构造启发式算法加上遗传算法优化构成布局遗传算法。
3.1 遗传算法
3.1.1 编码策略
采用实数编码的方式,每个染色体是变量为20维的解向量。编码向量表示为:S=(B1,B2,…,B20)。各个分向量分别对应算法的20个参数。
3.1.2 适应度函数及初始化
算法的适应度函数取布局空间的体积利用率f。适应度值越大,布局空间的利用率就越大,个体的性能也就越好。
本文在产生初始种群时,采用如下方式进行:
首先由计算机随机产生,然后再做归一化处理得到具体参数值。例如,随机之后B1=0.7,B2=0.6,B3=0.4,B4=0.3;为保证参数之和等于1,分别用各个参数除以4个参数之和,结果对应定序评价函数α=0.7/(0.7+0.6+0.4+0.3)=0.35,同理 β=0.3,χ=0.2,δ=0.15。
3.1.3 选择算子
在选择配对个体时采用蜜蜂进化选择法[9],其主要步骤:
①选取第N代种群中的最优个体与上一代蜂王(适应度最好值)比较,优胜者作为第N代蜂王,记为Queen。
②通过选择算子从第N代种群中选出(n/2)λ(0≤λ≤1)个个体,随后随机产生(n/2)(1- λ)个个体。
③上述(n/2)个个体和第N代蜂王作为配对交叉的父本。
3.1.4 交叉算子
令选择算子中的Queen分别与上述(n/2)个个体交叉配对。具体交叉策略为:
(1)单点交叉。随机生成一个交叉位点,将两父代中交叉位点之前的基因进行整体交换,被交换基因之间的相对顺序不变,从而生成2个新的子代个体;
(2)双点交叉。随机生成2个交叉位点,将两父代交叉位点之间的基因进行整体交换,被交换基因之间的相对顺序不变,从而生成2个新的子代个体。
3.1.5 变异算子
对当前种群中的个体进行变异操作,是产生新解和维持种群多样性的有效手段。本算法采用均匀变异:设新的个体中的分向量为Xk;k∈N且k∈[1,20],随机产生一个变异位,用新产生的[0,1]之间的数代替这个基因。
3.2 布局遗传算法流程
算法首先设定进化代数N、交叉概率PXOVER、变异概率PMUTATION以及蜜蜂进化选择算子比例系数λ,然后随机产生初始种群,计算个体适应度。算法以最大进化代数作为停止条件,若满足停止条件,则停止计算;否则,对个体进行选择、交叉、变异操作。当满足终止条件时,输出优化参数值和布局方案。
具体步骤如下:
①设定最大进化代数、交叉变异概率以及蜜蜂进化选择算子系数,随机生成初始种群。
②基于初始种群确定的20个参数的参数值,计算出各个矩形块的评价函数值,得出相应的定序和定位规则,实现布局过程。
③计算种群中所有个体的适应度,将最优个体(即第N=0代蜂王)保存到best中。
④N=N+1。
⑤如果满足停止条件,算法输出结果并停止运行;否则,继续。
⑥利用蜜蜂进化选择算子,从A(N-1)中选出父代个体。
⑦父代个体进行交叉操作产生种群B(N)。
⑧对B(N)执行变异操作,得到种群C(N)。
⑨基于种群C(N)确定的20个参数的参数值,计算出各个矩形块的评价函数值,得出相应的定序和定位规则,实现布局过程。
⑩计算种群C(N)中所有个体的适应度,将适应度最大的个体记为newbest。
⑪如果newbest的适应度值大于best的适应值,用newbest代替best;否则,用newbest代替C(N)中最差的个体;得到第N代种群。
⑫转到④。
4 算例分析
本文的基于评价函数的布局遗传算法采用C++实现,计算环境为:Pentium D C-PU,2 GB内存,2.79 GHz PC机。在以下计算中,算法进化代数、交叉概率、变异概率以及蜜蜂选择算子的比例系数分别取N=20,PXOVER=0.85,PMUTATION=0.15,λ =0.8。具体计算中,每组数据计算10次,选取最好的计算结果作为最终结果。
本文采用文献[10]的后6组数据。每组有100个算例。所有矩形块的尺寸均为整数,矩形块的长宽高尺寸区间分别为[30,120]、[25,100]和[20,80]。具体的算例计算和比较结果见表1。

表1 各算法计算结果的利用率%
表1中利用率为平均利用率,是将100个算例最终结果相加取平均得到。对于这些算例,很多学者都进行了研究测试。Bischoff等[10]提出启发式算法H_BR;Gehring等[11]提出GA_GB算法;Bortfeld等[12-13]提出禁忌搜索法TS_BG和混合遗传算法HGA_BG以及并行遗传算法PGA_GB[4];Moura等[14]提出GRASP算法。
从表1可以看出,BR14、BR15高出了其他所有算法结果,BR15高出对应最大值1.33%,BR14高出对应最大值0.94%。算例BR10—BR13结果虽然没能高出其它所有算法,但是均高于上述其余6个算法结果中的4~5个,整体来看算法效果良好。
5 结束语
本文针对三维矩形布局问题,通过提出基于评价函数的定序和定位规则,创造性地将决定定序和定位规则的参数编码于同一个基因向量中,从而将布局问题转化为参数优化问题。经过算例测试和分析,本文算法取得了良好的计算结果。另外,算法也存在一些需要解决的问题,例如,如何通过初始化参数的方法进一步优化布局结果,如何通过将本文基于评价函数的定序规则与分割空间策略结合来进一步优化布局结果,这将是今后的工作内容。
[1]SWEENEY P E,PATEMOSTER E R.Cutting and packing problems:A categorized,application-oriented research bibliography[J].TheJournalofOperational Research Socitey,1992,43(7):691-706.
[2]张德富,彭煜,朱文兴,等.求解三维装箱问题的混合模拟退火算法[J].计算机学报,2009,32(11):2147-2156.
[3]BORTFELD T A,GEHRING H,MACK D.A parallel tabu search algorithm for solving the container loading problem[J].Parallel Computing,2003,29(5):641-662.
[4]GEHRING H,BORTFELD T A.A parallel genetic algorithm for solving the container loading problem [J].International Trasactions in Operational Research,2002,9(4):497-511.
[5]PARRENO F,ALVAREZ-VALDES R,OLIVEIRA J F,et al.A maximal-space algorithm for the container loading problem[J].INFORMS Journal on Computing,2007,20(3):412-422.
[6]HE K,HUANG W.An efficient placement heuristic for threedimensional rectangular packing[J].Computers&Operations Research,2011,38(1):227-233.
[7]王金敏,杨维嘉.动态吸引子在布局求解中的应用[J].计算机辅助设计与图形学学报,2005,17(8):1725-1729.
[8]王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
[9]孟伟,韩学东,洪炳熔.蜜蜂进化型遗传算法[J].电子学报,2006,7(34):1294-1300.
[10]BISCHOFF E E,RATCLIFFB S W.Issues in the development of approaches to container loading[J].Omega,1995,23(3):377-390.
[11]GEHRING H,BORTFELDTA.A genetic algorithm for solving the container loading problem[J].International Transactions in Operational Research,1997,4(6):401-418.
[12]BORTFELD T A,GEHRING H.A tabu search algorithm for weakly heterogeneous container loading problems[J].OR Spectrum,1998,20(4):237-250.
[13]BORTFELD T A,GEHRING H.A hybrid genetic algorithm for the container loading problem[J].European Journal of Operational Research,2001,131(1):143-161.
[14]MOURA A,OLIVEIRA J F.A GRASP approach to the container loading problem[J].IEEE Intelligent Systems,2005,20(4):50-57.

