基于多核的MCMC图像去噪算法并行实现

成敏，张建州，于岩

1.四川大学计算机学院，成都 610065

2.中国人民解放军78098部队

基于多核的MCMC图像去噪算法并行实现

成敏1，2，张建州1，于岩1

1.四川大学计算机学院，成都 610065

2.中国人民解放军78098部队

图像在获取、传输和存贮的过程中，总是不可避免地受到各种噪声源的干扰。为抑制图像噪声，改善图像质量，从图像中获取更准确的信息，需要对图像进行去噪处理。图像去噪是图像分割、复原等后续处理的重要前提条件[1]，是图像处理领域中十分关键的技术，也一直是图像处理领域的难题。

针对高斯噪声，常见的去噪方法有：高斯滤波、小波变换域滤波、非局部均值滤波[2-3]、偏微分方程滤波等。随着马尔可夫链蒙特卡洛方法在统计学应用领域的发展，马尔可夫链蒙特卡洛方法也运用到了图像去噪中。

马尔可夫链蒙特卡洛去噪算法[4]是通过随机抽取变化的图像，根据样本的条件概率分布，制定一个贝叶斯最小二乘法[5-6]，在S.Geman和D.Geman[7]对图像的贝叶斯重建研究中，最大限度地得到原始图像条件概率，然后运用后验估计的迭代模拟方法解决图像去噪，这是一种非参数的随机方法。马尔可夫链蒙特卡洛的去噪方法，以灵活的方式适应了原始图像的噪声统计。

高斯噪声图像运用MCMC方法去噪后，图像有明显斑点，高噪声情况下去噪效果不理想。Chatterjee和Milanfar[8-9]在高斯噪声环境下的实验说明，对图像进行预去噪处理可以降低噪声产生的影响，有利于进行分类和聚类。因此，本文在用MCMC方法进行去噪前先对噪声图像进行简单的均值滤波预处理，既去除了图像中部分噪声，也有利于随机聚类，减少斑点。

在MCMC方法中，需要知道噪声方差，但在实际应用中，噪声方差显然是不可知的，所以需要对噪声方差进行估计。本文运用成熟的Donoho和Johnstone[10]频域采样法进行噪声方差估计。

由于在MCMC方法中，每个像素点的计算都是独立的，本文利用多核硬件计算资源，将算法进行并行处理[11]，提高了计算速度。在图像规模较大的情况下，加速比更加明显。

1 马尔可夫链蒙特卡洛方法

1.1 问题模型

设S是图像，s是图像上的一个像素，s∈S。被噪声污染的原始图像是F={F(s)|s∈S}，无噪声的图像是G={G(s)|s∈S}，s上的随机噪声为N={N(s)|s∈S}。F，G和N之间的关系通常可以表示为[12]：

求的是G(s)，从公式（1）可看出，这其实是一个逆问题，最终只能求得G(s)的估计值，因此这被视为解决后验估计的问题。运用贝叶斯最小二乘法来解决这个估计问题。

从公式（3）可以知道，G(s)的最佳估计值是E(G(s)|F(s))，G(s)是F(s)条件下的均值。但需要用一个非常复杂的非线性函数F(s)来计算。若要解决这个问题，计算式可作一个简单的贝叶斯线性最小二乘式，建模后p(G(s)|F(s))使用参数统计模型。但使用这种方法往往导致噪声强度大的图像去噪更加复杂。

为使G(s)的估计值更接近于真实值，分析后，决定使用重要性加权马尔可夫链蒙特卡洛后验估计方法。这种方法在一个全图的范围内考虑该像素的灰度值，将非参数近似计算p(G(s)|F(s))记为(G(s)|F(s))。在这种方法中本地空间强度的相互作用重在允许改善无噪声图像G(s)，噪声N(s)的地方空间强度的相互作用在这里就会表现得非常弱。

1.2 马尔可夫链蒙特卡洛去噪算法

初始化：Ω是一个估计出来的目标分配序列样本集，Ω={s0，s1，…，sη}。初始序列样本Ω，令s0=s。

第1步第k次迭代的候选样本从公式（4）的Q(s′k|sk-1)分布中随机抽取。

其中σs表示分布函数Q(s′|sk-1)的方差。

第2步由公式（5）计算接受概率α(s′k|sk-1)。

第3步由均匀分布U(0，1)生成一个随机值u。

第4步如果u≤α(s′k|sk-1)，将候选样本s′k纳入样本序列Ω中，否则，舍弃s′k。

第5步重复1～4步，迭代m次。

第6步将样本序列Ω中的样本权值，建立一个权值集[13]。

第7步将公式（7）中的权值代入公式（8）中，估计后验概率密度函数(G(s)|F(s))。

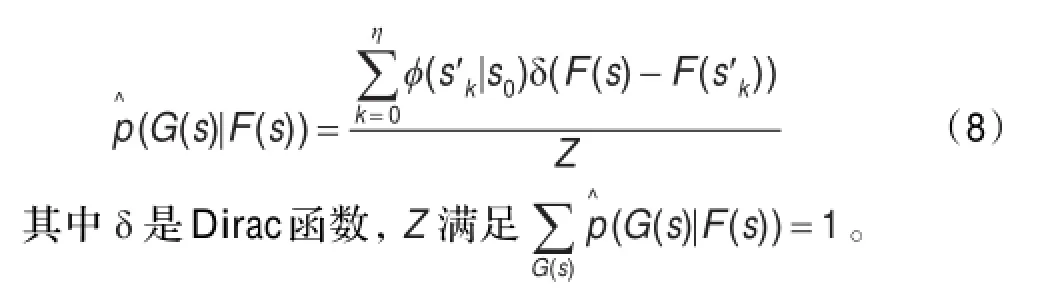
1.3 噪声图像均值滤波预处理

均值滤波是一种平滑线性空间滤波，将包含在滤波掩模确定邻域内像素作简单平均，用平均灰度值去代替图像每个像素点的值。图像灰度尖锐变化是图像边缘的特性，本文采用均值滤波作预处理后，图像边缘特性削弱，所以处理后存在着不希望的边缘模糊的负面效应。

1.4 噪声方差估计

公式（6）需要知道噪声方差，但在实际应用中，处理含有噪声的图像时，噪声方差是未知的，但噪声方差又是算法中的重要参数，那就只有从噪声图像中估计得出。

噪声方差的估计方法有很多，如K.Rank基于空域的噪声标准差估计，M.Jansen基于小波域的噪声方差估计方法，鲁棒中值绝对估计方法等。本文选用Donoho和Johnstone的频域采样法，这种方法是最简便的。

Donoho噪声估计方法是建立在理想的高斯噪声模型基础上，将图像小波分解的第一级斜向高频子图像作为纯子噪声图来估计原噪声标准方差。公式是MAD/0.674 5，其中MAD是HH带小波系数幅度的绝对值的中值，理想高斯噪声的绝对值中值和标准差的比约是0.674 5。这种采样方法适合高频段含很少图像信息的场合，得到的子图像点数较多，保证了子噪声对原噪声特征的继承。

2 马尔可夫链蒙特卡洛算法的并行实现

2.1 并行计算

图像处理通常存在着时间复杂度和结果图像质量相互矛盾的问题，为了提高图像的处理效果，通常需要花费更多的时间。当串行执行的性能接近最大时，只有通过并行计算等方式提高算法的运算速度。在单机环境下，用多核计算机实现并行计算。在分布式环境下，通常由多处理器和多核计算机来构成分布式的环境。

马尔可夫链蒙特卡洛方法需要计算多次循环迭代，并且循环不依赖于其他迭代的结果，特别适用于并行计算，所以本文将循环迭代进行分组并行计算。因为循环内有通信消耗，所以只有进行大量的复杂计算时才会大大降低时间复杂度。

2.2 并行算法实现

分析本文算法耗时原因发现，计算每个像素点的去噪过程是相同的，将这个图像的大矩阵计算过程进行任务分配，可以在Matlab软件环境下实现并行性[14]。

马尔可夫链蒙特卡洛算法的并行过程如图1所示。

由图1可以看出，循环体的每次执行都是一次迭代，Matlab可以以非特定顺序相互独立地计算每个迭代。因为每个像素点的计算都是独立的，所以没必要保证这些计算的同步性。如果CPU的数量与迭代次数相等，那么每个CPU执行一次迭代。如果CPU数量少于迭代次数，那么有些CPU将执行多次迭代；在这种情况下，为了减少通信的时间，一个CPU可能一次接到多次迭代。

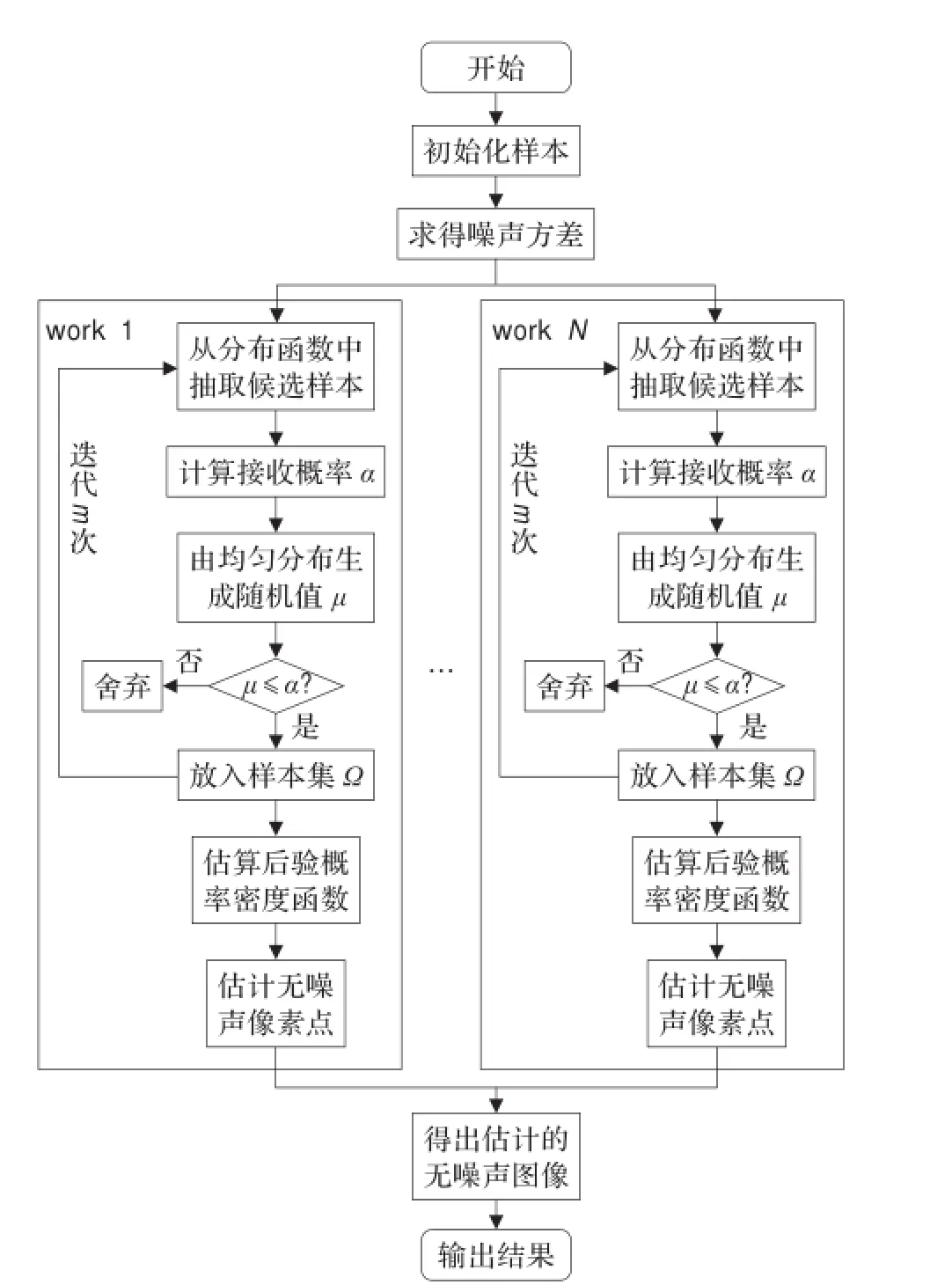
图1 并行计算流程

3 实验

3.1 实验环境及相关参数

实验环境为：Intel®CoreTMi5 CPU M430@2.27 GHz内存2 GB，Win7旗舰版，Matlab R2010（b）。参数的选取为，均值预处理窗口为3×3，空间方差σs=21，迭代次数m=200，搜索窗口为7×7。本文只对该算法的并行计算有效性和可行性进行测试，所以，只采用简单的单机多核进行实验。在以后的实验中将会由多处理器和多核计算机来构成分布式环境。

在Matlab中，首先要用matlabpool[15]启动并行运行环境，设置计算机CPU数量，为了最大地达到计算机的运行速度，一般按照计算机CPU的核数进行设置，在实验中设置为双核。双核运算功能启动后，Windows任务管理器里有三个Matlab.exe进程，其中一个占有内存较多，另两个占有内存一样多。在设计MCMC图像去噪并行处理时，需要使用parfor语句，要注意将不变参数设置在循环体外，生成的随机数等要设置在循环体内，否则运算出来的结果会发生错误。

3.2 本文算法与传统去噪算法效果对比

首先，验证本文去噪方法的有效性，分别选取大小为512×512的“Lena”图像、512×512的“Peppers”图像添加噪声进行实验，并对高斯平滑滤波、维纳滤波[16]进行去噪效果的比较，实验具有很强代表性，实验结果如图2，图3所示。

图2 σn=50图像去噪

图3 σn=50图像去噪

从图2、图3可以看出，常用的一些图像去噪算法在一定程度上削弱了图像噪声，提高了图像的质量，但用高斯平滑去噪方法去噪后，图像变得模糊，边缘特征不清晰；用维纳去噪后图像上仍存在许多明显噪点。本文算法去噪后的图像，噪点基本被去除，边缘特征较清晰。

从图中看出，用MCMC方法可以获得比较好的去噪效果，下面定量分析图像去噪效果。用几种去噪算法对Lena图像和Peppers图像的不同噪声方差图像去噪后所得图像峰值信噪比如表1所示。从表1看出，当噪声水平很小时，维纳去噪方法的效果最好，本文算法略低于该方法，但随着噪声方差的增加，维纳去噪方法的去噪效果越来越不理想，本文提出的算法去噪效果是最好的。

3.3 算法运行时间比较分析

从表2看出，矩阵规模较大（512×512）比计算规模较小（256×256）多核加速明显，这是因为将任务分配给CPU时耗时造成，在计算规模很小的情况下并行得来的性能提升有限，不能弥补这种消耗。

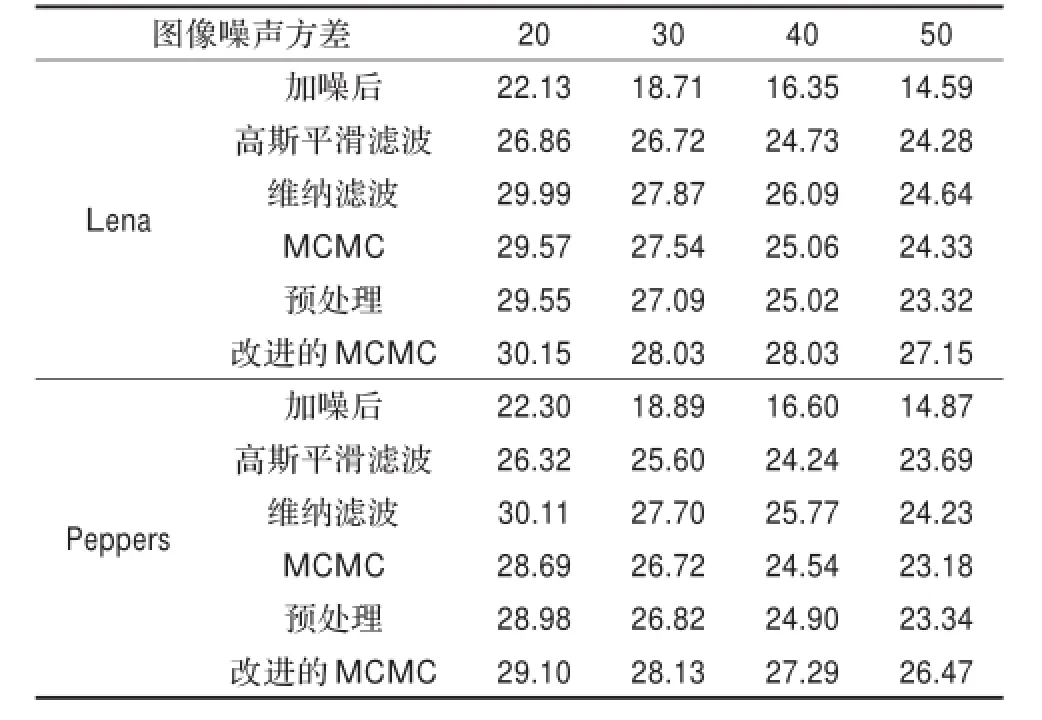
表1 PSNR比较表dB

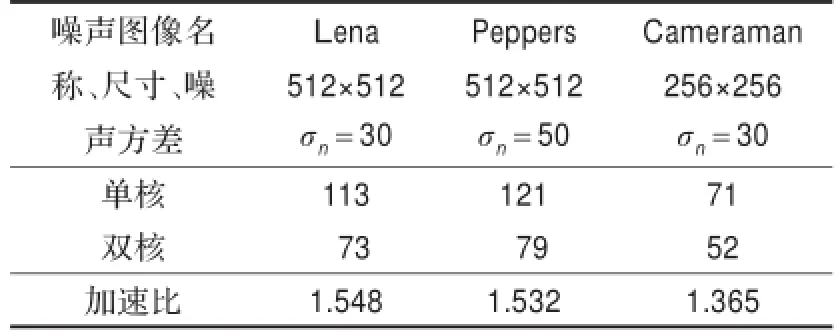
表2 单核和双核运行效率对比s

4 结论与展望

本文用MCMC的并行方法对图像去噪，既保证了去噪效果也提高了运行速度。在这项研究中，通过对噪声图像的预处理，估计噪声方差，使用马尔可夫链蒙特卡洛抽样方法进行随机优化，达到图像去噪的目的。实验是采用添加噪声然后进行去噪来测试该算法信噪比，用数据说明了其去噪性能的优越性。该算法还可扩展为多通道图像，视频和3D数据量。

为了提高MCMC算法的运行速度，特别是该算法运用到视频和3D上时为了解决其计算量的庞大，本文针对MCMC算法的可并行性进行了研究与实现，提高了大规模矩阵的运算速度和多核CPU资源的利用率。本文的并行设计方法为其他类似的数据处理提供了一种将串行任务进行分割的新途径。Matlab丰富的库函数和操作系统上的集群环境、多核的硬件条件可更简捷有效地解决串行程序性能提升方面的瓶颈问题。目前，Matlab并行计算应用发展迅速，将图像放在分布式的环境下将大大提升运行速度。

[1]Gonzalez C.Digital image processing[M].2nd ed.Beijing：Publishing House of Electronics Industry，2011.

[2]Buades A，Coll B，Morel J M.A review of image denoising algorithms，with a new one[J].Multiscale Model Simul，2005，4（2）：490-530.

[3]Buades A，Coll B，Morel J M.On image denoising methods[J].SIAM Review，2010，52（1）：113-147.

[4]Wong A，Mishra A.Stochastic image denoising based on Markov-chain Monte Carlo sampling[J].Signal Processing 2011，91：2112-2120.

[5]Koutrounbss K.Pattern recognition[M].Beijing：Publishing House of Electronics Industry，2009.

[6]Pryce J，Bruce A.Statistical mechanics of image restoration[J].Journal of Physics A：Mathematical and General，1995，28（3）：511-532.

[7]Geman S，Geman D.Stochastic relaxation，Gibbs distributions，and the Bayesian restoration of images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6：721-741.

[8]Chatterjee P，Milanfar P.Is denoising dead?[J].IEEE Transactions on Image Pocessing，2010，19（4）：895-911.

[9]Chatterjee P，Milanfar P.Practical bounds on image denoising：from estimation to information[J].IEEE Transactions on Image Pocessing，2011，20（5）：1221-1233.

[10]Donoho D L，Johnstone I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika，1994，81：425-455.

[11]Downton A，Crookes D.Parallel architectures for image processing[J].Electronics&Communication Engineering Journal，1998，10（3）.

[12]Chan TonyF，Shen Jianhon.Image processing and analysis[M].Beijing：Publishing House of Science，2009.

[13]Chen M.Importance-weighted marginal Bayesian posterior density estimation[J].Journal of the American Statistical Association，1994，89（427）：818-824.

[14]MathWorks.Matlab distributed computing server[EB/OL].（2009-10-01）.http：//www.mathworks.com/help/toolbox/ mdce/index.html.

[15]Gonzalez C.Digital image processing using MATLAB[M]. Beijing：Publishing House of Electronics Industry，2009.

[16]Nowak R D.Wavelet-based rician noise removal for magnetic resonance imaging[J].IEEE Transactions on Image Pocessing，1999，8（10）：1408-1419.

CHENG Min1，2,ZHANG Jianzhou1,YU Yan1

1.College of Computer,Sichuan University,Chengdu 610065,China
2.Unit 78098 of PLA,China

Image denoising is a prerequisite for the many processing tasks of image.Markov Chain Monte Carlo algorithm is an important method of image denoising.However,the method has some problems such that the denoised image has obvious spots,the denoising image corrupted by heavy noise is not satisfactory,the noise variance needs to be estimated in practical application,and the operation speed of this method is slow.This paper proposes a two-step denoising method. It preprocesses the noise image using the mean filter.It estimates the pretreated image noise variance.It uses the MCMC image denoising method.To take full advantage of multi-core processor resources,this paper studies the parallel programming of MCMC algorithm.The multi-core program increases the speed of MCMC algorithm.The experiments show that the denoising method given in this paper reduces spots and improves the signal-to-noise ratio.Parallel processing can make the algorithm more efficient.

image denoising;Markov Chain Monte Carlo（MCMC）;variance estimation;pretreatment;parallel processing

图像去噪是许多图像处理任务的前提。马尔可夫链蒙特卡洛图像去噪算法是很重要的一种图像去噪方法，但去噪后图像存在明显斑点，在高噪声情况下去噪效果不理想，实际应用中需要进行噪声方差估计，运算速度慢。提出两步去噪方法，用均值滤波对噪声图像进行预处理，估计预处理后图像噪声方差，进行MCMC图像去噪；为充分利用多核处理器的硬件资源，研究了将MCMC算法进行并行编程，提高了程序的运行速度。实验表明两步去噪方法减少了斑点、提高了信噪比；并行实现提高了运算效率。

图像去噪；马尔可夫链蒙特卡洛方法（MCMC）；方差估计；预处理；并行处理

A

TP391.9

10.3778/j.issn.1002-8331.1211-0155

CHENG Min,ZHANG Jianzhou,YU Yan.Parallel image denoising algorithm based on multi-core MCMC.Computer Engineering and Applications,2014,50（18）：152-155.

成敏（1976—），女，工程师，主要研究领域为计算机视觉。E-mail：scsdcm@sohu.com

2012-11-14

2013-01-10

1002-8331（2014）18-0152-04

CNKI网络优先出版：2013-01-29，http://www.cnki.net/kcms/detail/11.2127.TP.20130129.1539.011.html