改进粒子群算法的无线传感器网络节点定位

王亚子，杨建辉

周口师范学院数学与统计学院，河南周口 466001

改进粒子群算法的无线传感器网络节点定位

王亚子，杨建辉

周口师范学院数学与统计学院，河南周口 466001

1 引言

无线传感器由许多微型、能量有限的节点组成，节点具有计算、通信和采集数据功能，它们通过多跳形式将采集的数据传送到汇聚节点，然后汇聚节点将数据融合到基站，最后将数据发送给需要的用户[1]。无线传感器网络在实际监测应用中，节点要确定自身的位置信息，然后才可以对目标进行准确追踪和定位，如果自身的位置信息不准确，那么其采集的信息不可靠，没有任何实际应用意义[2]。同时由于无线传感器网络节点的规模十分庞大，有时节点达到数以万计，如果采用人工定位或为每一个节点安装一个全球定位系统，成本将相当高，而且网络不易扩展，因此如何设计高精度的传感器节点定位算法，提高无线传感器网络节点性能，具有重要理论和实用价值[3]。

由于无线传感器网络节点定位具有重要实用价值，引起了人们广泛的关注，根据定位机制，节点定位分为两大类：基于测距和非测距的定位[4]。测距定位方法首先计算传感器节点之间的距离或角度信息，然后采用最大似然估计法、三角测量法得到传感器节点的位置信息，它们具有较高的节点定位精度，但通信开销大、计算复杂度高，而传感器节点的能量有限，这样影响整个传感器网络的生存时间[5-7]。无需测距定位方法可以依靠网络连通性信息实现节点位置确定，成本相对较低，而且对硬件要求不高，定位性能受环境因素的影响小，十分适合于大规模传感器网络，可以满足网络应用要求，因此当前传感器节点定位主要采用该类算法，主要包括：Amorphous算法、DV-Hop算法、质心算法以及APIT算法等[8-10]。然而该类算法通过求解方程组进行节点定位，因此，节点间测距误差对节点的定位精度影响相当大，为了降低测距误差，提高节点定位精度，许多学者将群体智能优化算法引入到无线传感器网络的节点定位过程中，如遗传算法、蚁群算法、模拟退火算法、粒子群算法（Particle Swarm Optimization algorithm，PSO）等[11-14]，但这些算法需要锚节点数量相当大，这样导致算法计算量大，传感器节点的定位精度有待进一步提高。

为了提高无线传感器节点的定位精度，提出一种改进粒子群优化算法（Modified Particle Swarm Optimization algorithm，MPSO）的无线传感器网络节点定位方法。首先根据锚节点选择准则，把上一代和当代计算的节点位置均值作为下一代目标节点的参考节点，然后采用改进粒子群优化算法对节点定位结果进行优化，最后在Matlab 2012平台上实现仿真实验。结果表明，相对其他定位算法，改进粒子群算法加快了无线传感器节点定位速度，提高了定位精度。

2 改进粒子群算法的节点定位

2.1 改进粒子群算法

设粒子群优化（PSO）的种群规模为N，每个粒子由位置、速度向量组成，它们分别为：Xi={xi，1，xi，2，…，.xi，D}，Vi={vi，1，vi，2，…，vi，D}，个体最优位置向量：pi={pi，1，pi，2，…，pi，D}，种群当前最优位置为：pg={pg，1，pg，2，…，pg，D}，粒子群在搜索过程中，根据个体和全局最优不断更新其速度和位置，具体为：

式中，ω为惯性权重；C1、C2为学习因子；rand()为随机函数[15]。

在粒子群搜索过程中，粒子经常会处于相对稳定阶段，该阶段搜索速度较慢，全局最优点位置变化很小，如果在PSO算法的搜索后期，粒子极有可能陷入局部极小值，此时粒子飞行速度很慢，若没有外力的干涉，粒子难以逃逸局部极小点。针对该缺陷，本文提出了一种改进粒子群优化（MPSO）算法。通过函数评价结果对粒子进行调整，具体为：

（1）获取稳定阶段前的全局最优点Xex-best。

（2）将粒子Xbest位置设置为当前搜索到的全局最优点的位置，速度设置为0。

（3）将Xbest位置的第i维值替换为Xex-best的第i维值，替换后调用函数评价，如果评价结果优于当前全局最优值，调整结束，不然将第i维值改回原值，继续第i+1维的替换和测试，直到所有维测试完毕。

2.2 迭代节点位置的计算

在无线传感器节点定位过程中，由于外界环境因素的影响，再加上参考节点选择的随机性，传感器定位带来不同程度的误差，计算出的多个节点位置作为参考节点，导致定位误差不断传播，因此本文采用迭代平均算法计算每一代位置信息。

假设t+1代的待定位节点oi的参考节点数为L(L≥3)，并且含K个锚节点，迭代平均算法选择参考节点的原则为：

（1）如果L≤6，那么选择全部参考节点。

（2）如果L＞6，而且K≥6，则随机选择6个锚节点作为参考节点；若K＜6，那么首先选择全部锚节点作为参考点，然后从L-K中随机选择剩余的6-K个节点作为参考节点。

设(x′i，t+1，y′i，t+1)表示t+1代节点oi坐标，其通过MPSO算法计算，计算与t代求出的同一节点oi的坐标(xi，t，yi，t)的平均值，那么最终坐标位置(xi，t+1，yi，t+1)为：

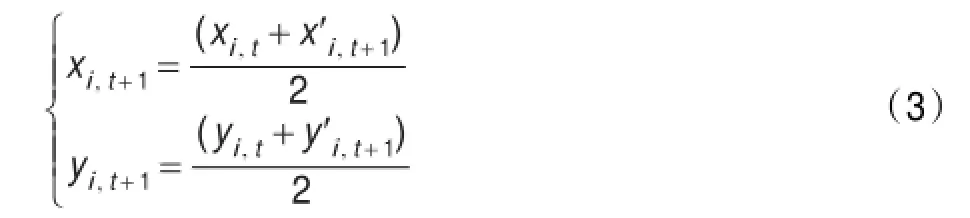
2.3 适应度函数设计

适应度函数用来评价粒子个体的好坏，引导粒子群算法在解空间的搜索方向，具体计算公式为：

式中，m≥3代表目标节点周围的参考节点数；(x，y)表示目标节点坐标，(xi，yi)表示第i个参考节点坐标。

2.4 改进粒子群算法的无线传感器节点定位步骤

步骤1在无线网络监测区域随机部署若干个传感器节点，包括锚节点和待定位节点，锚节点比例较小，它们个数和位置均已知，所有待定位节点间的通信半径相同。

步骤2计算未知无线传感器节点和相邻传感器参考节点之间的距离dˆi。

步骤3采用MPSO算法对未知无线传感器节点的位置进行计算，并得到节点位置与上代位置进行求平均，作为当代节点迭代的位置，然后将自己的位置信息通过无线网络通知其他未知节点。

步骤4计算每一代无线传感器节点的定位误差，具体公式为：

式中，(xi，yi)为未知节点i的实际位置；k表示每代定位的传感器节点数；(xˆi，yˆi)为未知节点的估计位置。

步骤5不断重复步骤2～4，直到达到最大迭代代数，输出所有未知节点的估计位置。

3 仿真实验

3.1 仿真环境

为了测试MPSO算法的无线传感器节点定位性能，在Intel双核2.86 GHz CPU，2 GB的内存，Matlab 2012的平台上进行仿真模拟实验。40个未知传感器节点和若干个锚节点随机分布于100 m×100 m长方形区域，节点通信半径为R。为了使MPSO算法的结果更具说服力，选择标准PSO算法进行对比实验，粒子数为20，最大迭代次数为500，惯性权重ωmax=0.9，ωmin=0.25，粒子最大速度为5 m/s。采用定位误差率对节点定位算法性能进行评价，其计算公式为：

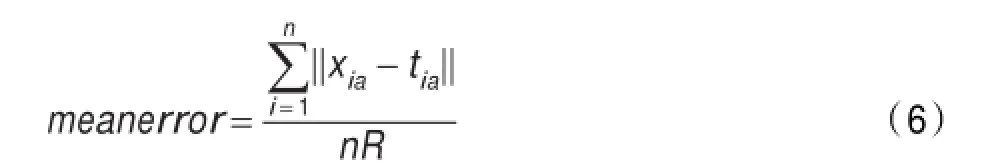
式中，R表示节点通信半径，n表示待定位节点数目。

3.2 结果与分析

3.2.1 定位结果比较

MPSO算法和PSO算法未知传感器节点估计结果如图1所示。从图1可以看出，MPSO算法和PSO算法可以较好地对未知传感器节点的位置进行较正确的估计，但是相对于PSO算法，MPSO算法的节点估计位置与节点实际位置偏差更小，定位精度相对更高，这主要由于MPSO算法利用了每代估算的节点作为参考节点时，节点位置定位误差变小，定位结果更加可靠。

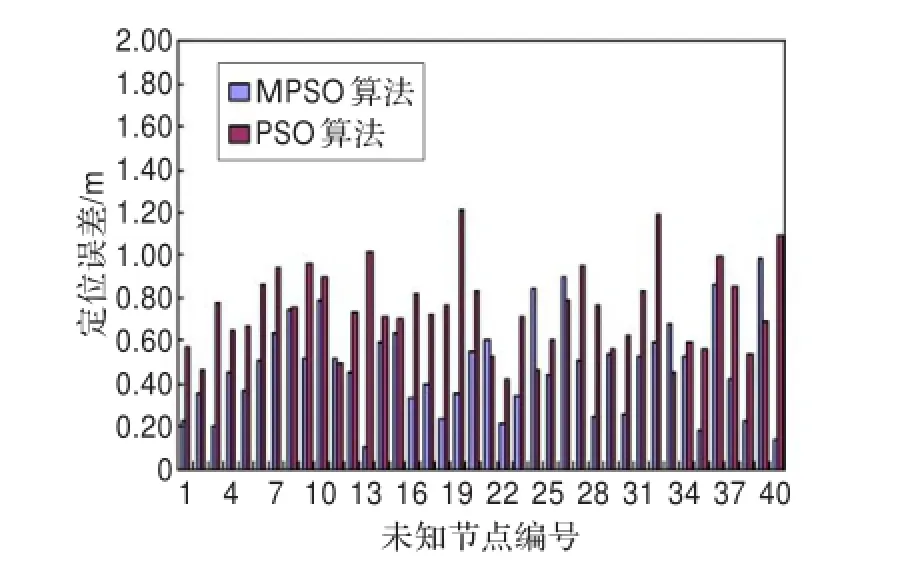
图1 两种算法的估计结果对比

3.2.2 定位速度对比

MPSO算法和PSO算法对未知传感器节点平均定位时间（ms）如图2所示。由图2可清楚地看出，MPSO算法的平均定位时间远远小于PSO算法的平均定位时间，提高了传感器节点的定位速度，这样可以较好地满足无线传感器节点的定位实时性、在线性要求，应用范围更加广泛。

3.2.3 锚节点数对定位误差的影响

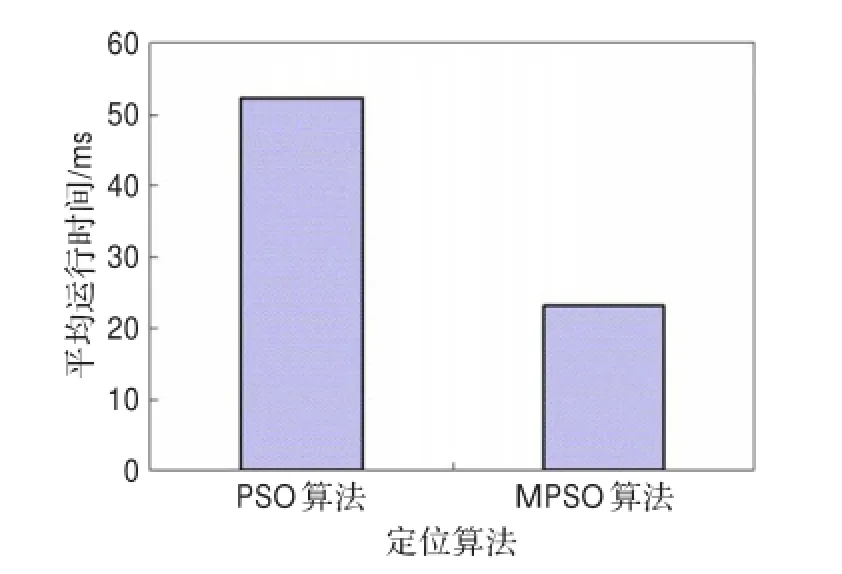
图2 两种算法的定位速度对比

MPSO算法和PSO算法的定位误差与锚节点数的关系如图3所示。从图3可知，当锚节点数等于3时，MPSO算法的定位误差已经到0.5 m以下，而PSO算法在锚节点数为7时，定位误差才达到0.5 m以下，而且随着锚节点个数的增加，无线传感器节点定位精度趋于稳定，可以较好地满足节点定位的实际应用要求。

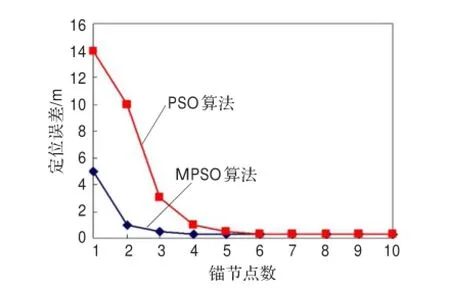
图3 定位误差与锚节点数关系

3.2.4 通信半径对定位精度的影响

在锚节点比例为10%的情况下，MPSO算法和PSO算法平均定位错误与通信半径之间的关系如图4所示。从图4可知，随着通信半径增加，MPSO算法和PSO算法的平均定位误差呈下降趋势，这主要是由于随着通信半径的增大，未知传感器节点的可定位锚节点数增加，同时信号强度增加，测距更加准确，但在相同通信半径情况下，MPSO算法的平均定位误差更小，具有明显的优越性。

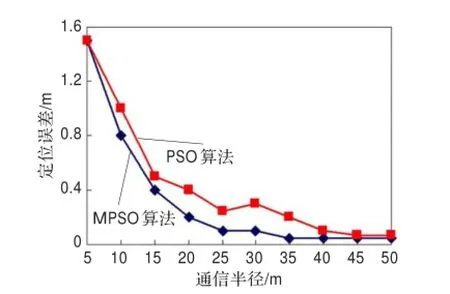
图4 定位误差受通信半径的影响

3.2.5 噪声方差对定位误差的影响

噪声方差的大小影响了节点定位精度，方差值大，说明测距中含有的噪声大，那么优化算法得到的节点位置较真实位置偏差就大，反之偏差小。不同噪声方差条件下，MPSO算法和PSO算法的平均定位误差如图5所示。由图5可知，两种定位算法的定位误差都随噪声方差的增大而增大。相对于PSO算法，MPSO的节点平均定位误差增长相对较慢，这是因为噪声方差增大，引起的测距误差也增大，进而增大节点定位误差，但由于MPSO采用迭代平均思想，减小了每代的定位误差，从而减缓了增长的趋势。

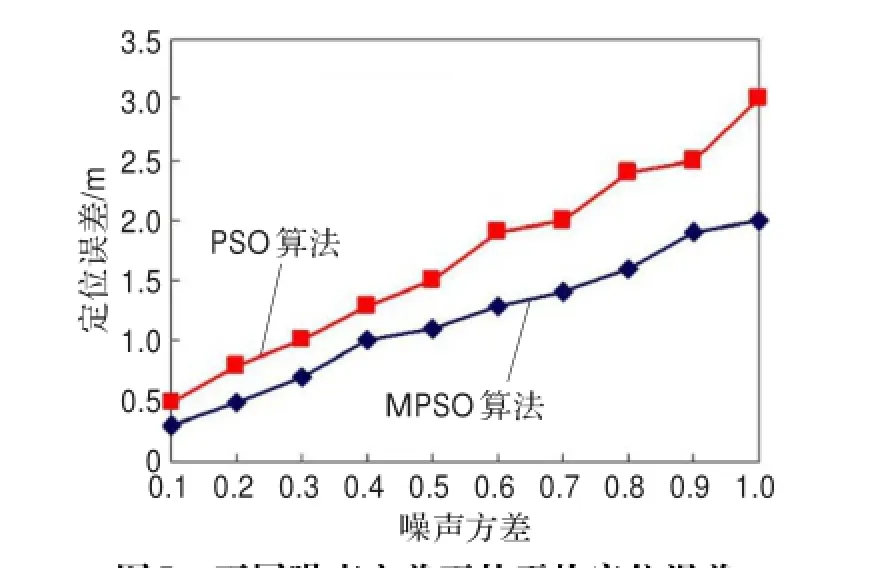
图5 不同噪声方差下的平均定位误差

4 结束语

为了提高无线传感器定位精度，提出一种改进粒子群优化算法的无线传感器节点定位方法，首先根据锚节点选择准则，把上一代和当代节点位置的平均值作为下一代目标节点的参考节点，有效地减少了误差的传播，然后采用改进粒子群优化算法对定位结果进行优化，进一步提高节点定位精度，最后通过仿真实验证明了MPSO算法的有效性和优越性。

[1]周正.无线传感器网络的节点自定位技术[J].中兴通讯技术，2005，11（4）：51-56.

[2]王福豹，史龙，任丰原.无线传感器网络中的自身定位系统和算法[J].软件学报，2005，16（5）：8657-8687.

[3]胡彧，姚维照.基于线性回归的无线传感器加权质心定位算法[J].太原理工大学学报，2011，42（5）：499-502.

[4]Attoungble K J M，Okada K.Localization with Ratio-Distance（LRD）for distributed and accurate localization in Wireless Sensor Networks[J].IEICE Transactions on Communications，2011，94（7）：1944-1951.

[5]陈维克，李文锋，首珩，等.基于RSSI的无线传感器网络加权质心定位算法[J].武汉理工大学学报：交通科学与工程版，2006，30（2）：265-268.

[6]刘瑾.基于测距的无线传感器网络的定位算法的研究[J].航空计算技术，2009，39（6）：124-126.

[7]刘运杰，金明录，崔承毅.基于RSSI的无线传感器网络修正加权定位算法[J].传感技术学报，2009，23（5）：717-721.

[8]周彦，文宝，李建勋.无线传感器网络节点近点加权质心定位方法[J].计算机工程与应用，2012，48（1）：87-89.

[9]Kim S W，Lee J M，Lee J H.Distributed network localization for Wireless Sensor Networks[J].Applied Mathematics&Information Sciences，2012，6（3）：1109-1115.

[10]Zhong Y P，Kuang X H，Huang P W.Improved algorithm for distributed localization in wireless sensor networks[J]. Journal of Shanghai Jiaotong University：Science，2010，15：64-69.

[11]安恂，蒋挺，周正.一种用于无线传感器网络的质心定位算法[J].计算机工程与应用，2007，43（20）：136-138.

[12]Gopakumar A，Jacob L.Localization in wireless sensor networks using particle swarm optimization[C]//IET International Conference on Wireless，Mobile and Multimedia Networks，2008，11：227-230.

[13]Chagas S H，Martins J B，Oliveira L L.Genetic algorithms and simulated annealing optimization methods in Wireless Sensor Networks localization using artificial neural networks[C]//IEEE International Midwest Symposium on MWSCAS，2012：928-931.

[14]赵仕俊，孙美玲，唐懿芳.基于遗传模拟退火算法的无线传感器网络定位算法[J].计算机应用与软件，2009，26（10）：189-192.

[15]陈星舟，廖明宏，林建华.基于粒子群优化的无线传感器网络节点定位改进[J].计算机应用，2010，30（7）：1736-1739.

WANG Yazi,YANG Jianhui

School of Mathematics and Statistics,Zhoukou Normal University,Zhoukou,Henan 466001,China

In order to improve the localization accuracy,a novel localization meothd in wireless sensor network based on improved particle swarm optimization algorithm is proposed.The average of the location of the node in the last generation and the location of the same node in the current generation is regarded as the current generation node location following with the criteria of choosing beacon nodes,and the improved particle swarm optimization algorithm is used to optimize the localization results.The simulation experiments are carried out.The results show that the proposed algorithm not only fastens the localization speed and has improved the localization accuracy effectively compared with the PSO algorithm,so it has wider application range.

wireless sensor networks;Modified Particle Swarm Optimization（MPSO）algorithm;distributed iterative average localization;localization error

为了提高无线传感器节点的定位精度，针对粒子群优化算法存在的问题，提出一种改进粒子群优化算法的无线传感器网络节点定位方法。根据锚节点选择准则，把上一代和当代节点位置的平均值作为下一代目标节点的参考节点，采用改进粒子群算法对节点的定位结果进行优化，在Matlab 2012平台上进行仿真对比实验。仿真结果表明，相对于标准粒子群算法，改进粒子群算法加快了定位速度，提高了无线传感器节点定位精度，应用范围更广。

无线传感器网络；改进粒子群优化（MPSO）算法；分布式迭代平均定位；定位误差

A

TP393

10.3778/j.issn.1002-8331.1402-0079

WANG Yazi,YANG Jianhui.Localization in wireless sensor network based on improved particle swarm optimization algorithm.Computer Engineering and Applications,2014,50（18）：99-102.

周口师范学院青年科学基金重点资助项目（No.zksyqn201310B）；河南省人民政府人才培养联合基金项目（No.U1204618）。

王亚子（1978—），男，讲师，主要研究领域：智能算法、数学建模；杨建辉（1980—），男，讲师，主要研究领域：智能算法、数学建模。

2014-02-13

2014-03-28

1002-8331（2014）18-0099-04