联图W4+Cn的交叉数

岳为君，黄元秋，欧阳章东

1.湖南师范大学数学与计算机科学学院，长沙 410081

2.湖南第一师范学院数学系，长沙 410205

联图W4+Cn的交叉数

岳为君1，黄元秋1，欧阳章东2

1.湖南师范大学数学与计算机科学学院，长沙 410081

2.湖南第一师范学院数学系，长沙 410205

1 引言

本文中未说明的概念和术语均同文献[1]，且无特别说明所涉及的图G=(V(G)，E(G))均指简单连通图，一个图G在平面上的一个好画法是指满足以下四个条件的画法：

（1）任意两条边最多交叉一次；（2）边不能自身交叉；

（3）任意相邻的两条边不能交叉；（4）没有三条边交叉于同一个点。

crD(G)表示在好画法D下G中边与边之间的交叉数目。而图G的交叉数，记为cr(G)，其中cr(G)=，即图G的所有好画法D中交叉数中的最小值。若φ是G的一个好画法，使得crφ(G)=cr(G)，则称φ是G的一个最优画法。

图的交叉数是图的一个重要参数，自从图的交叉数概念提出以来，国内外许多学者都做出了很多的研究，但由于确定图的交叉数是NP-难问题[2]，目前国内外在确定图类的交叉数研究中，主要是针对一些特殊结构的图类上，或者一些图与图作某种运算后得到的图，如完全2-部图Km，n[3]，完全多部图[4-5]一些路，以及星和圈与一些小阶图G的笛卡尔积图[6-11]，特别地，关于完全2-部图Km，n，1954年Zarankiewicz在文献[12]中得到了著名的Zarankiewicz猜想，后来，Ringel和Kainen各自独立发现Zarankiewicz在文献[12]中的猜想有误[13]。D.J.Kleitman在文献[3]中证明了当min{m，n}≤6时，Zarankiewicz猜想成立，即Km，n的交叉数为：cr(Km，n)=Z(m，n)=。这里，对任意实数x，表示不超过x的最大整数。

令G和H是两个没有公共顶点的简单图，图G和H的联图G+H表示这样的一个图：顶点集V(G∪H)=V(G)∪V(H)，边集E(G∪H)=E(G)∪E(H)∪{e(u,v)|∀u∈V(G)且v∈V(H)}，其中e(u，v)表示连接顶点u和v的边。设φ是图G的一个好画法，对G的任意边子集A和B，记号crφ(A)表示在画法φ下，A中边之间产生的交叉数：记号crφ(A，B)表示在画法φ下，A中边与B中的边之间产生的交叉数。显然，当A=E(G)时，crφ(A)=crφ(G)。

本文中，一个轮图Wm是指一个圈Cm添加一个新顶点，并且把这个顶点与圈的所有顶点相连所得的图，记号Cn表示有n个点的一个圈。目前，有关联图的交叉数方面的研究结果较少。Oporowski B等人在文献[14]中得到了联图C3+C6的交叉数。文献[15]已经确定了Pm+Pn和Cm+Cn的交叉数。近期，Klesc M在文献[16]中，得到了所有3-阶和4-阶图G与路Pn，圈Cn的联图的交叉数。本文主要确定了5-阶轮图W4的联图的交叉数，即如下定理：

定理1设W4为轮图，圈Cn为一个长为n的圈，则有：

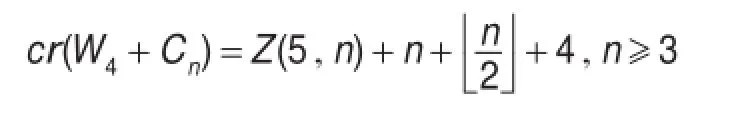
2 基本性质和引理

在证明本文主要结果之前，先给出如下一些基本性质和引理。首先，由交叉数的定义，易有如下性质：

性质2.1令D是图G的一个好画法，且A，B，C是图G的三个边不相交的子图，则有：

（1）crD(A∪B)=crD(A)+crD(B)+crD(A，B)

（2）crD(A∪B，C)=crD(A，C)+crD(B，C)

性质2.2若A是G的子图，则有cr(A)≤cr(G)。

性质2.3若图G与图H同构，则有cr(G)=cr(H)。

引理2.4[11]cr(K4，n)=Z(4，n)，cr(K5，n)=Z(5，n)。

引理2.5[15]设G为任意一个图，φ是Cn+G的一个最优画法，则圈Cn自身不会相交，即crφ(Cn)=0。

引理2.6[16]cr(W3+Cn)=Z(4，n)+n+4，n≥3。

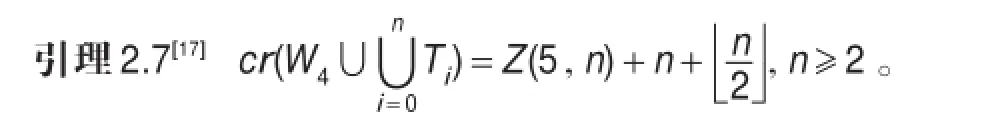
下面的引理在本文第3章主要结果的证明中反复运用。

引理2.8设Cn=v1v2…vn为一个圈，Cn在平面上围成一个圆盘D，在D的内部放置m个点xj(1≤j≤m)，xj与每个vi(1≤i≤n)连边，记这样的边组成的集合为Txj。若φ是这样一个画法，使得所有边集Txj都画在圆盘D的内部，即产生的交叉数，即

3 定理的证明

定理3.1设W4为轮图，圈Cn为一个长为n的圈，则有

在证明定理之前，为了方便，先规定有关记号：设V(W4)={t0，t1，t2，t3，t4}，其中t0是W4的中心点，而ti(1≤i≤4)表示W4的叶子点；V(Cn)={v1，v2，…，vn}，En=E(Cn)；对每个0≤i≤4，记T=T0∪T1∪T2∪T3∪T4，其中Ti={tivj|1≤j≤n}。E′0={t0ti|1≤i≤4}，C4=t1-t2-t3-t4-t1，E(C4)=E′4，则E(W4)=E′0∪E′4。又对于G+Cn的任意边子集A，A表示由G+Cn的边子集A导出的子图。于是W4+Cn的边集可分解为如下一些不相交的边子集的并，即有

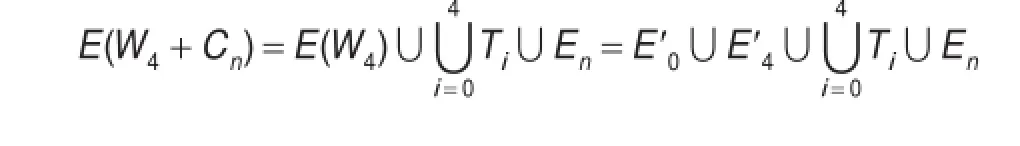
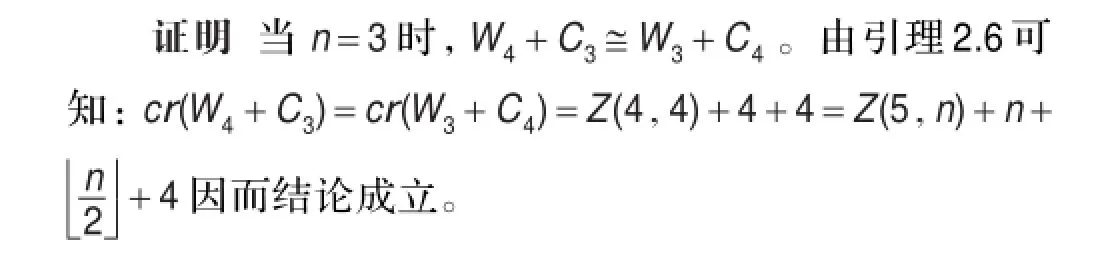
因此，在后面的证明中，总是假定n≥4。

先在平面上构造W4+Cn的一个好画法π，使

画法π的构造如图1。

图1 W4+Cn的一个好画法π

以下证明在画法φ下总能得到一个与式（1）相矛盾的结论，从而得到假设不成立。

在以下的证明，总是记住如下事实及断言：

事实因为φ是最优画法，由引理2.5可知，Cn自身不会交叉，即crφ(En)=0。在画法φ下，Cn围成一个圆盘D，由对称性，可以假定点t0总是位于圆盘D的内部。

断言1在φ是W4+Cn最优画法下，crφ(E′4，En)+

证明根据引理2.7和性质2.1以及事实可得：

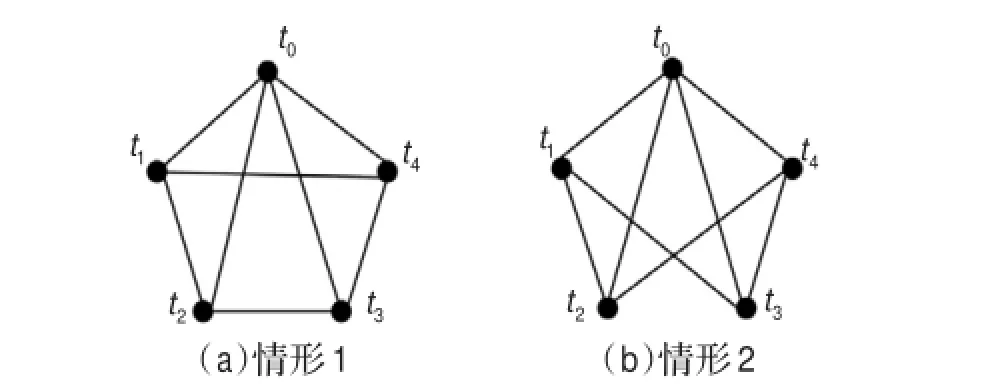
图2 W4的两种特殊情形

子情形1.1当crφ(E′4，En)=0且crφ(E′0，En)≤3时，W4的5个顶点都在Cn的同一区域，且所有边集Txj，0≤j≤4都画在圆盘D的内部，由引理2.8得：

子情形1.2当crφ(E′4，En)=2且crφ(E′0，En)≤1时。

子情形1.2.1当crφ(E′4，En)=2且crφ(E′0，En)=0时，如图3，W4的5个顶点都在Cn的同一区域，且所有边集Txj，0≤j≤4都画在圆盘D的内部，由引理2.8得：

图3 子情形1.2.1

子情形1.2.2当crφ(E′4，En)=2且crφ(E′0，En)=1时，如图4（a）。

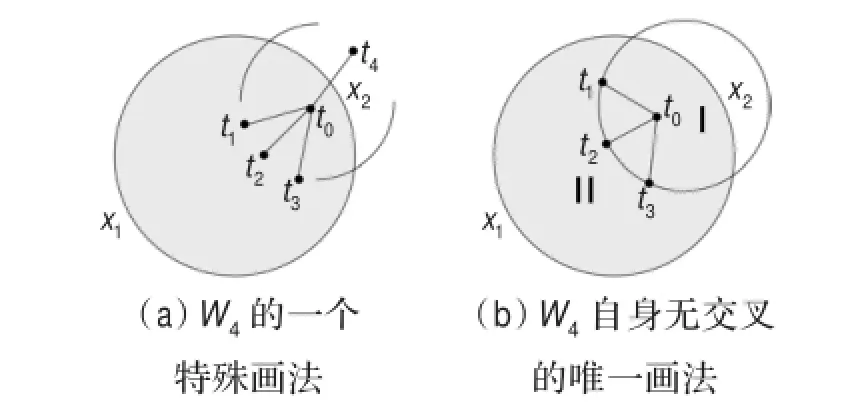
图4 子情形1.2.2

（1）若W4自身有交叉，即crφ(W4)≥1，W4+Cn包含一个K4，n+1子图，则：

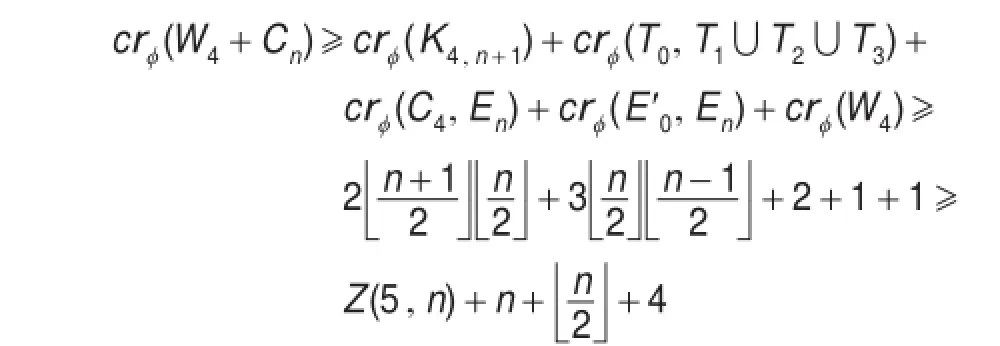
（2）若W4自身无交叉，设Cn有x1个顶点在C4外部，x2个顶点在C4内部，其中x1+x2=n。在最优画法φ下W4+Cn包含一个边导出子图W3+Cn，且crφ(C3，Cn)=2，其中C3=t1-t2-t3-t1。W3的四个顶点全在Cn内部，C3和不自交的Cn有两个交叉只有如图4（b）一种情况，C3把Cn内部分成两个对称区域，若t0在圈C3内部，则t2在圈t1-t0-t3-t1外部，记圈t1-t0-t3-t1为C，若t0在圈C3外部，则t2在圈C内部，由Jordan曲线定理可知crφ(T0，C3)+crφ(T2，C)≥n，由性质2.2知：

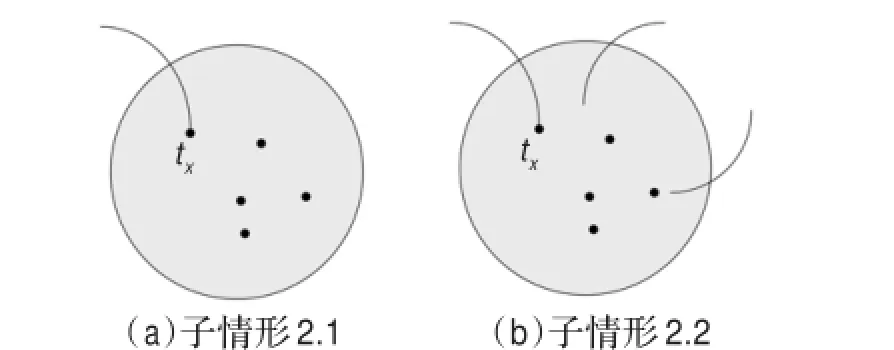
图5 情形2

子情形2.2当crφ(E′4，En)=2时，则crφ(E′0，En)=0如图5（b），记crφ(Tx，En)=1，0≤x≤4。又，W4的四个顶点都在Cn的同一区域，且四个点的所有边集Tx都画在圆盘D的内部，类似子情形2.1易推出与假设矛盾。

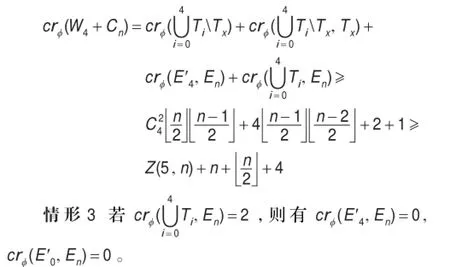
子情形3.1当crφ(Tx，En)=2，0≤x≤4时，满足结论要求，如图6。

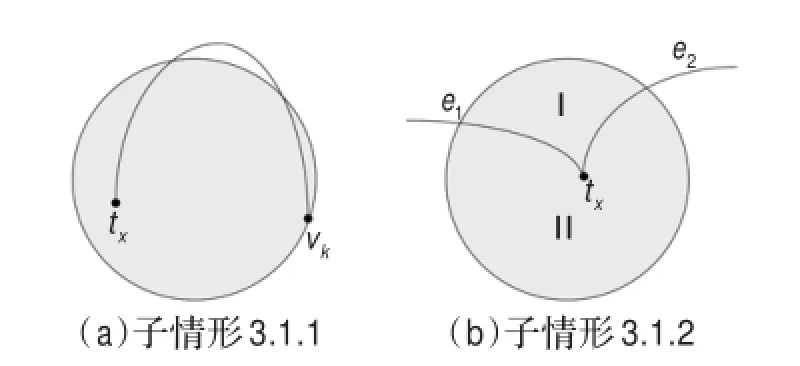
图6 子情形3.1

子情形3.1.1如图6（a），由子情形2.1可得出与假设矛盾。

子情形3.1.2如图6（b），

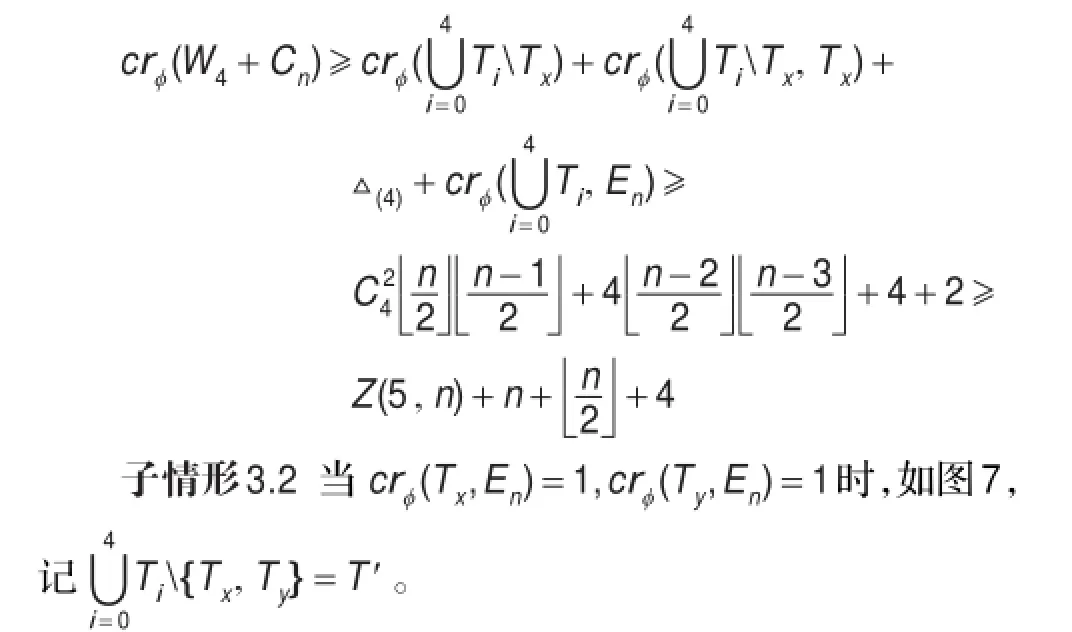
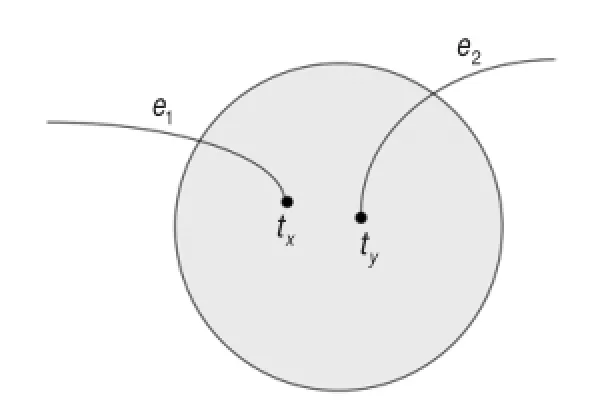
图7 子情形3.2

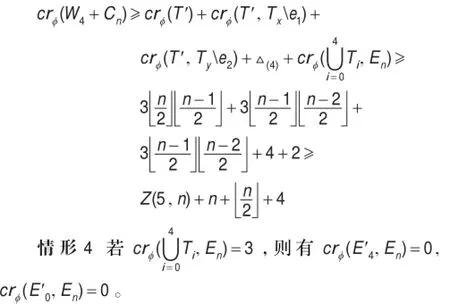
子情形4.1当crφ(Tx，En)=3时，

子情形4.1.1如图8（a），由子情形2.1可得出与假设矛盾。

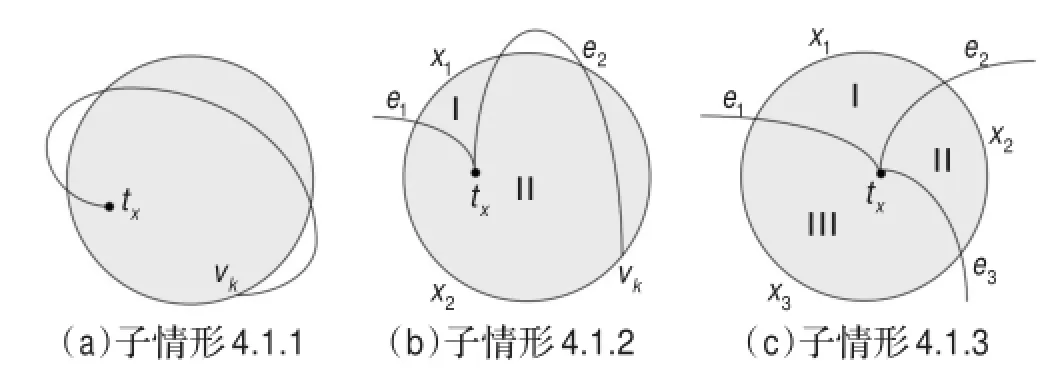
图8 子情形4.1

子情形4.1.2如图8（b），由子情形3.1.2可得出与假设矛盾。

子情形4.1.3如图8（c），

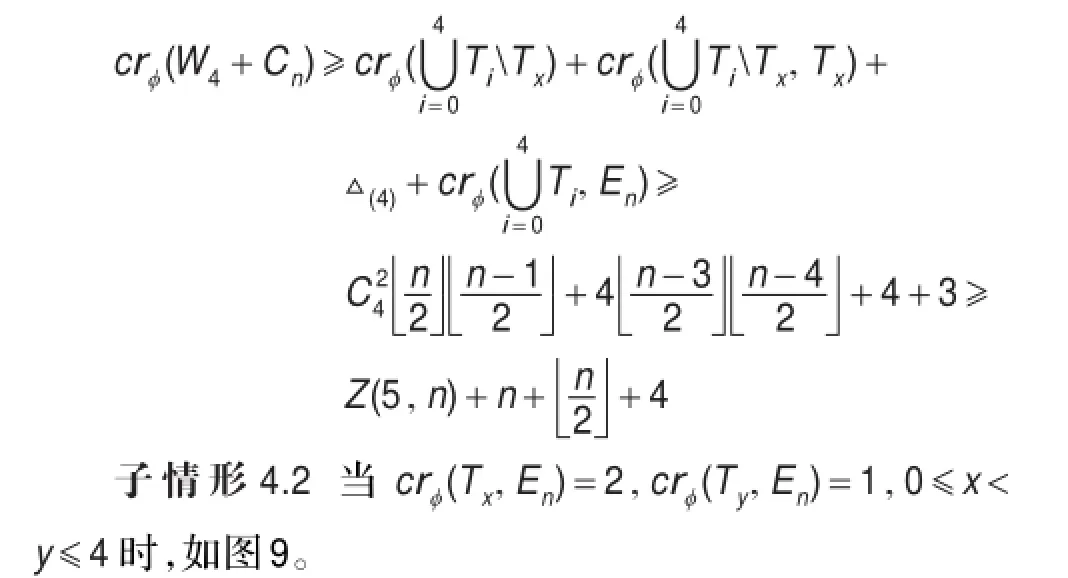
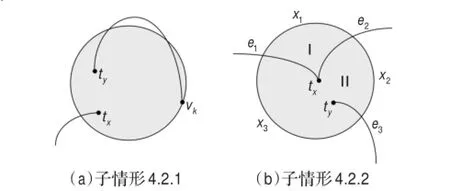
图9 子情形4.2

子情形4.2.1如图9（a），类似子情形3.2可推出与假设矛盾。

子情形4.2.2如图9（b）。

子情形4.2.2.1当crφ(T0,En)=0时，不妨设crφ(T1,En)= 2，crφ(T2，En)=1，则

子情形4.2.2.2当crφ(T0，En)=1，类似子情形4.2.2.1可得出矛盾。

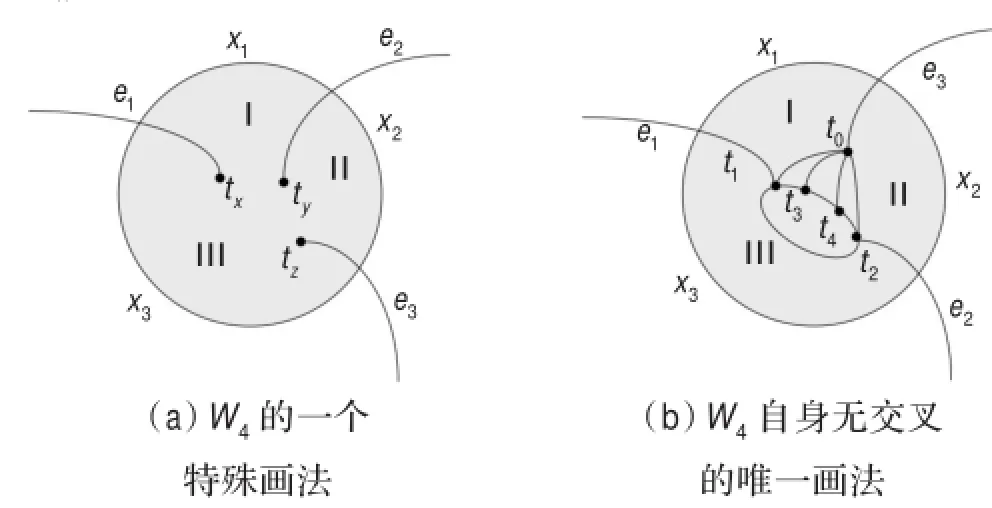
图10 子情形4.3

4 结论及猜想

[1]Bondy J A，Murty U S R.Graph theory with applications[M]. North-Holland：Elsevier Science Ltd，1976.

[2]Garey M R，Johnson D S.Crossing number is NP-complete[J].Slam J Algebric Discrete Methods，1993，4：312-316.

[3]Kleitman D J.The crossing number ofK5，n[J].Combinatorial Theory，1971，9：315-323.

[4]Ho P T.On the crossing number of some complete multipartite graphs[J].Utilitas Mathematica，2009，79：143-154.

[5]Mei H F，Huang Y Q.The crossing number ofK1，5，n[J]. International J Math Com，2007，1：33-44.

[6]Klesc M.The crossing numbers ofK2，3×PnandK2，3×Sn[J].Tatra Moutains Math Publ，1996，1：51-56.

[7]Klesc M.On the crossing number of Cartesian products of stars and paths or cycles[J].Math Slovaca，1991，41：113-120.

[8]Beineke L W，Ringeisen R D.On the crossing number of products of cycles and graphs of order four[J].Graph Theory，1980，4：145-155.

[9]Klesc M.The crossing number of Cartesian products of paths with 5-vertex graphs[J].Discrete Mathematics，2001，233：353-359.

[10]Klesc M.The crossing number of the Cartesian products ofWmwithPn[J].Mathematical Research，2009，29：362-366.

[11]Wang J，Huang Y Q.The crossing number ofK2，4×Pn[J]. Acta Mathematica Scientia：in Chinese，2008，28A：251-255.

[12]Zarankiewicz K.On a problem of P.turan concerning graphs[J].Fund Math，1954，41：137-145.

[13]Guy R K.The decline and fall of Zarankiewicz’s theorem[C]//Proc of the Second Ann Arbor Graph Theory Conference.New York：Academic Press，1969：63-69.

[14]Oporowski B，Zhao D.Coloring graphs with crossing[J]. Discrete Mathematics，2009，309：2948-2951.

[15]Tang L，Wang J，Huang Y Q.The crossing number of the join ofCnandPn[J].International J Math Com，2007，11：110-116.

[16]Klesc M.The join of the graphs and crossing numbers[J]. Discrete Math，2007，28：349-355.

[17]贺佩玲，黄元秋.W4×Sn的交叉数[J].郑州大学学报：理学版，2007，39（4）：14-21.

YUE Weijun1,HUANG Yuanqiu1,OUYANG Zhangdong2

1.College of Mathematics and Computer Science,Hunan Normal University,Changsha 410081,China
2.Department of Mathematics,Hunan First Normal University,Changsha 410205,China

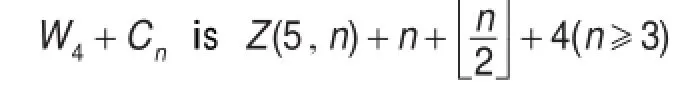
drawing;crossing number;join graph;Cn

联图G+H表示将G中每个点与H中的每个点连边得到的图。在Klesc M.给出联图W3+Cn的交叉数的基础上，应用反证法和排除法得到了联图W4+Cn的交叉数为，并在Zarankiewicz猜想成立的前提下，根据证明，提出对Wm+Cn的交叉数的一个猜想：

画法；交叉数；联图；圈

A

O157.5

10.3778/j.issn.1002-8331.1401-0203

YUE Weijun,HUANG Yuanqiu,OUYANG Zhangdong.On crossing numbers of join ofW4+Cn.Computer Engineering and Applications,2014,50（18）：79-84.

国家自然科学基金（No.11371133，No.11301169）。

岳为君（1989—），男，硕士，主要研究方向：图论及其应用；黄元秋（1966—），通讯作者，男，博士，教授，博士生导师，主要研究方向：图论及其应用；欧阳章东（1981—），男，博士，讲师，主要研究方向：图论及其应用。E-mail：hyqq@hunnu.edu.cn

2014-01-14

2014-03-18

1002-8331（2014）18-0079-06