用Pb-2 Ritz法分析矩形板在不同边界条件下自由振动时的精度

路一

（安徽新华学院土木与环境工程学院，安徽 合肥 230088）

用Pb-2 Ritz法分析矩形板在不同边界条件下自由振动时的精度

路一

（安徽新华学院土木与环境工程学院，安徽 合肥 230088）

弹性支承板模型作为在工程结构分析中常用的结构模型广泛应用于土木工程、机械、电子工程、交通运输、航空航天工程中及轻工工程中，而弹性支撑板在工程上主要指柱支承板.经典的板理论不可避免的导致一些错误,所以必须引用计入剪切变形效应的中厚板理论.应用pb-2R itz法分析具有弹性边界即不同边界条件下的矩形中厚板的自由振动问题很少见到有文章发表，本文主要用来验证Pb-2 Ritz法的精确性和收敛性，为研究其他不同的约束条件下板的自由振动提供参考.

中厚板；Pb-2 Ritz法；自由振动

1 研究现状

板壳结构广泛地应用于工程中，随着我国国民经济持续、快速发展，交通运输和城市基础设施的建设日益受到重视，关系着整个结构建设的安全、稳定的板壳结构尤为重要.板壳结构分析是现代固体力学中的一个分支,近几十年,随着科学技术的突飞猛进,其发展异常迅速.弹性支承板模型是一种在工程结构分析中广泛应用的结构模型，对弹性支承板的分析40多年来也一直是工程师所关心的问题.弹性支撑板在工程上是种典型结构.

在克希霍夫薄板理论假设下，忽略的z方向上的剪切变形和转动惯量会产生很大误差，从而导致危险设计.而中厚板理论能够突破薄板理论的局限性，在分析中等厚度板时具有简单性和精确性.

国外杂志中，Liew等（1996）应用pb-2 Ritz法研究了任意四边形厚板的自由振动问题.W.Karunasena等（1997）应用pb-2 Ritz法研究了一般三角形板考虑剪切变形的自由振动问题.F.-L.Liu等（1999）应用微分求积单元法分析了具有混合边界的矩形中厚板的自由振动问题.D.Zhou（2001，2002）应用pb-2 Ritz法和铁木辛哥梁单元理论分析了具有弹性支座支撑的明德林板的自由振动问题和应用一系列变化梁函数来分析具有点支撑且厚度变化的矩形板的自由振动问题.Lanhe Wu等（2005）应用微分容积法分析了任意形状中厚板的自由振动问题.

2 矩形板在不同边界条件下的精度分析

分析一：考虑与文献[1,4]相同条件的四边简支（SSSS）的矩形板的振动，四边简支边界表达式中的幂指数S1，S2，S3，S4为1，其余为0，定义无因次固有频率t=0.001a.计算结果分别列于表1，与文献[1，4]结果精度比较绘于图1.

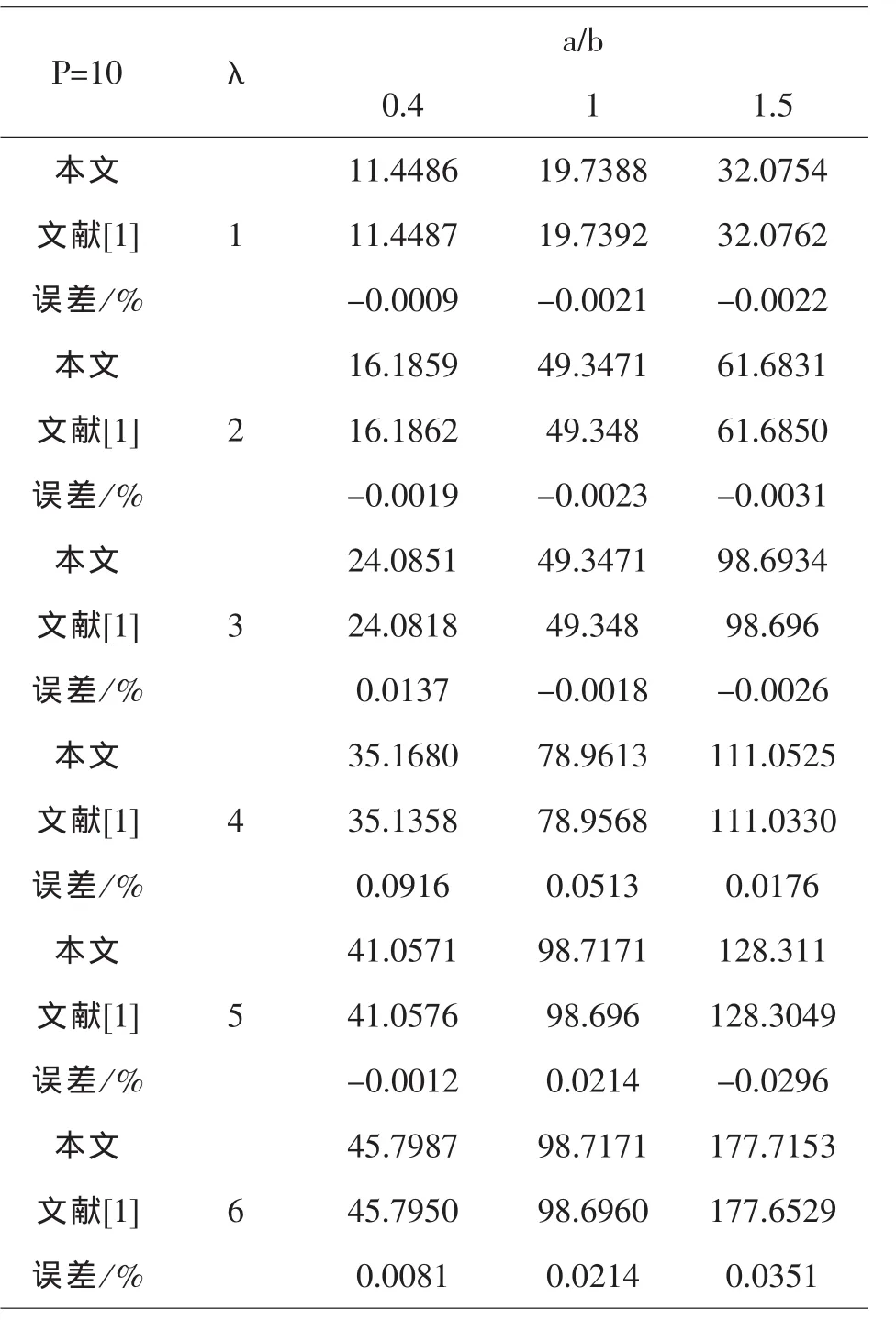
表1 四边简支薄板自由振动的固有频率

由表1和图1可以知道，当板厚t/a=0.001时，本文四边简支时矩形板的固有频率结果收敛较快，而且当随着长宽比的逐渐增大各阶频率系数也逐渐增大.

分析二：为了验证方法的收敛性和有效性，考虑与文献[1,4]相同条件的四边固定（CCCC）的矩形板的振动，四边固定时边界表达式中的幂指数Si为1.板的几何尺寸板长为a板宽为b,定义无因次固有频率为质量密度，D为板的抗弯刚度，ω为固有频率.板厚度分别取t=0.2a.其中表2相当于文献[1，4]中四边弹簧时Sw=108，SΦ=108的情况.计算结果分别列于表2，与文献[1,4]结果精度比较分别绘于图2.

由表2和图2可以知道，当板厚t/a=0.001时，p=10时本文四边固定时矩形板的固有频率已和文献[1,4]的结果符合较好；从图2可以看出无量纲固有频率随着长宽比的逐渐增大各阶频率系数也逐渐增加.

图1 四边简支薄板（t/a=0.001）无量纲固有频率精度比较（a/b=0.4）

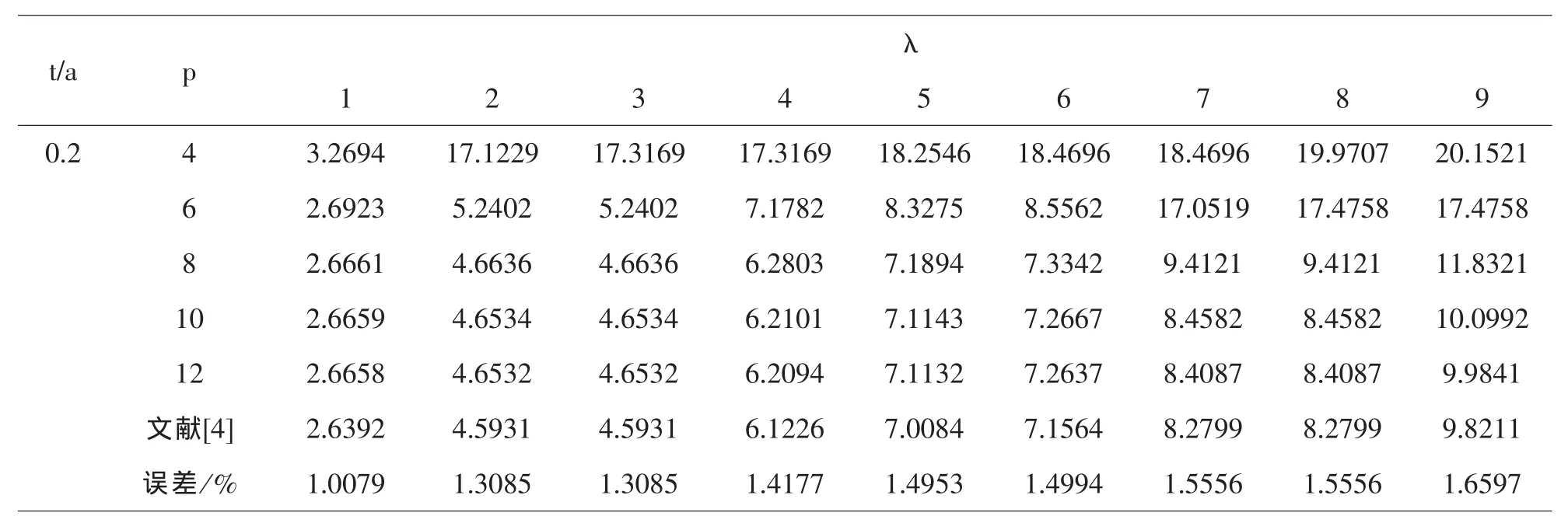
表2 四边固定厚板自由振动的固有频率

图2 四边固定厚板（t/a=0.2）无量纲固有频率精度比较

由表2和图2可以知道，当板厚t/a=0.2时，p=8开始本文四边固定时矩形厚板的固有频率结果收敛较快，当p=10时本文结果符合较好.

以上算例表明，本文方法对计算不同边界条件下支承的矩形板的固有频率有优良的数值精度.

〔1〕LEISSA A W.The free vibration of rectangular plates [J].Journal of Sound and Vibration,1973,31(3):257-293.

〔2〕W.Karunasena and S.Hittipornohai Free vibration of shear-deformable general triangular plates Journal of Sound and Vibration 1997,199(4)：595-613.

〔3〕Y.Xiang,K.M.Liew and S.Kitipornchai Vbration analysis of rectangular Mindlin plates resting on elastic edge suppors Journal of Sound and Vibration 1997,204(1)：1-16.

〔4〕XIANG Y,LIEW K M,KITIPORNCHAI S.Vbration analysis of rectangular Mindlin plates resting on elastic edge suppors[J].Journal of Sound and Vibration,1997, 204(1):1-16.

TU311

A

1673-260X（2014）07-0051-02

2013年安徽高校省级优秀青年人才基金项目（KJ2013Z106）；2012年度国家级创新创业训练计划创新训练项目（201212216007）