Hom-Leibniz Superalgebras

SHEN Zhen-jun,WEI Zhu,ZHANG Qing-cheng

(Mathematics and Statistics,Northeast Normal University,Jilin 130024,China)

Hom-Leibniz Superalgebras

SHEN Zhen-jun,WEI Zhu,ZHANG Qing-cheng

(Mathematics and Statistics,Northeast Normal University,Jilin 130024,China)

We gived the def i nition of Hom-Leibniz superalgebra and studied its basic properties.In particular,the derivations of Hom-Leibniz Superalgebras are portrayed in detail.

Hom-Leibniz superalgebras;derivations;basic properties

§1.Introduction

The theory of Hom-algebras originated from the introduction of the notion of a Hom-Lie algebras by J T Hartwig,D Larsson and S D Silvestrov in[1],in the study of algebraic structures describing some q-deformation of the Witt and the Virasoro algebras.Hom-Lie superalgebras and other Hom-algebras structures have been widely investigated these last years,a Hom-Lie superalgebra is a triple(G,[·,·],α),which G is a vector superspace,α is a endomorphism of G and the skew-symmetric bracket satisf i es an α-twisted variant of the Jacobi identity,Lie algebras are special cases of Hom-Lie algebras in which α is the identify map.Hom-Lie superalgebras were studied in[3]and cohomology theory of Hom-Lie superalgebras and Hom-leibniz algebras were studied in[9,11,13].The concept of Leibniz algebras was f i rst introduced by Loday[2]in the study of the so-called Leibniz homology of Lie algebra as a“noncommuctive”analog of Lie algebra homology found by Cuvier[4]and Loday[5]respectively.And the concept of Leibniz superalgebras and its cohomology were f i rst introduced by Dzhumadil’daev in[6],some theory of superdialgebras and Leibniz superalgebra and their cohomology were studied in[7-8]and the central extensions,the universal central extensions of Leibniz superalgebras were constructed. The purpose of this paper is to study the basic properties of Hom-Leibniz superalgebras,and portrayed derivations of Hom-Leibniz superalgebras.

§2.The Basic Properties of Hom-Leibniz Superalgebras

In this section,we f i rst recall the notion of Hom-Leibniz superalgebras and then give some construction of the Hom-Leibniz superalgebras.

Def i nition 2.1A Hom-Leibniz superalgebra is a triple(G,[·,·],α)consisting of a superspace G,an even bilinear map(bracket)[·,·]:G×G→G and an even superspace homomorphism α:G→G satisfying

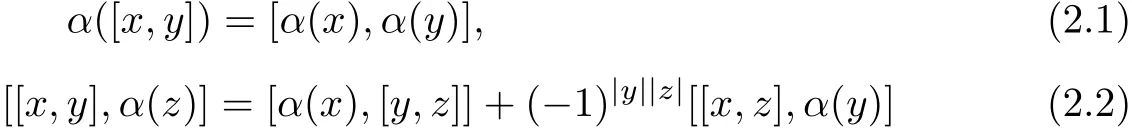
for all homogeneous elements x,y,z∈G.

When α=Id,we call G is a Leibniz superalgebra.The identity(2)is called Hom-Leibniz superidentity.

Proposition 2.2Given two Hom-Leibniz superalgebras(G,[·,·],α)and(V,[·,·],β)and there is a Hom-Leibniz superalgebra(G⊕V,[·,·],α+β),where the bilinear map[·,·]:(G⊕V)⊗2→G⊕V is given by

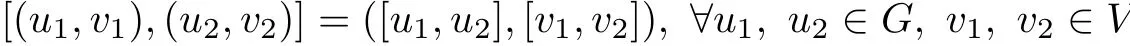
and the even multiplicative superspace homomorphism α+β:G⊕V→G⊕V is given by

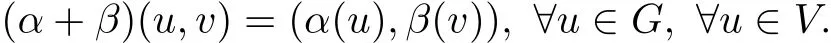
ProofWe just check that α+β is an even superspace homomorphism and(G⊕V,[·,·],α+β) satisf i es the Hom-Leibniz superidentity.In fact,we can obtain

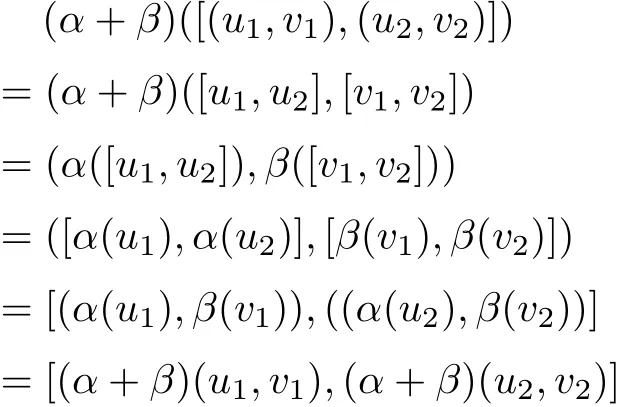
and

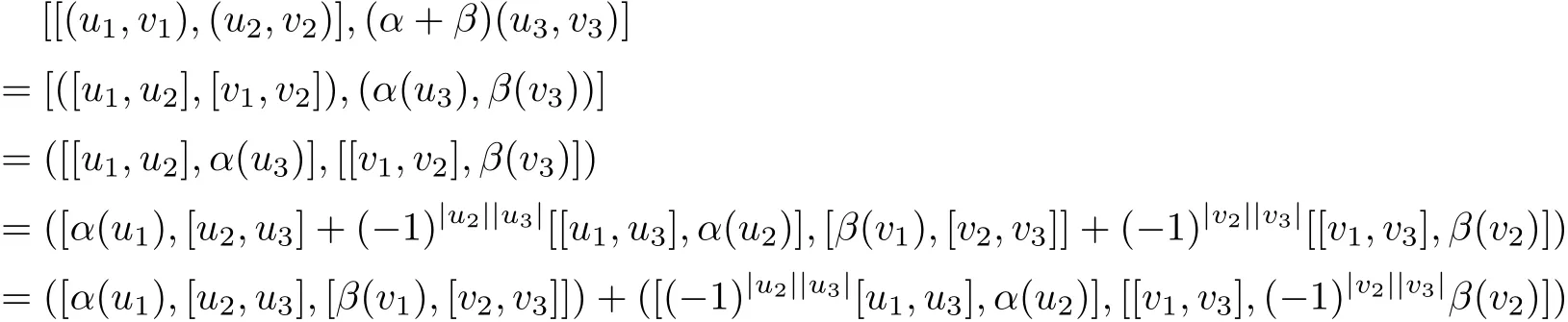
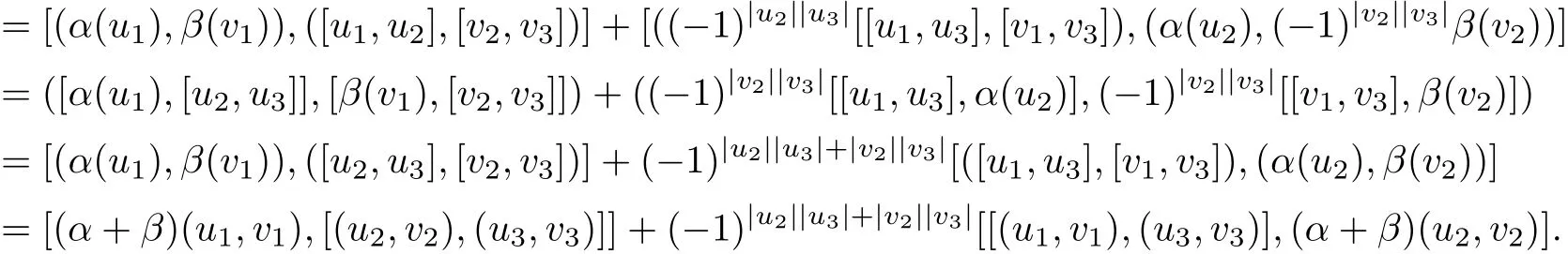
Therefore,(G⊕V,[·,·],α+β)is a Hom-Leibniz superalgebra.

Def i nition 2.3Let(G,[·,·],α)and(V,[·,·],β)be two Hom-Leibniz superalgebras.An even homomorphism φ:G→V is said to be a morphism of Hom-Leibniz superalgebras if satisfying

for anyµ,ν∈G.

Denote by ħφ={(u,φ(u)|u∈G}.

Proposition 2.4A linear map φ:(G,[·,·],α)→(V,[·,·],β)is a morphism of Hom-Leibniz superalgebras if and only if the graph ħφ⊂G⊕V is a Hom-Leibniz sub-superalgebra of (G⊕V,[·,·],α+β).

ProofLet φ:(G,[·,·],α)→(V,[·,·],β)be a morphism of Hom-Leibniz superalgebras,then for any u1,u2∈G,we have

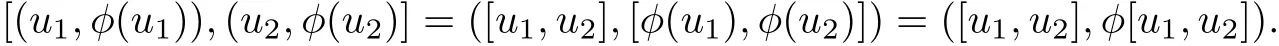
Thus the graph ħφis closed under the bracket operation[·,·].Furthermore,by(4),we have

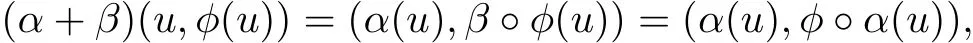
which implies that(α+β)(ħφ)⊂ħφ.Thus ħφis a Hom-Leibniz sub-superalgebras of(G⊕V,[·,·],α+β).

Conversely,if the graph ħφ⊂G⊕V is a Hom-Leibniz sub-superalgebra of(G⊕V,[·,·],α+β), then we have

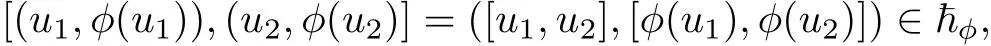
that is

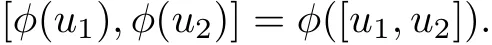
Furthermore,(α+β)(ħφ)⊂ħφyields that

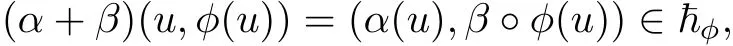
which is equivalent to the condition β◦φ=φ◦α.Therefore φ is a morphism of Hom-Leibniz superalgebras.

Proposition 2.5Let(G,[·,·])be a Leibniz superalgebra and α:G→G be an even Leibniz superalgebra endomorphism.Then(G,[·,·]α,α),in which[·,·]α=[α(x),α(y)]is a Hom-Leibnizsuperalgebra.Moreover,it is supposed that(G′,[·,·]′)is another Leibniz superalgebra and α′:G′→G′is an even Leibniz superalgebra endomorphism,and if f:G→G′is a Leibniz superalgebrsa morphism that satisf i es f◦α=α′◦f,then

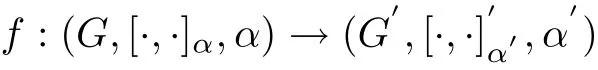
is a morphism of Hom-Leibniz superalgebras.

ProofWe show that the(G,[·,·]α,α)satisf i es the Hom-Leibniz superidentity.Indeed

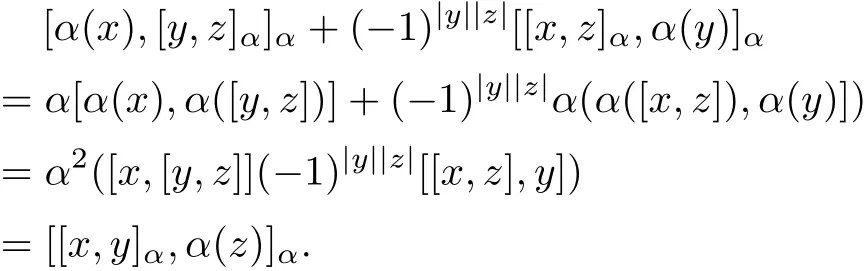
The second assertion follows from

Example 2.6Let G=G¯0⊕G¯1be a 2-dimensional superspace,where G¯0is generated by e1and G¯1is generated by e2.The triple(G,[·,·],α)is a Hom-Leibniz superalgebra def i ned by[e2,e1]=ke2with α(e1)=e1,α(e2)=ke2.

Example 2.7Let G=G¯0⊕G¯1be a 3-dimensional superspace,where G¯0is generated by e1,e2and G¯1is generated by e3.The triple(G,[·,·],α)is a Hom-Leibniz superalgebra def i ned by[e2,e2]=e1,[e3,e2]=4e3with α(e1)=e1,α(e2)=e1+e2,α(e3)=2e3.

Theorem 2.8Let(G,[·,·],α)be a Leibniz superalgebra and β:G→G be an even Leibniz superalgebra endomorphism.Then(G,[·,·]β,β◦α)is a Hom-Leibniz superalgebra, where[x,y]β=β([x,y]).

ProofFor all x,y,z∈G,we have

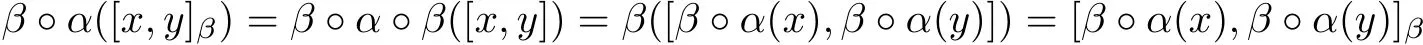
and

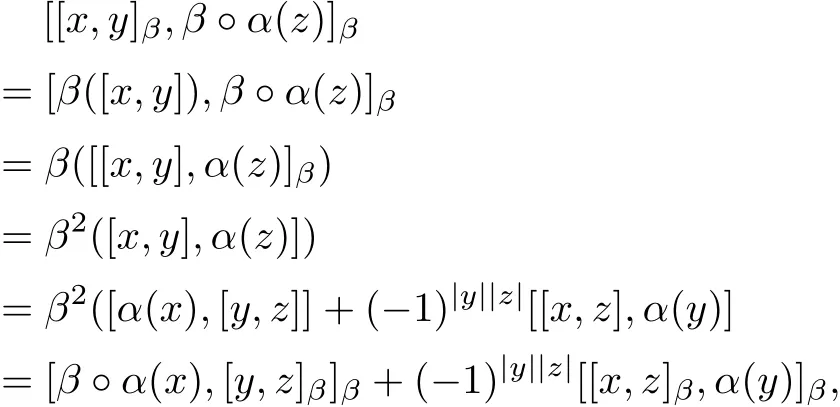
so(G,[·,·]β,β◦α)satisf i es the Hom-Leibniz superidentity.Therefore,(G,[·,·]β,β◦α)is a Hom-Leibniz superalgebra.

RemarkWhen α=Id,that is Proposition 2.5.

§3.Derivations of Hom-Leibniz Superalgebras

Let(G,[·,·],α)be a Hom-Leibniz superalgebra,denoting by αkthe k-times composition of α,i.e.,αk=α◦α···◦α(k-times).In particular,α−1=0,α0=Id,α1=α.

Def i nition 3.1For any k≥−1,we call D∈(EndG)i,where i∈Z a αk-derivation of the Hom-Leibniz superalgebra(G,[·,·],α),if

and

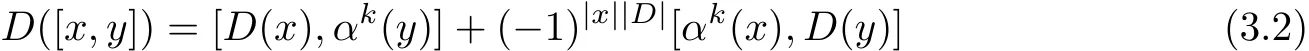
for all homogeneous elements x,y∈G.

We denote by Derαk(G)=(Derαk(G))¯0⊕(Derαk(G))¯1the set of αk-derivations of the Hom-Leibniz superalgebra(G,[·,·],α)and

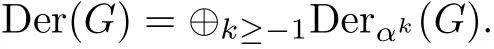
For any homogeneous element a∈G,satisfying α(a)=a,def i ne adk(a)∈End(G)by

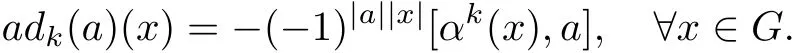
Notion that adk(a)and a are of the same parity.

Theorem 3.2Let(G,[·,·],α)be a Hom-Leibniz superalgebra.Then adk(a)is an αk+1-derivation,which we call inner αk+1-derivation.

ProofIndeed we have

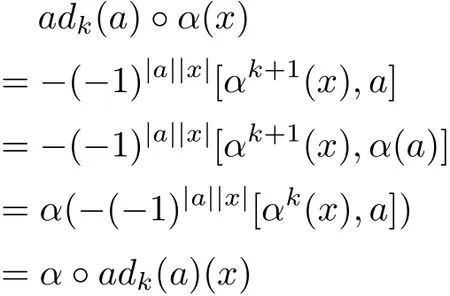
and

Therefore,adk(a)is a αk+1-derivation.

We denote by Innαk(G)the set of inner αk-derivations,i.e.,

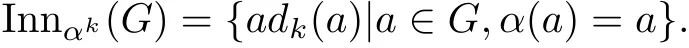
For any D∈Der(G)and D′∈Der(G),def i ne their commutator[D,D′]as usual

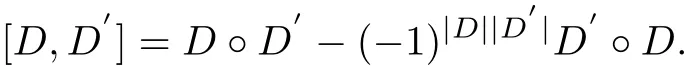
Lemma 3.3For any D∈(Derαk(G))iand D′∈(Derαs(G))j,where k+s≥−1 and (i,j)∈Z22,we have

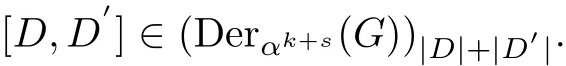
ProofFor any x,y∈G,we have

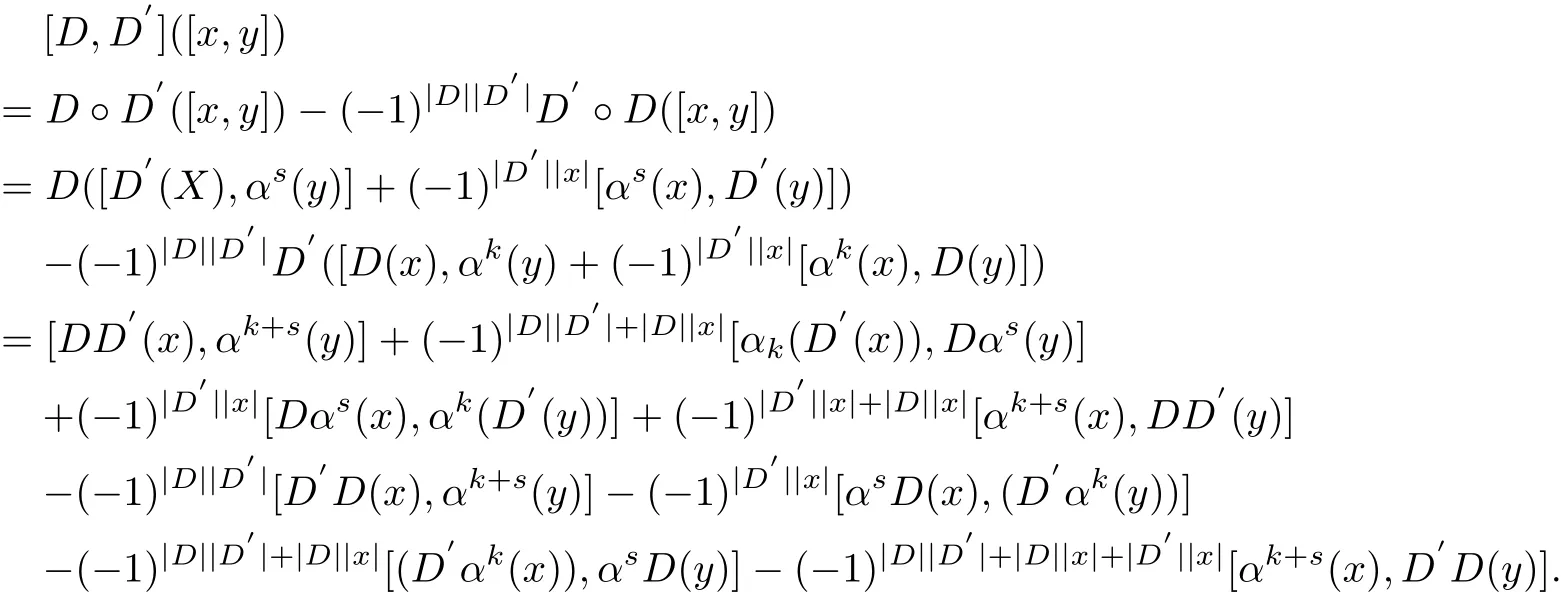
Since D and D′satisfy α◦D=D◦α and α◦D′=D′◦α,we have

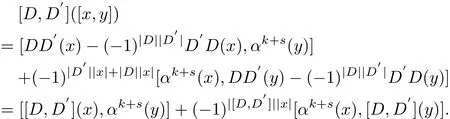
It is easy to verify that α◦[D,D′]=[D,D′]◦α,which leads to[D,D′]∈Derαk+s(G))|D|+|D′|.

RemarkObviously,we have

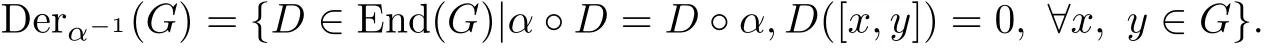
Thus for any D,D′∈Derα-1(G),we have[D,D′]∈Derα-1(G).

Proposition 3.4With the above notations,when α satisf i es α2=α and(Der(G),[·,·],α′) is a Hom-Leibniz superalgebra,in which the bracket[·,·]is def i neted by

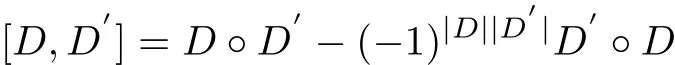
and

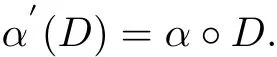
ProofFor any x,y∈G,D∈Der(G),we have

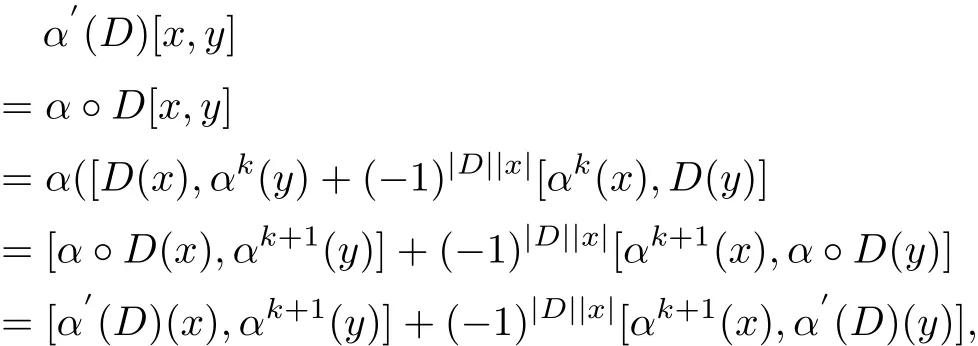
that is α′(D)∈(Derαk+1(G)).Then we show that α′is a homomorphism.Indeed

For any D1,D2,D3∈Der(G),we have

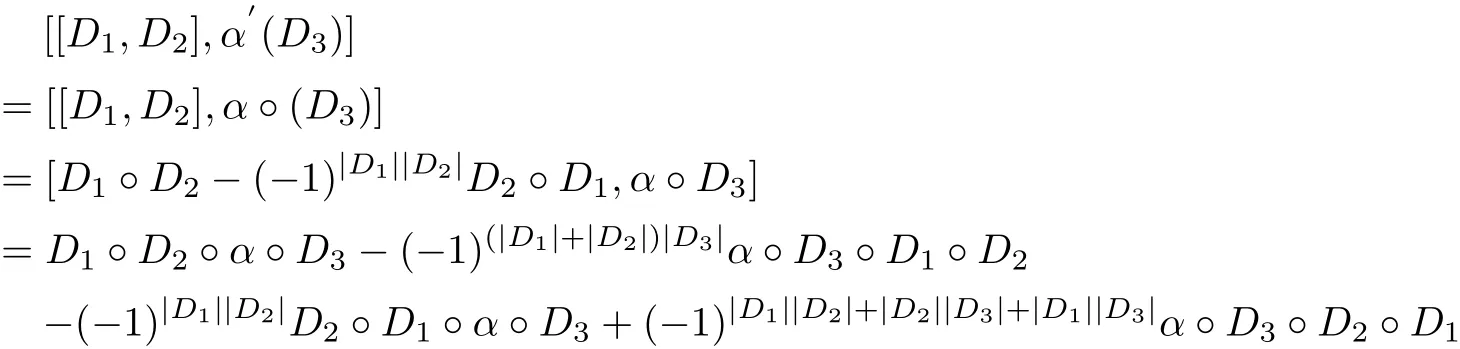
and

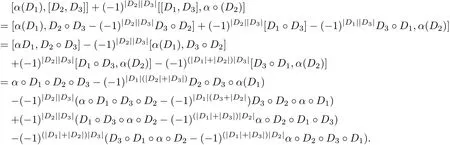
Since α◦D1=D1◦α,α◦D2=D2◦α,α◦D3=D3◦α,so

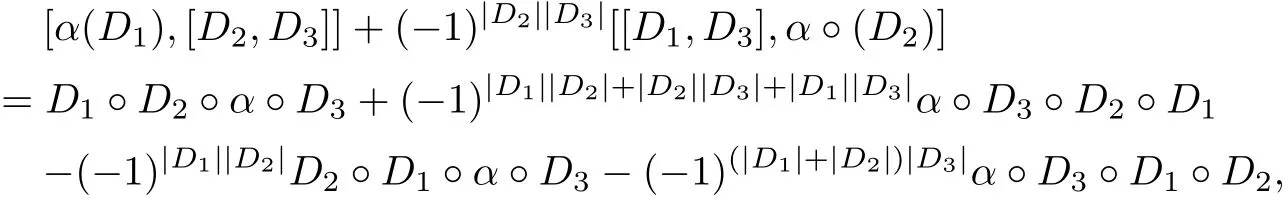
that is,[[D1,D2],α′(D3)]=[α(D1),[D2,D3]]+(−1)|D2||D3|[[D1,D3],α◦(D2)].We know that (Der(G),[·,·],α′)is a Hom-Leibniz superalgebra.

RemarkWhen omitting the condition α2=α,we know that Der(G)is a Leibnizsuperalgebra.

Finally,we consider extensions of Hom-Leibniz superalgebra(G,[·,·],α)using derivations. For any D∈Der(G),consider the vector space˜G=˜G¯0⊕˜G¯1,where˜G¯0=G¯0⊕ℝD,˜G¯1=G¯1ℝ is a real f i eld.Def i ne a skew-symmetric bilinear bracket operation[·,·]Don˜G by

[µ+mD,ν+nD]D=[µ,ν]+mD(ν)−(−1)|D||µ|nD(µ),∀µ,ν∈G,m,n∈ℝ.

Def i ne αD∈End(G⊕ℝD)by αD(µ+mD)=α(µ)+mD.

Theorem 3.5With the above notions,(˜G,[·,·]D,αD)is a Hom-Leibniz superalgebra if and only if D is an α-derivation of the Hom-Leibniz superalgebra(G,[·,·],α).

ProofFor anyµ,ν∈G,n,m∈ℝ,we have

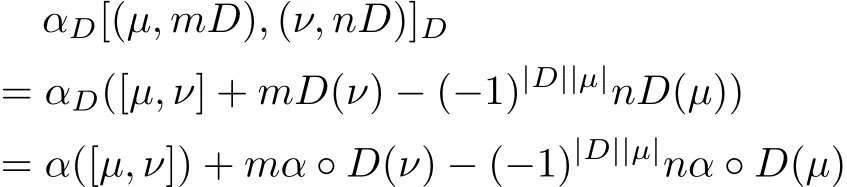
and

Since α is a morphism of Hom-Leibniz superalgebra,thus αDis a morphism of Hom-Leibniz superalgebra,D◦α=α◦D,then αD[(µ,mD),(ν,nD)]D=[αD(µ,mD),αD(ν,nD)]D.On the other hand,we can get

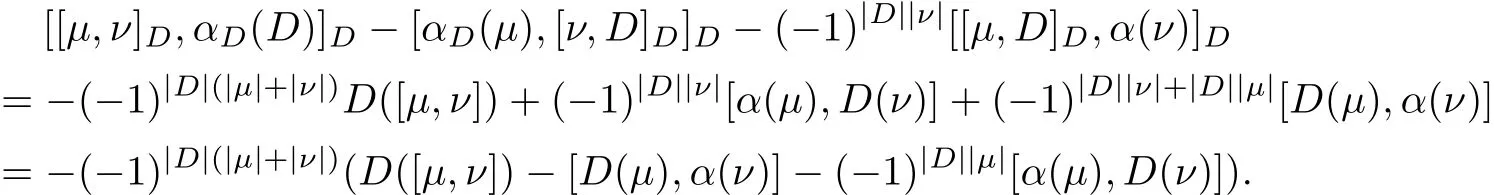
Therefore,it is obvious that the Hom-Leibniz superidentity is satisf i ed if and only if

Thus(˜G,[·,·]D,αD)is a Hom-Leibniz superalgebra if and only if D is an α-derivation.

[1]HARTWING J,LARSSON D,SILVESTRV S.Deformations of Lie algebras using σ-derivations[J].J Algebra, 2006,295:314-361.

[2]LODAY J.Une version non commutative des algebras de lie:Les algebras de Leibniz[J].Enseign Math, 1993,39:269-294.

[3]YAU D.Hom-algebras and homology[J].Lie Theory,2009,19:409-421.

[4]CUVIER C.Homologie de Leibniz et homologie de hochschild[J].C R Acad Sci Paris,1991,313:569-572.

[5]LODAY J.Cup-product for Leibniz cohomogy and dual Leibniz algebras[J].Math Scand,1995,77:189-196.

[6]DZHUMADIL’DAEV A.Cohomologies of colour Leibniz algebras:Pre-simplicial approach,Lie theory and applications in physics[J].Preceeding of the Third International Workshop,1999:124-135.

[7]LIU Dong,HU Nai-hong.Leibniz superalgebras and central extensions[J].J Algebra Appl,2006,5:765-780.

[8]LIU Dong.Steinberg Leibniz algebras and superalgebeas[J].J Algebra,2005,283:199-221.

[9]FAOUZI A,ABDENACER M,NEJIB S.Cohomology of Hom-Lie superalgebras and q-deformed Witt superalgebra[J].arXiv:1204,6244:2012.

[10]SHENG Yun-he.Representions of Hom-Lie algebras[J].arXiv:1005,0140:2010.

[11]CHENG Yong-sheng,SU Yu-cai.(Co)Homology and universal central extension of Hom-Leibniz algebra[J]. Acta Mathematica Sinica,2011,27:813-830.

[12]YAU D.Non-commutative Hom-Poisson algebra[J].arXiv:1010,3408:2012.

[13]CHENG Yong-sheng,YANG Heng-yun.Low-dimensional cohomology of q-deformend Heisenberg-Virasoro algebra of Hom-type[J].Front Math China,2010,5:607-622.

tion:16E40,17B56,17B68,17B70

1002–0462(2014)04–0583–09

date:2013-03-11

Supported by the National Natural Science Foundation of China(10871057,11171055)

Biographies:SHEN Zhen-jun(1986-),male,native of Xinyang,Henan,a M.S.D.of Northeast Normal University,engages in Lie algebras and Lie superalgebras;ZHANG Qing-cheng(1960-),male,native of Xinyang, Henan,a professor of Northeast Normal University,engages in Lie superalgebras(corresponding author).

CLC number:O125.5Document code:A