Rectangular Ring Congruences on an E-inversive Semiring
CHENG Zi-qiang,ZHOU Yuan-lan,PAN Shi-ju
(Department of Mathematics,Jiangxi Normal University,Nanchang 330022,China)
Rectangular Ring Congruences on an E-inversive Semiring
CHENG Zi-qiang,ZHOU Yuan-lan,PAN Shi-ju
(Department of Mathematics,Jiangxi Normal University,Nanchang 330022,China)
In this paper,we discussed the property of rectangular band semiring congruence and ring congruence on a semiring and gave some characterizations and structure of rectangular ring congruence on an E-inversive semiring.
congruence;band semiring;E-inversive semiring
§1.Introduction and Preliminaries
A semiring S is def i ned as an algebra system(S,+,·)consisting of a nonempty set S together with two binary operations+and·such that(S,+)and(S,·)are semigroups connected by a·(b+c)=a·b+a·c,(a+b)·c=a·c+b·c,for any a,b,c∈S.Usually,we write(S,+,·) simply as S and for any a,b∈S,we write a·b simply as ab.
A subsemiring A of a semiring S is called an ideal of S if sa,as∈A for all a∈A,s∈S. We denote E+(S)the set of all additive idempotents of S.It is easy to see that(E+(S),·)is an ideal of(S,·).
A semiring S is a skew-ring if its additive reduct(S,+)is a group.A semiring S is an idempotent semiring if it satisf i es a+a=a·a=a for all a∈S(that is,both the reducts(S,+) and(S,·)are bands).A band semiring is an idempotent semiring S satisfying the following conditions

530CHINESE QUARTERLY JOURNAL OF MATHEMATICSVol.29 for any a,b∈S[4].A T band semiring S is a band semiring such that the additive reduct (S,+)of S is a T band[4].In[10],the authors proved that band semirings are always regular band semirings.
Semirings and band semirings with special reduct are studied in[1,9-10,12-13].In[5-8], some properties of E-inversive semigroup are studied.GIGON R S discussed the property of group congruence[2]and give some characterizations and structure of rectangular group congruence[3]on an E-inversive semigroup.
In this paper,we will obtain some results about rectangular band semiring congruences and ring congruences on a semiring,and give some characterizations and structure of rectangular ring congruences on an E-inversive semiring.
Throughout this paper we shall use the terminology and notations of[1,5].Firstly,we list some results we shall use in the following.
Theorem 1.1[9]A rectangular band semiring is isomorphic to the direct product of a left zero band semiring and a right zero band semiring.
Lemma 1.2[5]The following statements about a semigroup S are equivalent
(1)S is a rectangular band;
(2)(∀a,b∈S)ab=ba=⇒a=b;
(3)(∀a,b∈S)aba=a;
(4)(∀a,b,c∈S)a·a=a,abc=ac.
A semiring S is called an E-inversive semiring if there exists x∈S such that a+x∈E+(S) for any a∈S.Let S be a semiring and a∈S.An element x is called a weak inverse of a if x=x+a+x.Denote the set of all weak inverses of a in S by W(a)={x∈S:x=x+a+x}.
Proposition 1.3A semiring S is an E-inversive semiring if and only if W(a)is nonempty for all a∈S.
ProofLet S be an E-inversive semiring.For any a∈S,there exists x∈S such that a+x∈E+(S).Let y=x+a+x.Then

therefore,y∈W(a).Hence W(a)is nonempty.
Conversely,if W(a)is nonempty for all a∈S,then x=x+a+x for some x∈S,therefore, a+x=a+x+a+x.So a+x∈E+(S)for all a∈S,we deduce that S is an E-inversive semiring.
By the above proposition,easily,if S is an E-inversive semiring,then there is x∈S such that a+x,x+a∈E+(S)for any a∈S.
Let C be a class of semiring.We say that a congruence ρ on a semiring S is a C-congruence if S/ρ∈C.For example,if C is the class of rings,then ρ is called a ring congruence on S ifS/ρ is a ring.In this way,we can def i ne rectangular band semiring congruence and rectangular ring congruence on a semiring S similarly.
Let ρ be a congruence on a semiring S.The kernel kerρ of ρ is the set{x∈S:(∃e∈E+(S))xρe}.The trace trρ is the restriction of ρ on E+(S).
Easily,based on the above def i nitions and results,we can get the following characterizations about rectangular ring congruences and ring congruences.
Proposition 1.4Let S be an E-inversive semiring and ρ a rectangular band semiring congruence.Then every ρ-class of S contains an idempotent of S and kerρ=S.Also,each rectangular band semiring congruence on S is uniquely determined by its trace.
Proposition 1.5Let ρ be a ring congruence on a semiring S.Then trρ is the trivial relation on E+(S).Also,each ring congruence on S is uniquely determined by its kernel.
§2.Rectangular Ring Congruence
Def i nition 2.1[13]A semiring S is called a rectangular ring if and only if S is isomorphic to the direct product M×R of a rectangular band semiring M and a ring R.
Every rectangular band semiring and every ring is a rectangular ring,so every rectangular band semiring congruence and every ring congruence on a semiring S is a rectangular ring congruence on S.Clearly,the intersection of a rectangular band semiring congruence and ring congruence on S is a rectangular ring congruence on S.Conversely,the following theorem implies that each rectangular ring congruence on an E-inversive semiring can be expressed in this way,and this expression is unique.
Let A be a nonempty subset of a semiring S.Then A is called quasi dense,if it satisf i es the following two conditions that for any a,b∈S
(1)a∈A⇐⇒a+a∈A;
(2)a+b∈A⇐⇒a+S+b⊆A.
Let S be a semigroup.Then S is called an inversive semigroup,if it satisf i es the following two conditions
(1)S has an idempotent,and the set of idempotents E(S)is a subband of S;
(2)For any element x of S,there exists an element x∗such that xx∗=x∗x and xx∗x=x[11].
Let ρ be a rectangular ring congruence on a semiring S,ρ be the canonical epimorphism from S onto S/ρ.That is,S/ρ=M×R,where M is a rectangular band semiring and R is a ring. For any m∈M,we denote Qm={a∈S:aρ∈{m}×R}and N={a∈S:aρ∈E+(M×R)}.
Proposition 2.2Let ρ be a rectangular ring congruence on a semiring S,Qmbe def i ned as above.Then Qmis a quasi dense and E-inversive semiring,S=∪{Qm:m∈M}.
ProofLet ρ be a rectangular ring congruence on a semiring S.Then S/ρ=M×R,where M is a rectangular band semiring,R is a ring.
Clearly,Qmis a nonempty subset of S.For any a,b∈Qm,there is r1,r2∈R such that aρ=(m,r1),bρ=(m,r2),therefore
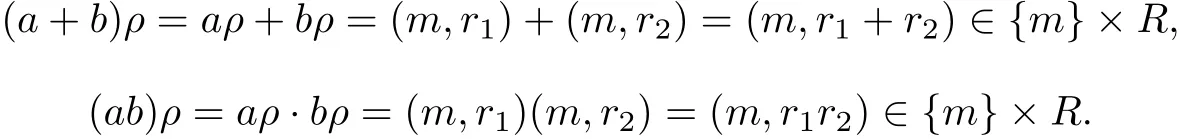
It follows that a+b,ab∈Qm.Now,we deduce that Qmis a subsemiring of S.Let a∈Qm. There is r∈R such that aρ=(m,r),therefore
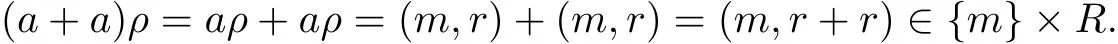
It follows that a+a∈Qm.Let a∈S and a+a∈Qm.There is r∈R such that(a+a)ρ=(m,r). If aρ=(n,r1),where n∈M,r1∈R,then
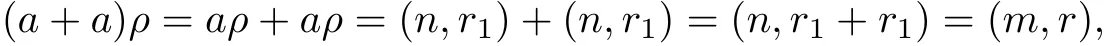
so that m=n.It follows that aρ=(m,r1)∈{m}×R.Hence a∈Qm.Let a,b∈S be such that a+b∈Qm.Then(a+b)ρ=(m,r)for some r∈R.If aρ=(m1,r1),bρ=(m2,r2)where m1,m2∈M,r1,r2∈R,then
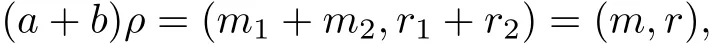
so that m1+m2=m.For any c∈S,then cρ=(m3,r3)for some m3∈M,r3∈R,
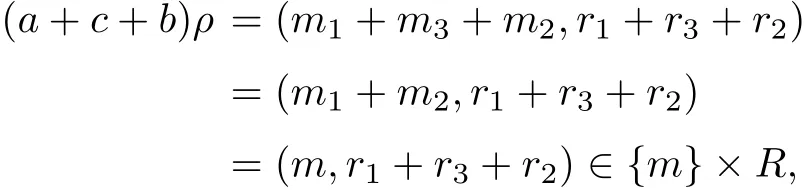
since M is a rectangular band semiring,so a+c+b∈Qm.Similarly,if a+c+b∈Qm,we can prove that a+b∈Qm.Hence Qmis a quasi dense subsemiring of S.Since Qmis an inversive semigroup,we have Qmis an E-inversive semiring clearly.
Finally,we show that S=∪{Qm:m∈M}.It is easy to see that the union is disjoint and for all m∈M,Qm⊆S,so∪{Qm:m∈M}⊆S.Conversely,let a∈S.There is m∈M,r∈R such that aρ=(m,r)since ρ is an epimorphism,so a∈Qm⊆∪{Qm:m∈M}.Consequently, S=∪{Qm:m∈M}.
Let A be a nonempty subset of a semiring S.If A contains all the additive idempotents of S,then A is called full.If a+b∈A implies b+a∈A for any a,b∈S,then A is called ref l exive.If for any s∈S,there exist x,y∈S such that s+x,y+s∈A,then A is called dense.Again,we denote the closure operator w on S by Aw={s∈S:(∃a∈A)a+s∈A}.If Aw=A,then A is called closed.A subsemiring N of a semiring S is normal if and only if N is full,dense,ref l exive,closed and an ideal of S.
Note that if S is an E-inversive semiring,then E+(S)is dense.Hence,every full subsemiring of E-inversive semiring S is dense.Further,a subsemiring A of an E-inversive semiring S is normal if and only if A is full,ref l exive,closed and an ideal of S.
Proposition 2.3Let ρ be a rectangular ring congruence on a semiring S.N,Qmbe def i ned as above.Then for all m∈M,N∩Qmis a normal subsemiring of Qm.
ProofLet m∈M.Put Nm=N∩Qm.For any a,b∈Nm,then aρ=bρ=(m,0). Easily,we can prove that a+b,ab∈Nm,so Nmis a subsemiring of Qm.For any e∈E+(Qm), then eρ=(m,0)∈M×{0R}which imples e∈Nm.That is,Nmis full.Let a,b∈Qmbe such that a+b∈Nm.Suppose that aρ=(m,r1),bρ=(m,r2)where m∈M,r1,r2∈R.Then
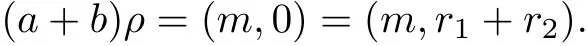
It follows that r1+r2=0.Because R is a ring,we obtain that
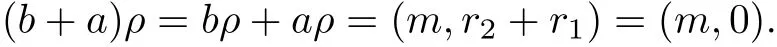
Now,we have b+a∈Nmand so Nmis ref l exive.If a∈Qm,there is r∈R such that aρ=(m,r). Let a′∈Qmand a′ρ=(m,−r),where−r is an additive inverse of r.Then
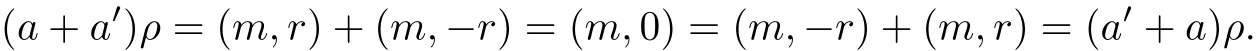
Hence a+a′,a′+a∈Nm,which implies Nmis dense.Let a∈Nmw.There exists b∈Nmsuch that b+a∈Nm.Moreover(a+b)ρ=(b+a)ρ=(m,0),so
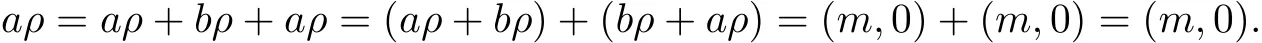
It follows that a∈Nm.It is easy to see that Nm⊆Nmw.Hence Nmis closed.Let a∈Nmand b∈Qmbe such that aρ=(m,0)and bρ=(m,r),where m∈M,r∈R.Then
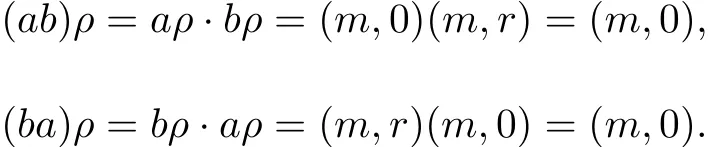
It follows that ab,ba∈Nm.Now,we have Nmis an ideal of Qm.Consequently,N∩Qmis a normal subsemiring of Qm.
Proposition 2.4Let ρ be a rectangular ring congruence on a semiring S.Then the relation v={(a,b)∈S×S:(∃m∈M)a,b∈Qm}is a rectangular band semiring congruence on S.
ProofBy Proposition 2.2,we have S=∪{Qm:m∈M}and Qmis a quasi dense subsemiring of S.Firstly,we shall show that v is a congruence on S.Clearly,v is an equivalence relation on S.Let(a,b)∈v.There exists m∈M such that a,b∈Qm,so aρ=(m,r1),bρ= (m,r2)for some r1,r2∈R.For any c∈S,then cρ=(n,r)for some n∈M,r∈R.Further,
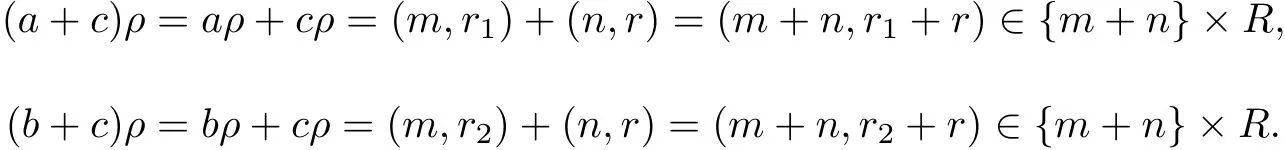
Thus a+c,b+c∈Qm+n,so(a+c,b+c)∈v.Similarly,we can prove that(c+a,c+b)∈v,(ac,bc)∈v,(ca,cb)∈v.Hence v is a congruence on S.
Finally,we shall show that S/v is a rectangular band semiring.Let a∈S.There exists m∈M such that a∈Qm.Since Qmis a subsemiring of S,we have a+a,a·a∈Qm,so (a,a+a)∈v,(a,a·a)∈v and then av=av+av=av·av.For any a,b,c∈S,then a+b+c∈Qmfor some m∈M.a+c∈Qmbecause of Qmis a quasi dense.Further, (a+b+c,a+c)∈v,so av+bv+cv=av+cv.Now,we know that S/v is a rectangular band semiring.Hence v is a rectangular band semiring congruence on S.
Proposition 2.5Let S be an E-inversive semiring and N be a normal subsemiring of S. Then the relation ρN={(a,b)∈S×S:(∃x,y∈N)x+a=b+y}is a skew-ring congruence on S and kerρN=N.
ProofFirstly,we show that ρNis a congruence on S.Let a,b,c∈S.Suppose that a′∈W(a)since S is an E-inversive semiring,W(a)is nonempty.By N is full,then a′+a,a+a′∈E+(S)⊆N.Note that(a+a′)+a=a+(a′+a),we have(a,a)∈ρN. Suppose that(a,b)∈ρN.Then x+a=b+y for some x,y∈N.If a′∈W(a),b′∈W(b), then a+a′+x∈N,y+b′+b∈N.It follows that a′+x+a∈N,b+y+b′∈N since N is ref l exive,so a′+x+a+b′+b∈N,a+a′+b+y+b′∈N.Further,

Hence(b,a)∈ρN.Suppose that(a,b)∈ρN,(b,c)∈ρN.Then x+a=b+y,z+b=c+w for some x,y,z,w∈N.Thus(z+x)+a=z+b+y=c+(w+y)and z+x,w+y∈N, it follows that(a,c)∈ρN.Hence ρNis an equivalence relation on S.Suppose that(a,b)∈ρNand c∈S.Then x+a=b+y for some x,y∈N.If b′∈W(b),c′∈W(c),then
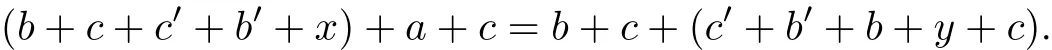
Since b+c+c′+b′+x,c′+b′+b+y+c∈N,we have(a+c,b+c)∈ρN.Hence ρNis an additive right compatible.Dual,we can show that ρNis an additive left compatible.Suppose that(a,b)∈ρNand c∈S.Then x+a=b+y for some x,y∈N,therefore,
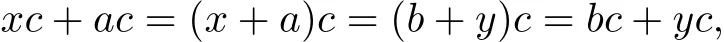
where xc,yc∈N since N is an ideal of S.We deduce that(ac,bc)∈ρN.Dual,we can prove that(ca,cb)∈ρN.Hence ρNis a congruence on S.
Next,we shall show that ρNis a skew-ring congruence on S.Clearly,S/ρNis a semiring, we just need to prove that(S/ρN,+)is a group.For any x∈N.Claim that xρNis the identity of S/ρN.Let a∈S and a′∈W(a).Then a+x+a′,a′+a∈N and
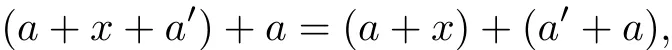
that is,(a,a+x)∈ρN.Note that x+a+a′,a′+a∈N and

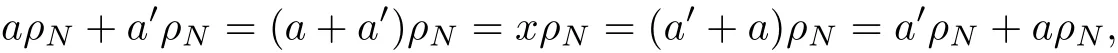
so(a,x+a)∈ρN.We obtain that xρNis the identity of S/ρN.Clearly,xρN=yρN=eρNfor all x,y∈N,e∈E+(S).Thenit follows that a′ρNis an inverse of aρN.Now,we have S/ρNis a group.Consequently,ρNis a skew-ring congruence on S.
Finally,we shall show that kerρN=N.Let a∈N and a′∈W(a).Then
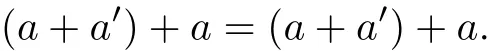
Since a+a′∈E+(S)⊆N,we deduce that(a,a+a′)∈ρN,so a∈kerρN.Let a∈kerρN. There is e∈E+(S)such that(a,e)∈ρN,therefore,x+a=e+y for some x,y∈N.Since e,y∈N,we have e+y∈N and so x+a∈N.We have a∈N since N is closed.Consequently, kerρN=N.
From the above proposition we obtain the following corollary.
Corollary 2.6Let S be an E-inversive semiring and N be a normal subsemiring of S. Then(a,b)∈ρNif and only if a+x,b+x∈N for some x∈S.
Now,we give a characterization of rectangular ring congruences on an E-inversive semiring.
Theorem 2.7Let S be an E-inversive semiring and ρ be a rectangular ring congruence on S.Then ρ=v∩ρNwhere v and N are def i ned as above,and it is unique of this expression.
ProofNotice that N is the preimage of M×{0R}by the canonical epimorphism ρ . We f i rst show that N is a normal subsemiring of S.Clearly,N is a nonempty subset of S.If a,b∈N,then aρ=(m,0),bρ=(n,0)for some m,n∈M.It follows that
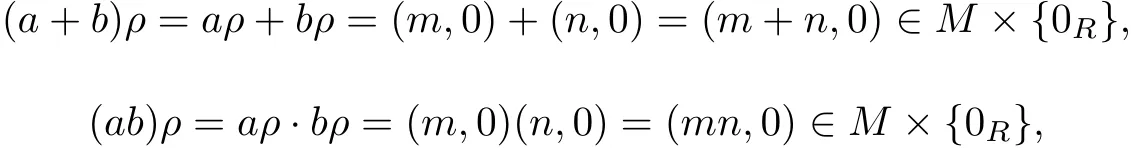
so a+b,ab∈N.We have N is a subsemiring of S.For any a∈N and x∈S,then aρ=(m,0),xρ=(n,r)for some m,n∈M,r∈R.It follows that
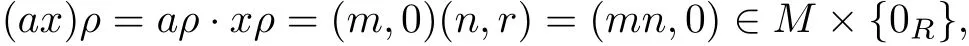
so ax∈N,we deduce that NS⊆N.Dual,we have SN⊆N.Hence N is an ideal of S.For any e∈E+(S),then eρ∈E+(M×R),so e∈N.We deduce that N is full.Let a,b∈S be such that a+b∈N.Then(a+b)ρ=(m,0)for some m∈M.Let aρ=(m1,r1),bρ=(m2,r2) for some m1,m2∈M,r1,r2∈R.Then m1+m2=m,r1+r2=0.Further,


since R is a ring.Hence b+a∈N which implies N is ref l exive.Let a∈Nw.There exists b∈N such that b+a∈N.Let aρ=(m,r),bρ=(n,0)for some m,n∈M,r∈R.Thenit follows that r=0.Further,aρ=(m,0)∈M×{0R}.Hence a∈N and Nw⊆N.Conversely, let a∈N.For any b∈N,then b+a∈N since N is a subsemiring of S.Hence a∈Nw and N⊆Nw.We obtain that N is closed.Consequently,N is a normal subsemiring of S.
Secondly,by Proposition 2.5,we know that ρNis a skew-ring congruence on S.For any a,b∈S,then aρ=(m1,r1),bρ=(m2,r2),where m1,m2∈M,r1,r2∈R.Let x∈S and xρ=(m,−r1−r2),where m∈M,−r1,−r2are ring additive inverses of r1,r2in S, respectively.Then
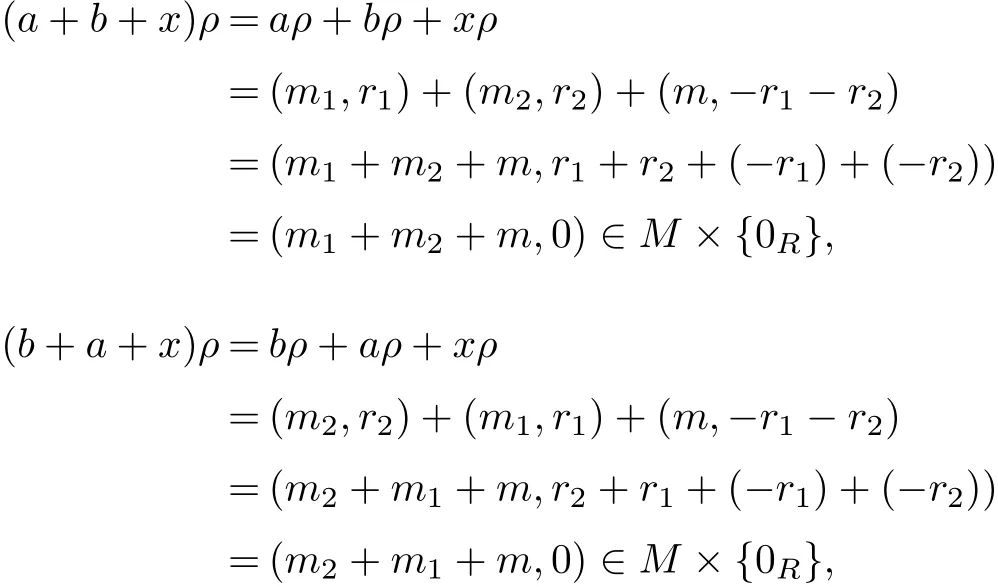
since R is a ring.So a+b+x,b+a+x∈N,(a+b,b+a)∈ρNby Corollary 2.6.We have (S/ρN,+,·)is a ring and ρNis a ring congruence on S.By Proposition 2.4,we know that v is a rectangular band semiring congruence on S.
Thirdly,we shall show that ρ=v∩ρN.Let(a,b)∈ρ and aρ=(m,r)where m∈M,r∈R. Let x∈S be such that xρ=(m,−r)where−r is a ring additive inverse of r in R.Then
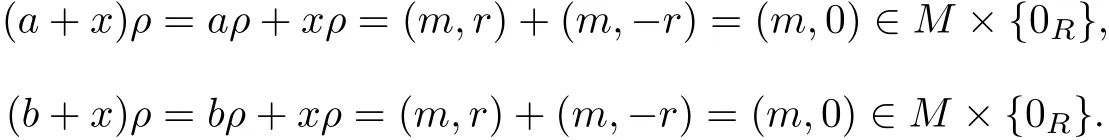
It follows that a+x,b+x∈N,so(a,b)∈ρN.Also,aρ=(m,r)=bρ∈{m}×R.Hence a,b∈Qmand(a,b)∈v.We obtain that(a,b)∈v∩ρN.Consequently,ρ⊆v∩ρN.Conversely, let(a,b)∈v∩ρN.Then aρ,bρ∈{m}×R(aρ=(m,r1),bρ=(m,r2)),a+x,b+x∈N for some m∈M,x∈Qn,where n∈M.Let xρ=(n,r).Then
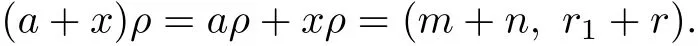
On the other hand(a+x)ρ∈M×{0R},hence r1=−r.Similarly,we can prove that r2=−r. Thus(a,b)∈ρ.Consequently,ρ=v∩ρN.
Finally,we shall show that this expression is unique.Suppose that ρ=v∩ρN=v∗∩ρ∗N. Let(a,b)∈v.Because v∩v∗is a rectangular band semiring congruence,we know that there exists e,f∈E+(S)such that e∈a(v∩v∗),f∈b(v∩v∗)by Proposition 1.4,so (a,e)∈v∩v∗⊆v,(f,b)∈v∩v∗⊆v and(e,f)∈v.Since ρNis a ring congruence,we have (e,f)∈trρN⊆ρNby Proposition 1.5.Therefore,(e,f)∈v∩ρN=v∗∩ρ∗N⊆v∗.Further, (a,e)∈v∗,(e,f)∈v∗,(f,b)∈v∗,thus(a,b)∈v∗.Hence v⊆v∗.We may equally well show the opposite inclusion.
Then v∗=v,so ρ=v∩ρN=v∩ρ∗N.Let(a,b)∈ρN.Since(a+a+b,a+b)∈v and (a+b+b,a+b)∈v,we have(a+a+b,a+b+b)∈v,so

Since S is an E-inversive semiring,we know that there exists a′∈W(a)and b′∈W(b)such that a′+a,b+b′∈E+(S).By(a+a+b,a+b+b)∈ρ∗N,then
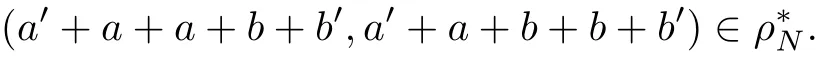
By Proposition 2.5,we know that(a′+a)ρ∗N=(b+b′)ρ∗Nis the identity of S/ρ∗N.Therefore, (a′+a+a+b+b′,a)∈ρ∗Nand(b,a′+a+b+b+b′)∈ρ∗N,so(a,b)∈ρ∗N.We deduce that ρN⊆ρ∗N.Similarly,we have ρ∗N⊆ρN.Thus ρN=ρ∗Nand the conclusion holds.
From Proposition 1.4,Proposition 1.5 and Theorem 2.7,we obtain the following two corollaries.
Corollary 2.8Let ρ be a rectangular ring congruence on an E-inversive semiring S. Then S/ρ~=S/v×S/ρN.
Corollary 2.9Let S be an E-inversive semiring.Then each rectangular ring congruence on S is uniquely determined by its kernel and trace.
Theorem 2.10Let ρ be a rectangular ring congruence on an E-inversive semiring S. Then for any m∈M,S/ρN~=Qm/ρ(N∩Qm).
ProofLet m∈M.Put Nm=N∩Qm.Def i ne the mapping φ:Qm/ρNm→S/ρNby (aρNm)φ=aρN(a∈Qm).By Proposition 2.5,we have ρNmis a congruence on Qm.Clearly,φ is well-def i ned.Further,let a∈S and c∈Nm⊆N.Then aρ=(n,r)and cρ=(m,0),where m,n∈M,r∈R.It follows that
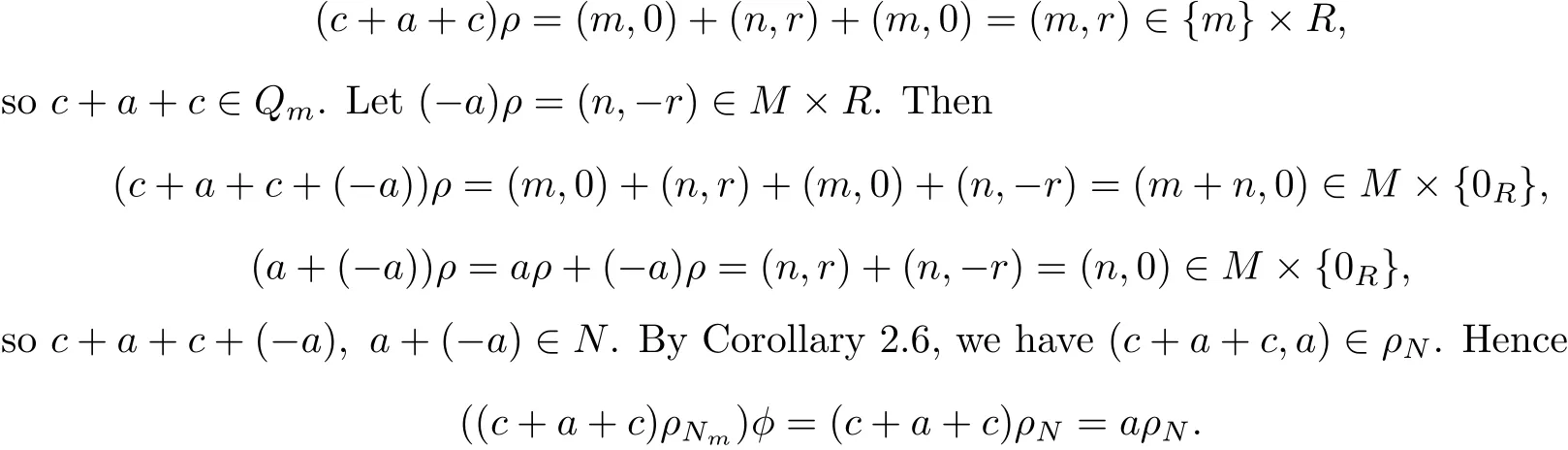
We know that φ is surjective.Let a,b∈Qmand(aρNm)φ=(bρNm)φ.Then(a,b)∈ρN,so a+x,b+x∈N for some x∈S.Moveover,for every c∈Nm⊆N,a+c+x,b+c+x∈N since N is ref l exive.Thus
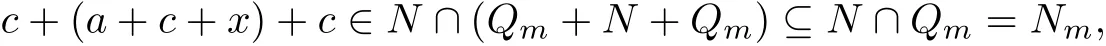
since(Qm+N+Qm)⊆Qmand similarly,we have c+(b+c+x)+c∈Nm.Since c+ a,c+b,c+x+c∈Qm,we deduce that(c+a,c+b)∈ρNm.By Proposition 2.5,we have c∈Nm=kerρNm,there exists e∈E+(Qm)such that cρNm=eρNm.So
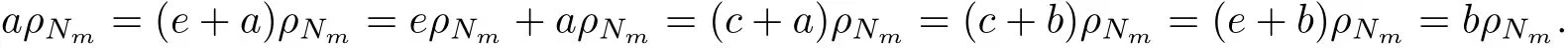
We know that φ is injective.For any a,b∈Qm,
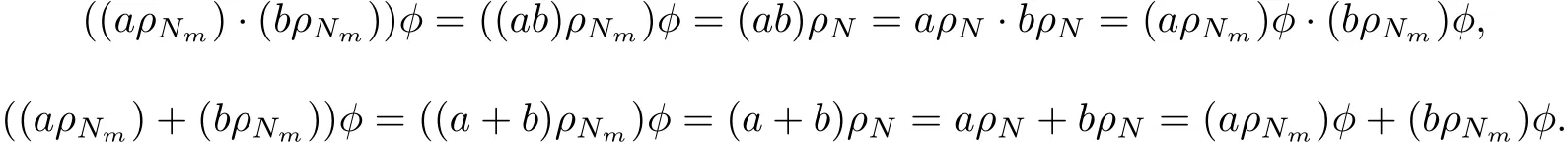
Hence S/ρN~=Qm/ρ(N∩Qm).
[1]GOLAN J S.The Theory of Semirings and Their Applications[M].The Netherlands:Kluwer Academic Publisher,1999.
[2]GIGON R S.Congruences and group congruences on a semigroup[J].Semigroup Forum,2013,86(2):431-450.
[3]GIGON R S.Rectangular group congruences on a semigroup[J].Semigroup Forum,2013,86(2)451-459.
[4]GUO Yu-qi,SHUM K P,SEN M K.The semigroup structure of left clif f ord semigroups[J].Acta Math Sin, 2003,19(4):783-792.
[5]HOWIE J M.An Introduction to Semigroup Theory[M].London:Acadmic Press,1976.
[6]PETRICH M.Inverse Semigroups[M].New York:Wiley,1983:1-674.
[7]SIRIPITUKDET M,SATTAYAPORN S.Band congruences on E-inversive E-semigroups[J].International Journal of Algebra,2010,4(19):923-929.
[8]SIRIPITUKDET M,SATTAYAPORN S.The least group congruence on E-inversive semigroups and E-inversive E-semigroups[J].Thai Journal of Mathematics,2005,3(2):163-169.
[9]SEN M K,GUO Yu-qi,SHUM K P.A class of idempotent semiring[J].Semigroup Forum,2000,60:351-367.
[10]WANG Zheng-pan,ZHOU Yuan-lan,GUO Yu-qi.A note on band semirings[J].Semigroup Forum,2005, 71:439-442.
[11]YAMADA M.Inversive semigroups I[J].Proc Japan Acad,1963,39:100-103.
[12]ZHOU Yuan-lan.Orthodox semiring with additive idempotents satisfy permutation identities[J].Journal of Mathematical Research and Exposition,2006,26(4):715-719.
[13]ZHOU Yuan-lan,GUO Yu-qi,WANG Zheng-pan.The semigroup structure of orthorings[J].Acta Math Sci, 2008,28(6):1097-1102.
tion:20M10,16Y60
1002–0462(2014)04–0529–10
date:2013-01-23
Supported by the National Natural Science Foundation of China(10961014,11101354); Supported by the Natural Science Foundation of Jiangxi Province(0611051);Supported by the Science Foundation of the Education Department of Jiangxi Province(GJJ09459)
Biography:CHENG Zi-qiang(1988-),male,native of Shangrao,Jiangxi,a master of Jiangxi Normal University,M.S.D.,engages in algebraic theory of semigroups.
CLC number:O152.7Document code:A
 Chinese Quarterly Journal of Mathematics2014年4期
Chinese Quarterly Journal of Mathematics2014年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- On the Cycle Structure of Iteration Graphs over the Unit Group
- On the Strong Rates of Convergence for Arrays of Rowwise Extended NegativelyDependent Random Variables
- Some Notes on G-cone Metric Spaces
- On Laguerre Isopararmetric Hypersurfaces in ℝ7
- On a Discrete Fractional Boundary Value Problem with Nonlocal Fractional Boundary Conditions
- Fast Parallel Method for Polynomial Evaluation at Points in Arithmetic Progression
