Study on the Relation of Def i nite Integral and Indef i nite Integral

SUN Bao-fa

(Department of Computer Science and Technology,Anhui Sanlian University,Hefei 230601,China)

Study on the Relation of Def i nite Integral and Indef i nite Integral

SUN Bao-fa

(Department of Computer Science and Technology,Anhui Sanlian University,Hefei 230601,China)

Relation of def i nite integral and indef i nite integral was discussed and an important result was gotten.If f(x)is bounded and has primary function,the formal def i nite integralxs˜f(t)dt is the indef i nite integral of f(x),where x is a self-variable,s is a parameter,˜f(x)is a function def i ned in(−∞,+∞),which comes from f(x)by restriction and extension.In other words,the indef i nite integral is a special form of def i nite integral,its lower integral limit and upper integral limit are all indef i nite.

def i nite integral;indef i nite integral;primary function

§1.Introduction

The English word integral means whole according to etymology.We can get a whole object by piecing together the microscopic pieces,which are cut down from the object.Therefore,the word integral has the meaning of accumulating microscopic elements.

Calculating ofbaf(x)dx is a process of cutting and accumulating the microscopic elements of an object on a def i nite interval[a,b].The English phase def i nite integral just announces the essence of the calculating process.

However,calculating off(x)dx is a process to f i nd any primary function of f(x),it doesn’t concern cutting the whole object,nor accumulating microscopic elements.Why is it named as integral?So it seems not precise to call the process as indef i nite integral.

In this paper the problem is discussed in detail,and the relation of de fi nite integral and inde fi nite integral was discussed deeply.The conclusion is that it is reasonable to namef(x)dx as inde fi nite integral in some sense.

§2.Def i nition Analyses of Def i nite Integral and Indef i nite Integral

2.1The Essence of the Def i nite Integral Def i nition

Consider calculating the area S of a curvilinear trapezoid{(x,y)|a≤x≤b,0≤y≤f(x)} by dif f erential method[1].The calculating process includes four steps:cutting,approximately replacing,summing and seeking limit,among which there are two essential steps.

(1)Cutting microscopically.Cut[a,b]to unnumbered tiny intervals,sort out a typical interval[x,x+dx]and get a tiny curvilinear trapezoid on[x,x+dx]accordingly.

(2)Summing totally.Accumulate the unnumbered tiny areas of tiny curvilinear trapezoids on[a,b]and gain S=baf(x)dx.

On the fi rst step,we microscopically cut S to unnumbered parts ΔS atisfying ΔS≈dS, and get di ff erential section dS of S.On this step,we are di ff erentiating S actually.On the second step,we sum these di ff erential areas ΔS,i.e.,accumulate dS on[a,b]and gaindS=f(x)dx.In fact,this step is integration,accumulating microscopic elements.

By this specif i c example,we can f i nd out that the dif f erential method includes two steps, dif f erentiation and integration,and this method is the unity of the two steps.It is just the unity of the two steps that announces the essence of dif f erential and integral calculus.

2.2The Weakness of the Indef i nite Integral Def i nition

(1)The weakness of the def i nition off(x)dx.

The indef i nite integral of f(x),f(x)dx,represents any primary function of f(x),i.e.,it is a representative of all primary functions of f(x).In the process of calculatingf(x)dx,we don’t dif f erentiate anything,nor accumulate any microscopic elements.From this point,f(x)dx isn’t an integral.Hence,it is not precise to namef(x)dx as indef i nite integral.

(2)The weakness of the def i nition o

The formal def i nite integral with f i xed lower limit of integral and variable upper limit of integral Φ(x)=xaf(t)dt(x∈[a,b])is a primary function of f(x)on[a,b]if f(x)∈C[a,b]. It can be known in the course of Mathematical Analysis[1].However,this formula doesn’t give full expression to integral constant c,soxaf(t)dt is not the indef i nite integral of f(x).

In the course of Function of Real Variable[2],the indef i nite integral is def i ned as following. Let f∈L(A),F(E)=Ef(y)dy is called as the indef i nite integral of f,where E is any measurable subset of A.i.e.,indef i nite integral is integral on indef i nite measurable set.Applythis def i nition to f(x)(f(x)∈C[a,b]),select any point s∈[a,b],then

In short,it is not precise to namef(t)dt orf(y)dy as inde fi nite integral.

§3.The Indef i nite Integral Def i ned by Def i nite Integral 3.1For the Continuous Function on a Finite Closed Interval

At f i rst,we assume that f(x)≥0(x∈[a,b]).

Extend f(x)continuously and get˜f(x)in(−∞,+∞),meeting the conditions˜f(x)=

Let the lower limit of integral vary to s,the upper limit of integral vary to x and obtain a formal def i nite integralxs˜f(t)dt(s∈(−∞,+∞),x∈(−∞,+∞))with variable lower limit of integral and upper limit of integral,then we gain

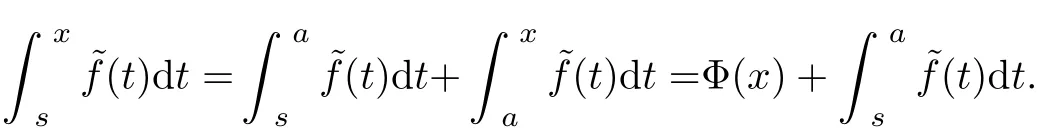
The formal def i nite integral with variable upper limit of integral Φ(x)=xa˜f(t)dt(x∈[a,b]) is a primary function of f(x)on[a,b].According to the conditions of˜f(x),as˜f(t)dt is a continuous function of s.Since=+∞and,there is a certain s′∈(−∞,+∞)atisfying=c for any constant c.Therefore,we conclude that, let variable upper limit of integral x be a self-variable,variable lower limit of integral s be a parameter,the formal def i nite integralxs˜f(t)dt is the indef i nite integral of f(x)on[a,b].

If f(x)≤0(x∈[a,b]),or f(x)is neither non-negative nor non-positive,we can discuss it similarly and get the same conclusion.

3.2For the Continuous Function in a Inf i nite Open Interval

For f(x)∈C(−∞,+∞),e.g.,f(x)=sinx,though

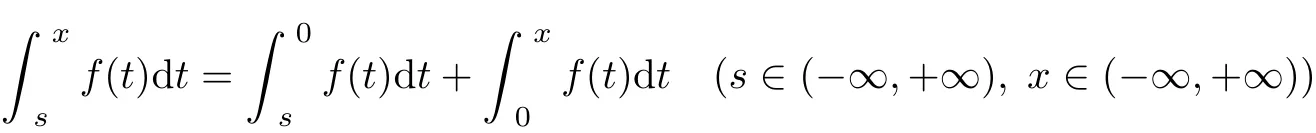
is a primary function of f(x)in(−∞,+∞),there is no parameter s satisfyingasf(t)dt=c, say,c=10.Thus,xsf(t)dt isn’t the indef i nite integral of f(x)in(−∞,+∞).

To solve this problem,we introduce the following concepts.

Def i nition 1Let f(x)be def i ned in interval I,F(x)is called as a primary function of f(x)at point x and F(x)+c is called as the indef i nite integral of f(x)at point x,if f there are a neighborhood U(x)of point x(x∈I)and a dif f erential function F(x),satisfying F′(x)=f(x)(x∈U(x)).

Def i nition 2f(x)has indef i nite integral in interval I,if ff(x)has indef i nite integral at any point x(x∈I).

Now we return to the preceding problem.For any point x(x∈(−∞,+∞)),construct a close interval[a,b],satisfying x∈(a,b).A function¯f(x)(x∈[a,b])is gotten by restricting the function f(x)from(−∞,+∞)to[a,b].Extend¯f(x)(x∈[a,b])continuously to(−∞,+∞) and get a function˜f(x)meeting the conditions˜f(x)=¯f(x)(x∈[a,b]),a−∞˜f(t)dt=+∞,a

+∞˜f(t)dt=−∞.It is clear that

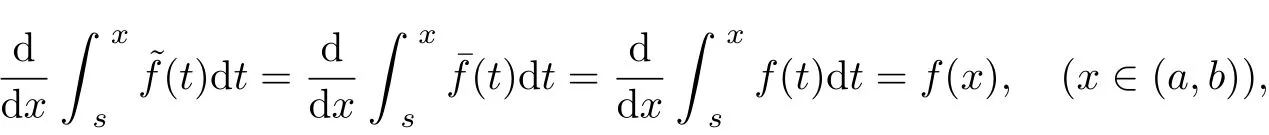
i.e.,xs˜f(t)dt is the indef i nite integral of f(x)at point x.

By this means,we can gain the indef i nite integral of f(x)in(−∞,+∞).

3.3For the Continuous Function on a Finite Closed Interval or Open Interval

Be similar to 3.2,for any point x(x∈(c,d)([c,d)or(c,d])),construct a close interval[a,b] satisfying x∈(a,b),[a,b]⊂(c,d)([c,d)or(c,d]).At f i rst,restrict the function f(x)to[a,b] and get a function¯f(x)(x∈[a,b]).Secondly,extend¯f(x)(x∈[a,b])to(−∞,+∞)and get a continuous function˜f(x).Then,xs˜f(t)dt is the indef i nite integral of f(x)at point x.

Similarly,we can obtain the indef i nite integral of f(x)in(c,d)([c,d)or(c,d]).

3.4For the Function Which Has Primary Function

We assumed f(x)be continuous in each interval concerned in 3.1,3.2 and 3.3.In fact, we can get the same conclusion if f(x)is bounded and has primary function in an interval concerned.As an example,we only study function def i ned on[a,b].In the case of function f(x)def i ned in intervals of other form,we can discuss them as we do in 3.2 and 3.3.

Lemma 1If f(x)is bounded and has primary function F(x)on[a,b],F(x)is absolutely continuous on[a,b].

We can prove Lemma 1 by applying Langrange’s theorem of mean to F(x)[2]and get Lemma 2 according to Lemma 1 and Theorem 5.13[2].

Lemma 2If f(x)is bounded and has primary function,xaf(t)dt is a primary function of f(x)on[a,b].

According to Lemma 2,we can obtain the indef i nite integralxs˜f(t)dt of f(x)on[a,b]by the method used in 3.1.

Summing up all preceding conclusions,we gain

Theorem 1If f(x)is bounded and has primary function in interval I,the formal de fi nite integralxf˜(t)dt is the inde fi nite integral of f(x)in interval I,where x is a self-variable,s is as˜ parameter,f(x)is a function de fi ned in(−∞,+∞)which comes from f(x)by restriction and extension,f˜(x)is continuous in(−∞,+∞)−I and for a∈I,f˜(t)dt=+∞,f˜(t)dt=−∞.

§4.Notes

(1)As mentioned in 3.1,xf˜(t)dt is the inde fi nite integral of f(x)on[a,b],where,the ˜s

integrand isf(x),replacing the original function f(x).Just for the same reason,in 3.2,for f(x)de fi ned in(−∞,+∞),we don’t takexf(t)dt to represent the inde fi nite integral of f(x)s˜x˜ directly,but restrict and extend f(x)to getf(x),then,to obtainsf(t)dt,the inde fi nite integral of f(x)at point x.By this way,we overcome the difficulty in 3.2 smoothly.

(2)In 3.3,we also restrict and extend f(x).We don’t extend f(x)directly.The cause is that some continuous functions de fi ned in(c,d)([c,d)or(c,d])can’t be extended to continuous functions in(−∞,+∞).For example,continuous function f(x)=x1(x∈(0,1))can’t be extended to continuous function in(−∞,+∞).

(3)The condition that f(x)is bounded on[a,b]can’t be omitted in 3.4.In fact,even though f(x)has a primary function on[a,b],it is uncertain that f(x)is bounded on[a,b][3].e.g., has a primary function F(x)on[−1,1]

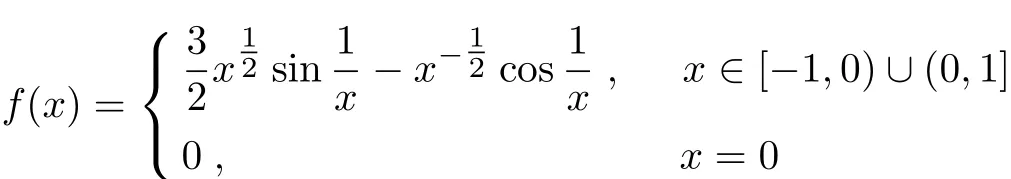
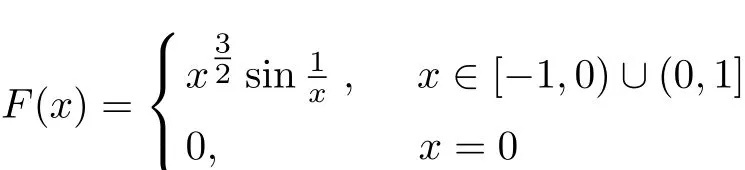
but f(x)is unbounded on[−1,1],furthermore,f(x)is unbounded on[−1,x](x∈(0,1]).Thus,f(t)dt is not de fi nite integral.As a result,xf(t)dt is not the inde fi nite integral of f(x)son[−1,1].

§5.Conclusion

The achievements of the paper is as follows.

(1)The unity of two sort integrals.The def i nition of indef i nite integral is given forcedly in current course of mathematical analysis.Neither does it explain whyf(x)dx=F(x)+c can be named as integral,nor does it account for the essence of indef i nite integral.This paper shows that def i nite integral is an integral whose lower integral limit and upper integral limitare all def i nite and that indef i nite integral is an integral whose lower integral limit and upper integral limit are all indef i nite.In other words,the indef i nite integral is a special form of def i nite integral.Therefore,it is reasonable to namef(x)dx as indef i nite integral.Thus,both integrals are similar in nature.This statement points out the relations of two sort integrals and the dif f erence between them clearly.

(2)Introduce of new concepts.In this paper three new concepts are given,such as primary function of f(x)at point x,indef i nite integral of f(x)at point x and indef i nite integral in interval I.As to the intention and the other application of these concepts,we shall discuss them in future.

tion:26A99

1002–0462(2014)04–0523–06

date:2013-01-02

Supported by the Colleges and Universities Provincial Scientif i c Research Project of Anhui Province(KJ2013B090)

Biography:SUN Bao-fa(1965-),male,native of Hefei,Anhui,an associate professor of Anhui Sanlian University,Ph.D.,engages in the qualitative theory of ordinary dif f erential equations,mathematical modeling and computer application.

CLC number:O172.2Document code:A

[1]CHENG Qi-xiang.Mathematical Analysis[M].Peking:Higher Education Press,1980:255-262,279-280.

[2]ZHOU Min-qiang.Functions of Real Variable[M].Peking:Peking University Press,1995:188-202.

[3]QIANG Wen-jiu,LI Yuan-zhang,HUANG Wen-rong.Basic Concepts and Methods of Mathematical Analysis[M].Peking:Higher Education Press,1989:103-143.