Linear Commuting Maps on Parabolic Subalgebras of Finite-dimensional Simple Lie Algebras

CHEN Zheng-xin,WANG Bing

(School of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350007,China)

Linear Commuting Maps on Parabolic Subalgebras of Finite-dimensional Simple Lie Algebras

CHEN Zheng-xin,WANG Bing

(School of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350007,China)

A map ϕ on a Lie algebra g is called to be commuting if[ϕ(x),x]=0 for all x∈g.Let L be a f i nite-dimensional simple Lie algebra over an algebraically closed f i eld F of characteristic 0,P a parabolic subalgebra of L.In this paper,we prove that a linear map ϕ on P is commuting if and only if ϕ is a scalar multiplication map on P.

commuting maps;f i nite-dimensional simple Lie algebras;standard parabolic subalgebras

§1.Introduction

Let A be an associative ring.A map ϕ:A→A is called commuting if

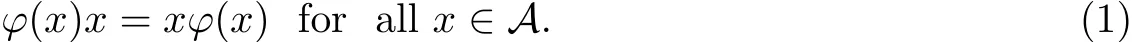
Let us denote the commutator or the Lie product of the elements x,y∈A by[x,y]=xy−yx. Accordingly(1)will be written as[ϕ(x),x]=0.The identity mapping and zero mapping are two classical examples of commuting maps.The principal task when treating a commuting map is to describe its form.Usually we consider commuting maps imposed with some restrictions, such as additive commuting maps,commuting traces,commuting automorphisms,commuting derivations,et al(see[1-2,4-5,8-9,11-16]).We encourage the reader to read the well-writtensurvey paper[3],in which the author presented the development of the theory of commuting mappings and their applications in details.

It is a natural question to def i ne and determine the commuting maps on Lie algebras.Let g be a Lie algebra with Lie product[−,−]over a f i eld F.A map ϕ:g→g is said to be commuting if[ϕ(x),x]=0 for all x∈g.Until now the authors have not found any result about commuting maps on simple Lie algebras or their subalgebras.This paper is dedicated to determine the linear commuting maps on any parabolic subalgebra of a f i nite-dimensional simple Lie algebra. As applications,we determine its commuting automorphisms and commuting derivations.

Recall some basic def i nitions and notations about f i nite-dimensional simple Lie algebras, which mainly follow from[10].Let F be an algebraically closed f i eld of characteristic 0.Let L be a f i nite-dimensional simple Lie algebra over F of rank l,η a f i xed standard Cartan subalgebra of L,Φ⊆η∗the corresponding root system,

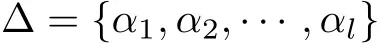
a f i xed base of Φ,Φ+(resp.,Φ−)the set of corresponding positive(resp.,negative)root system of L relative to Δ.For α∈Φ,let

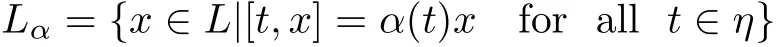
be the one-dimensional root space relative to α∈Φ.For each α∈Φ+,let eαbe a non-zero element of Lα,then there is a unique element e−α∈L−αsuch that eα,e−α,hα=[eα,e−α]span a three-dimensional simple subalgebra of L isomorphic to sl(2,F).The set{hα,eβ,e−β|α∈Δ,β∈Φ+}forms a basis of L.If α,β and α+β are roots,then[eα,eβ]is a scalar multiple of eα+β.We def i ne Nα,βby

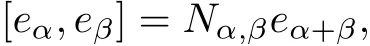
which we call the structure constants of L.We can choose a basis{hα,eβ,e−β|α∈Δ,β∈Φ+} of L such that all structure constants of L are integers,which we call a Chevalley basis of L.In the remainder of this paper,the set will always denote a Chevalley basis of L.Let

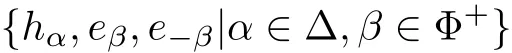
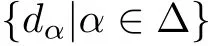
be the dual basis of η relative to Δ.Namely,β(dα)takes the value 0 when β/=α∈Δ, and takes the value 1 when β=α∈Δ.A symmetric bilinear form(−,−)is def i ned on the ldimensional real vector space spanned by Φ,which is dual to the Killing form k(−,−)on L.For α,β∈Φ,we say α is orthogonal to β,denoted by α⊥β,if(α,β)=0.Denote n+b=η+n+.b is usually called a standard Borel subalgebra of L.A subalgebra of L containing b is called a standard parabolic subalgebra.The conjugate of a standard parabolic subalgebra is called a parabolic subalgebra.From this point of view,if we determine the linear commuting maps on any standard parabolic subalgebra of a f i nite-dimensional simple Lie algebra,then wedetermine the linear commuting maps on any parabolic subalgebra.So the aim of this paper is to determine the linear commuting maps on standard parabolic subalgebras.

Let π be a subset of Δ and let Φπbe the set of the roots that are the Z-linear combinations of the elements in π.Set=Φ+∩Φπ.It is known that each standard parabolic subalgebra takes the form P= Fe−α,where π is a subset of Δ.In the follows,we will denote this one by

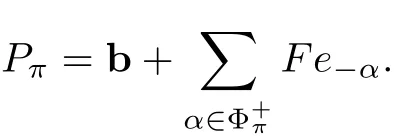
Note that Pπ=Feβ,where−Φ+π={−α|α∈Φ+π}.If π=∅,then Pπis the standard Borel subalgebra b;if π=Δ,then Pπis L itself.By calculation one will see that L has exactly 2lconjugacy classes of parabolic subalgebras,since distinct standard parabolic subalgebras cannot be conjugate.It is also known that Pπ1∩Pπ2=Pπ1∩π2,Pπ1+Pπ2=Pπ1∪π2for π1,π2⊆Δ.A subset π of Δ is called irreducible if it cannot be partitioned into the union of two proper subsets of π such that each simple root in one set is orthogonal to each simple root in the other.Otherwise,we say π is reducible.If π is reducible,then it has a partition into a number of irreducible components

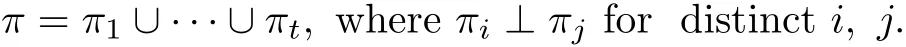
For any c∈F,def i ne a map

We call ϕca scalar multiplication map on Pπ.

The main result of this paper is as follows:

TheoremLet Pπbe a standard parabolic subalgebra of f i nite-dimensional simple Lie algebra over an algebraically closed f i eld F of characteristic 0.Then a linear map ϕ on Pπis a commuting map if and only if ϕ is a scalar multiplication map ϕλon Pπfor some λ∈F.

§2.Proof of the Main Results

The sufficient direction of the theorem is obvious.Now we prove the essential direction of the theorem.

Let ϕ be a commuting linear map on Pπ.For any x,y∈Pπ,[ϕ(x+y),x+y]=0,i.e.,

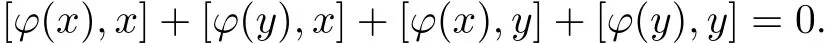
Since[ϕ(x),x]=[ϕ(y),y]=0,we have the equality

We will prove the main theorem in the following seven steps.

Step 1ϕ(η)⊆η.

By[6,Lemma 2.2],there exists h0∈η such that α(h0)/=β(h0)for any α/=β∈Φ∪{0}. Such an element h0in η is called strongly regular and CL(h0)=η,where

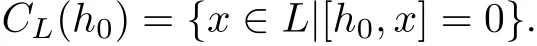
Moreover,since η⊆CPπ(h0)and CPπ(h0)⊆CL(h0)=η,then η=CPπ(h0).

By conditions,[ϕ(h0),h0]=0,and so ϕ(h0)∈CPπ(h0),which implies that ϕ(h0)∈η.

For any h∈η,[h0,ϕ(h)]=[ϕ(h0),h]=0 by the equality(2).Thus ϕ(h)∈CPπ(h0)=η. Therefore,ϕ(η)⊆η.

Step 2For any α∈Φ+∪{−Φ+π},there is an element tα∈η such that ϕ(eα)−tα∈Lα.

Given a f i xed α∈Φ+∪{−Φ+π},we denote

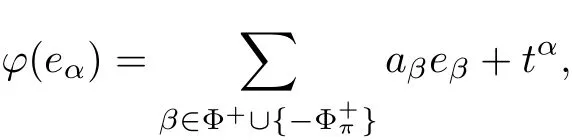
where tα∈η,aβ∈F for any β∈Φ+∪{−Φ+π}.By the equality

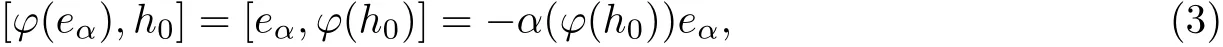
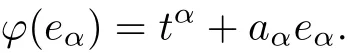
Therefore ϕ(eα)−tα=aαeα∈Lα.

Step 3For any i=1,2,···,l,there is a f i xed element λ∈F such that ϕ(eαi)=λeαi.

Given a i∈{1,2,···,l},ϕ(eαi)=aαieαi+tαiby Step 2.For any k=1,2,···,l,we have the equality

Comparing the coefficients of eαkon the both sides of the above equality(4),we have αk(tαi)=0.Since{dαi|i=1,2,···,l}is a basis of η,we can set∈F.By the de fi nition of dγ,we have β(dγ)=0 for β/=γ,and β(dβ)=1.Then αk(tαi)=,where=0 for any k=1,2,···,l.Thus=0.It follows that ϕ(eαi)=aαieαi∈Lαifor any i=1,2,···,l.

For a f i xed i∈{1,2,···,l},there is some j∈{1,2,···,l}such that αi+αj∈Φ+.By the equality

we have[aαieαi,eαj]=[eαi,aαjeαj],i.e.,aαi[eαi,eαj]=aαj[eαi,eαj].Since[eαi,eαj]= Nαi,αjeαi+αj/=0,we have aαi=aαj.By the connectedness of the Dynkin diagram of Δ, we haveNow we denote the same element by λ.Then Step 3 follows.

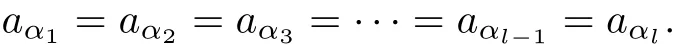
Step 4For any α∈Φ+∪{−Φ+π},ϕ(eα)∈Lα.

By Step 3,we may assume that α/∈Δ.We need to prove thatwhere bj∈F.For any i=1,2,···,l,by the equality

we have[aαeα+tα,eαi]=[eα,λeαi]by Step 3.Comparing the coefficients of eαion the both sides of the equality(6),we have αi(tα)=0.By the def i nition of dγ,αi(tα)=.Thus=0 for any i=1,2,···,l,and so aαeα∈Lα.

Step 5For any α∈Φ+∪{−Φ+π},ϕ(eα)=λeα.

By Step 3,we may assume that α/∈Δ.We prove it in the following three cases

Case 1α∈Φ+π∩Δ.

Case 2α∈Φ+−Δ.

There is some αk∈Δ,such that α−αk∈Φ+.By the result of Case 1,ϕ(e−αk)=λe−αk. So by the equality

we have[aαeα,e−αk]=[eα,λe−αk].Since[eα,e−αk]=Nα,−αkeα−αk/=0,then aα=λ.So ϕ(eα)=λeαfor any α∈Φ+−Δ.

Case 3α∈Φ+π−Δ.

There is some αs∈Δ,such that α−αs∈Φ+π.By the equality

we have[a−αe−α,eαs]=[e−α,λeαs].Since[e−α,eαs]/=0,then a−α=λ.So ϕ(e−α)=λe−αfor any α∈Φ+π−Δ.

Thus by the results of the above three cases,Step 5 holds.

Step 6For any h∈η,ϕ(h)=λh.

For any i=1,2,···,l,we have the equality

By Step 1,ϕ(h)∈η.By the above equality(10),we have αi(ϕ(h))=λαi(h)=αi(λh)for any i=1,2,···,l.In other words,αi(ϕ(h)−λh)=0 for any i=1,2,···,l.Thus ϕ(h)=λh.

Step 7ϕ=λ·1Pπ.

Since Pπ=

Feβ,then by Step 5,Step 6 and the linearity of ϕ,Step 7 holds.

§3.Applications

Recall that an automorphism ϕ of Pπis def i ned as a linear invertible map ϕ:Pπ→Pπsuch that ϕ([x,y])=[ϕ(x),ϕ(y)]for any x,y∈Pπand a derivation ϕ of a Lie algebra Pπis def i ned as a linear map ϕ:Pπ→Pπsuch that ϕ([x,y])=[ϕ(x),y]+[x,ϕ(y)]for any x,y∈Pπ.We determine the commuting automorphisms and the commuting derivations as applications of the main theorem.

Corollary 1Let ϕ be a commuting automorphism of Pπ.Then ϕ=1Pπ.

ProofBy Theorem,we may assume that ϕ=λ·1Pπfor some λ∈F.Obviously, ϕ(0)=0=1Pπ(0).

By[7,Lemma 3.3],CPπ(Pπ)=0,where CPπ(Pπ)={x∈Pπ|[x,y]=0 for any y∈Pπ}.For any 0/=x∈Pπ,since there is some y∈Pπsuch that[x,y]/=0.By the equality

we have λ[x,y]=[λx,λy]=λ2[x,y].So λ2=λ.Thus λ=0 or 1.By the invertibility of ϕ, λ=1.Thus ϕ(x)=x=1Pπ(x)and so the corollary follows.

Corollary 2Let ϕ be a commuting derivation of Pπ.Then ϕ=0.

ProofBy Theorem,we may assume that ϕ=λ·1Pπ,λ∈F.Obviously,ϕ(0)=0.For any 0/=x∈Pπ,we choose y∈Pπsuch that[x,y]/=0.By the equality

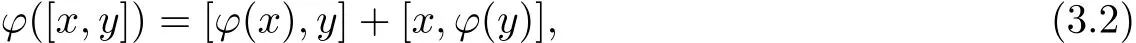
we have λ[x,y]=[λx,y]+[x,λy]=2λ[x,y].So λ=0.Thus ϕ(x)=0 and so the corollary follows.

[1]BENKOVICˇD,EREMITA D.Commuting traces and commutativity preserving maps on triangular algebras[J].J Algebra,2004,280(2):797-824.

[2]BRESˇAR M.Commuting traces of biadditive maps,commutativity-preserving mappings and Lie mappings[J].Trans Amer Math Soc,1993,335(2):525-546.

[3]BRESˇAR M.Commuting maps:a survey[J].Taiwanese J Math,2004,8(3):361-397.

[4]BRESˇAR M,MIERS C R.Commuting maps on Lie ideals[J].Comm Algebra,1995,23(14):5539-5553.

[5]BRESˇAR M,SˇEMRL P.Commuting traces of biadditive maps revisited[J].Comm Algebra,2003,31(1): 381-388.

[6]CHEN Zheng-xin,WANG Deng-yin.Nonlinear maps satisfying derivability on standard parabolic subalgebras of fi nite-dimensional simple Lie algebras[J].Linear Multilinear Algebra,2011,59(3):261-270.

[7]CHEN Zheng-xin,XIAO Zhan-kui.Nonlinear Lie triple derivations on standard parabolic subalgebras of if nite-dimensional simple Lie algebras[J].Linear Multilinear Algebra,2012,60(6):645-656.

[8]CHEUNG Wai-shun.Commuting maps of triangular algebras[J].J London Math Soc,2001,63(1):117-127.

[9]DIVINSKY N.On commuting automorphisms of rings[J].Trans Roy Soc Canada Sect III,1955,49:19-22.

[10]HUMPHREYS J E.Introduction to Lie Algebras and Representation Theory[M].New York:Springer,1972.

[11]LEE Pjek-hwee,WONG Tsai-lien,LIN Jer-shyong,et al.Commuting traces of multiadditive mappings[J]. J Algebra,1997,193(2):709-723.

[12]LEE Tsiu-kwen.σ-commuting mappings in semiprime rings[J].Comm Algebra,2001,29(7):2945-2951.

[13]LEE Tsiu-kwen,LEE Tsong-cherng.Commuting additive mappings in semiprime rings[J].Bull Inst Math Acad Sinca,1996,24(4):259-268.

[14]LUH J.A note on commuting automorphisms of rings[J].Amer Math Monthly,1970,77(1):61-62.

[15]VUKMAN J.Commuting and centralizing mappings in prime rings[J].Proc Amer Math Soc,1990,109(1): 47-52.

[16]XIAO Zhan-kui,WEI Feng.Commuting mappings of generalized matrix algebras[J].Linear Algebra Appl, 2010,433(12):2178-2197.

tion:17B20,17B40

1002–0462(2014)04–0516–07

date:2012-12-25

Supported by the National Natural Science Foundation of China(11101084);Supported by the Fujian Province Natural Science Foundation of China

Biography:CHEN Zheng-xin(1976-),male,native of Qichun,Hubei,an associate professor of Fujian Normal University,Ph.D.,engages in Representation theory of algebra.

CLC number:O151.2Document code:A