Strong Law of Large Numbers for Array of Rowwise AANA Random Variables
CHEN Zhi-yong,LIU Ting-ting,WANG Xue-jun,LI Xiao-qin
(School of Mathematical Science,Anhui University,Hefei 230601,China)
Strong Law of Large Numbers for Array of Rowwise AANA Random Variables
CHEN Zhi-yong,LIU Ting-ting,WANG Xue-jun,LI Xiao-qin
(School of Mathematical Science,Anhui University,Hefei 230601,China)
In this article,the strong laws of large numbers for array of rowwise asymptotically almost negatively associated(AANA)random variables are studied.Some sufficient conditions for strong laws of large numbers for array of rowwise AANA random variables are presented without assumption of identical distribution.Our results extend the corresponding ones for independent random variables to case of AANA random variables.
AANA random variables;array of rowwise AANA random variables;strong law of large numbers
§1.Introduction
Let{Xn,n≥1}be a sequence of random variables def i ned on a f i xed probability space (Ω,F,P).We say that the sequence{Xn,n≥1}satisf i es the strong law of large numbers if there exist some increasing sequence{an,n≥1}and some sequence{cn,n≥1}such that
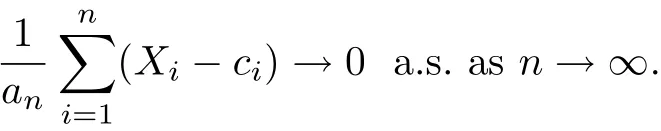
Many authors have extended the strong law of large numbers for sequences of random variables to the case of triangular array of random variables and array of rowwise randomvariables.In the case of independent random variables,Hu and Taylor[1]proved the following strong law of large numbers.
Theorem 1.1 Let{Xni,1≤i≤n,n≥1}be a triangular array of rowwise independent random variables.Let{an,n≥1}be a sequence of positive real numbers such that 0<an↑∞. Let g(t)be a positive,even function such that g(|t|)/|t|pis an increasing function of|t|and g(|t|)/|t|p+1is a decreasing function of|t|,respectively,that is,

for some nonnegative integer p.If p≥2 and
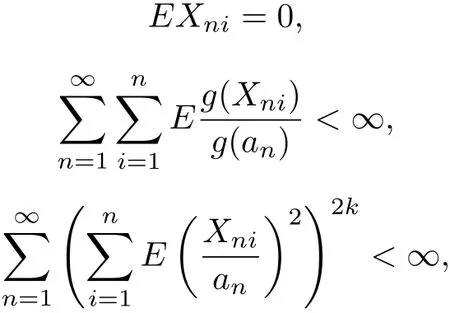
where k is a positive integer,then
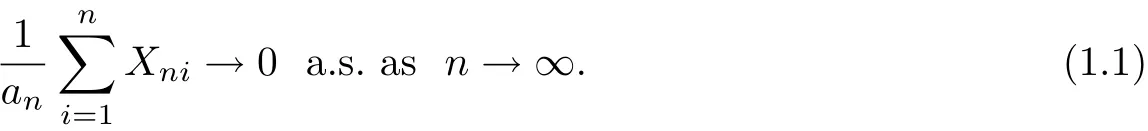
Zhu[2]generalized and improved the result of Hu and Taylor[1]for triangular array of rowwise independent random variables to the case of arrays of rowwise˜ρ-mixing random variables. Shen[3]provided some sufficient conditions to prove the strong law of large numbers for array of negatively orthant dependent random variables.Shen and Hu[4]investigated that some strong law of large numbers for array of rowwise˜ρ-mixing random variables under some simple and weak conditions.Zhou et al[5]obtained some Marcinkiewicz-Zygmund type strong laws of large numbers.
In this article,we consider the strong law of large numbers for array of rowwise asymptotically almost negatively associated random variables.Firstly,let us recall this def i nition.
Def i nition 1.1A sequence{Xn,n≥1}of random variables is called asymptotically almost negatively associated(AANA)if there exists a nonnegative sequence q(n)→0 as n→∞such that
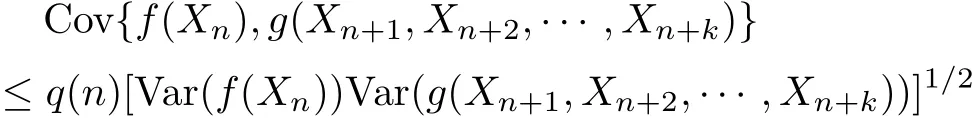
for all n,k≥1 and for all coordinatewise nondecreasing continuous functions f and g whenever the variances exist.
An array of random variables{Xni,n≥1,i≥1}is called rowwise AANA if for every n≥1, {Xni,i≥1}is a sequence of AANA random variables.
Since the concept of AANA random variables was introduced by Chandra and Ghosal[6], many applications have been found.See for example,Chandra and Ghosal[6]derived the Kolmogorov-type inequality and the Marcinkiewcz-Zygmund-type strong law of large numbers, Chandra and Ghosal[7]obtained the almost sure convergence of weighted averages,Ko et al[8]studied the H´ajeck-R`enyi type inequality and Wang et al[9]established the law of the iterated logarithm for product sums.Yuan and An[10]established some Rosenthal-type inequalities for maximum partial sums of AANA sequences.Wang et al[11]studied some convergence properties for AANA sequence.Wang et al[12]generalized and improved the results of Ko et al[8], and studied the large deviation and Marcinkiewicz type strong law of large numbers for AANA sequences.Yang et al[13]investigated the complete convergence of moving average process for AANA sequence,and so forth.
The main purpose of the paper is to further study the strong law of large numbers for array of rowwise AANA random variables.We will present some simple conditions to prove the strong law of numbers.The techniques used in the paper are the truncated method and the Rosenthal-type inequality of AANA random variables.
§2.Preliminary Lemmas
Lemma 2.1[10]Let{Xn,n≥1}be a sequence of AANA random variables with mixing coefficients{q(n),n≥1}and let f1,f2,···be all nondecreasing(or nonincreasing)continuous functions.Then{fn(Xn),n≥1}is still a sequence of AANA random variables with mixing coefficients{q(n),n≥1}.
Lemma 2.2[11]Let 1<p≤2 and{Xn,n≥1}be a sequence of AANA random variables with mixing coefficients{q(n),n≥1}.Assume that EXn=0 for all n≥1 and then there exists a positive constant Cpdepending only on p such that
§3.Main Results and Their Proofs
Let{Xni,i≥1,n≥1}be an array of rowwise AANA random variables with the mixing coefficients{q(n),n≥1}in each row.Throughout this paper,let I(A)be the indicator function of the set A.C denotes a positive constant which may be dif f erent in various places.
Theorem 3.1Let{Xni,i≥1,n≥1}be an array of rowwise AANA random variables withand{an,n≥1}be a sequence of positive real numbers.Assume that {gn(t),n≥1}is a nonnegative sequence of even functions such that gn(|t|)is an increasingfunction of|t|and gn(|t|)/|t|is a decreasing function of|t|for every n≥1 and gn(|t|)>0 for t>0,that is
If

then for any ε>0,

ProofFor f i xed n≥1,def i ne
By Lemma 2.1,we can see that for fi xed n≥1,{),i≥1}is still a sequence of AANA random variables with mixing coefficient{q(n),n≥1}.It is easy to check that for any ε>0,
which implies that

Firstly,we will show that
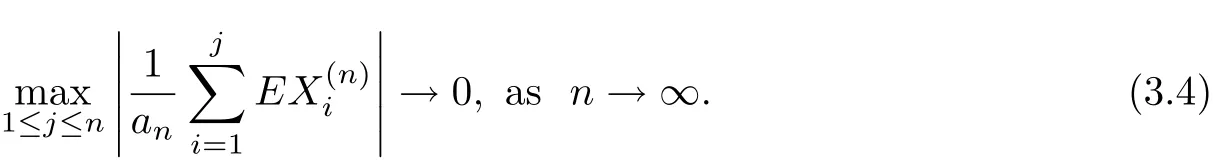
Actually,by conditions gn(|t|)↑,gn(|t|)/|t|↓as|t|↑and(3.1),we have that

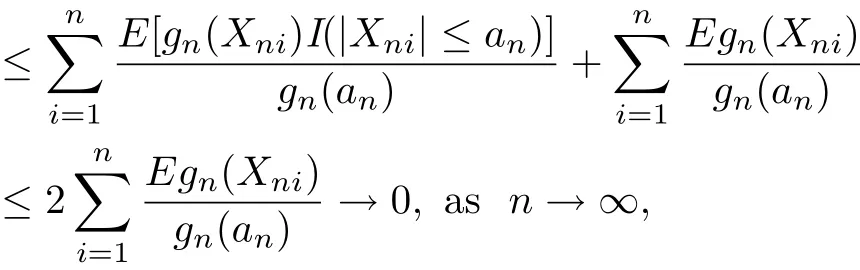
which implies(3.4).It follows from(3.3)and(3.4)that for n large enough,
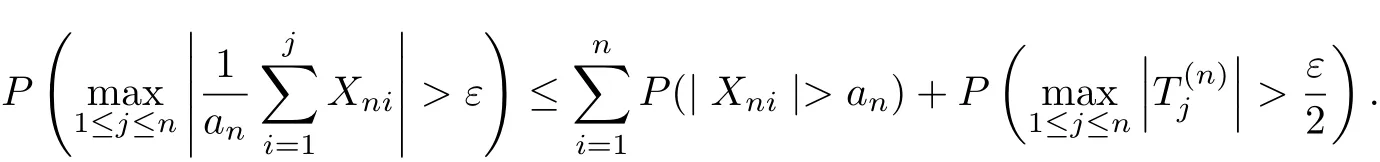
Hence,to prove(3.2),we only need to show that
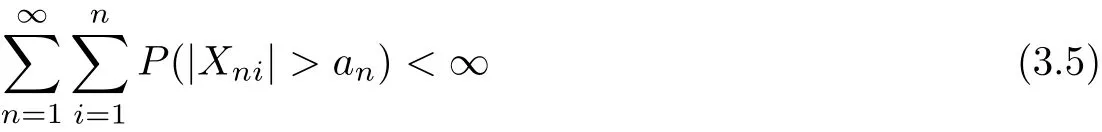
and
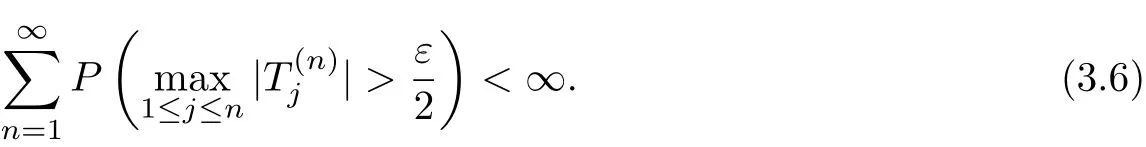
The conditions gn(|t|)↑as|t|↑,Markov’s inequality and(3.1)yield that
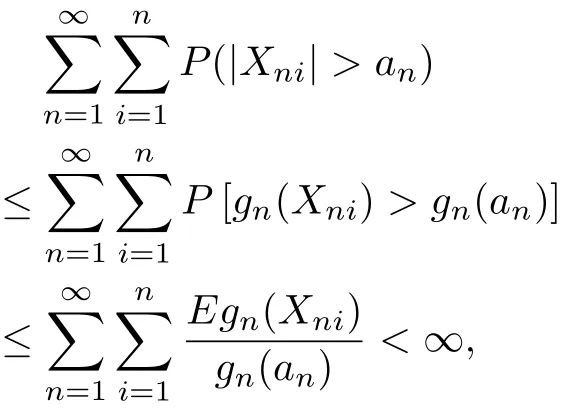
which implies(3.5).
Meanwhile,by Markov’s inequality,Lemma 2.2 with p=2,gn(|t|)↑,gn(|t|)/|t|↓as|t|↑and(3.1),we can get that

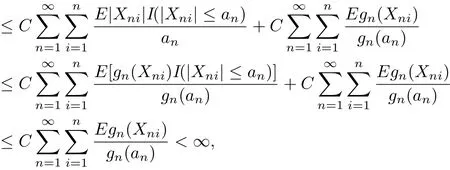
which implies(3.6).This completes the proof of the theorem.
Combining Theorem 3.1 with Borel-Cantelli lemma,we can get the following corollary.
Corollary 3.1Under the conditions of Theorem 3.1,we have
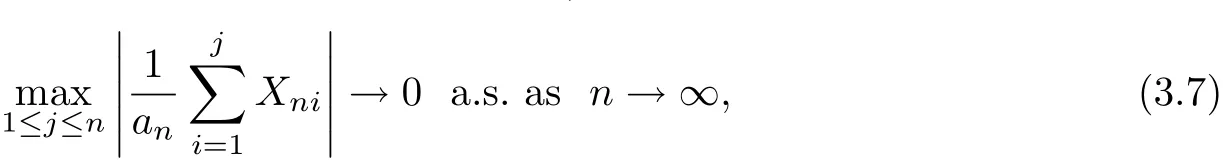
which implies(1.1).
Theorem 3.2Let{Xni,i≥1,n≥1}be an array of rowwise AANA random variables with<∞and{an,n≥1}be a sequence of positive real numbers.Let{gn(t),n≥1} be a nonnegative sequence of even functions such that gn(|t|)is an increasing function of|t|for every n≥1.Assume that there exists a constant α>0 such that gn(t)≥αt for 0<t≤1.If

then for any ε>0,(3.2)holds.
ProofWe use the same notation as that in Theorem 3.1.The proof is similar to that of Theorem 3.1.Firstly,we will show that(3.4)holds.In fact,by the conditions of gn(t)≥αt for 0<t≤1 and(3.8),we have that
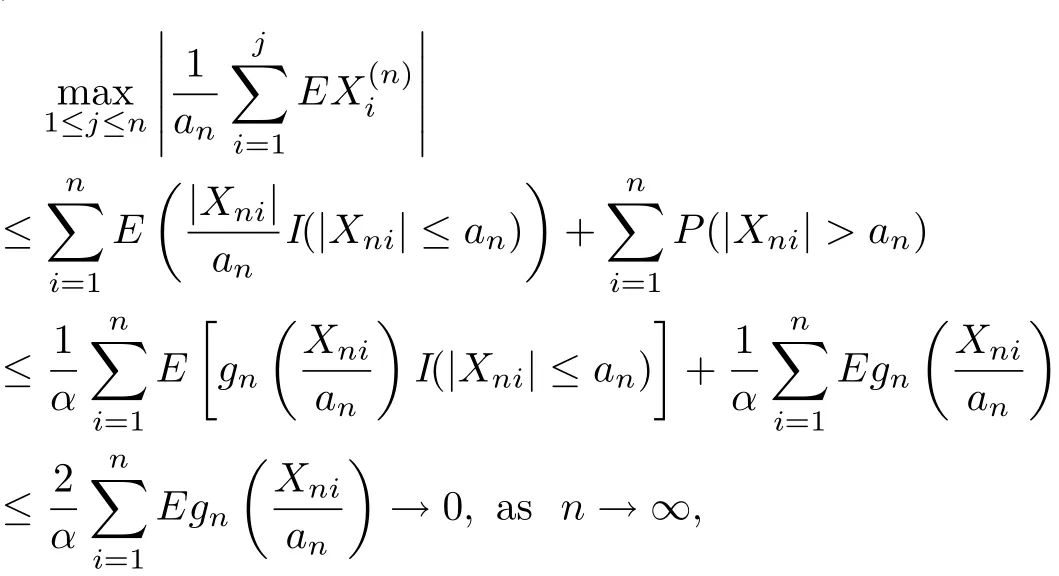
which implies(3.4).According to the proof of Theorem 3.1,we only need to prove that(3.5) and(3.6)hold.
Secondly,for|Xni|>an>0,we have gnBy gn(|t|)↑as|t|↑,Markov’s inequality and(3.8),we can get that
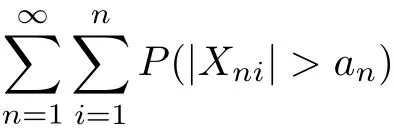
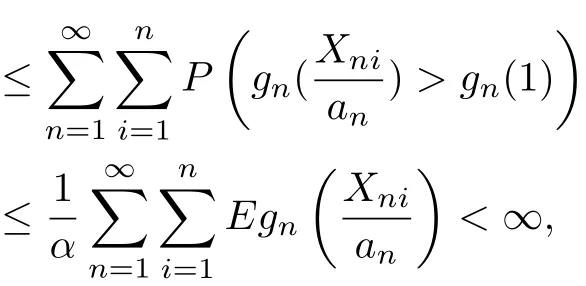
which implies(3.5).
On the other hand,by Markov’s inequality,Lemma 2.2 with p=2,gn(t)≥αt for 0<t≤1 and(3.8),we can get that which implies(3.6).This completes the proof of the theorem.
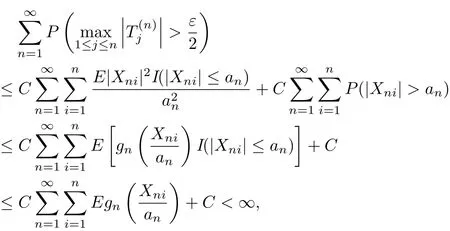
Corollary 3.2Under the conditions of Theorem 3.2,(3.7)holds.
Theorem 3.3Let{Xni,i≥1,n≥1}be an array of rowwise AANA random variables with<∞and{an,n≥1}be a sequence of positive real numbers.EXni=0,i≥ 1,n≥1.Let{gn(t),n≥1}be a sequence of nonnegative,even functions.Assume that there exist β∈[1,2]and α>0 such that gn(x)≥αxβfor 0<x≤1 and exists α>0 such that gn(x)≥αx for x>1.If(3.8)satisf i es,then for any ε>0,(3.2)holds.
ProofThe proof is similar to that of Theorem 3.1 and we use the same notation as that in Theorem 3.1.Firstly,it shows that(3.4)holds.By the conditions of EXni=0,gn(x)≥αx for x>1 and(3.8),it follows
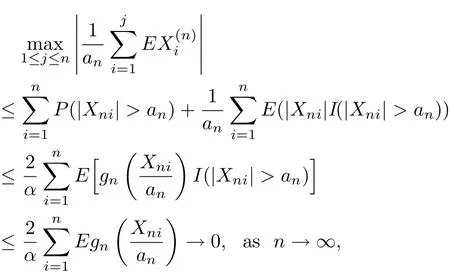
which implies(3.4).Hence,to prove(3.2),it needs to show that(3.5)and(3.6)hold true.
Obviously,the conditions gn(x)≥αx for x>1 and(3.8)yield that
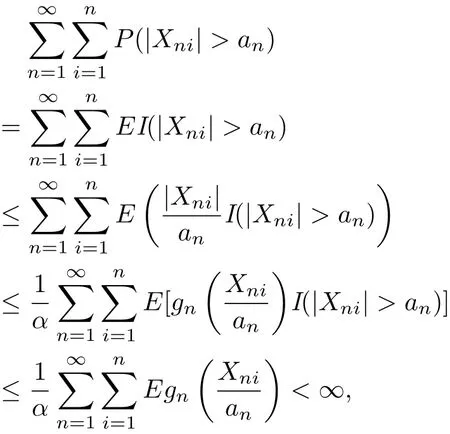
which implies(3.5).
Meanwhile,by Markov’s inequality,Lemma 2.2 with p=2,gn(x)≥αxβfor 1≤β≤2,0<x≤1 and(3.8),it follows that

which implies(3.6).This completes the proof of the theorem.
Corollary 3.3Under the conditions of Theorem 3.3,(3.7)holds.
Theorem 3.4Let{Xni,i≥1,n≥1}be an array of rowwise AANA random variables with<∞and{an,n≥1}be a sequence of positive real numbers.Let{gn(t),n≥ 1}be a nonnegative sequence of even functions.Assume that there exists an α>0 such that gn(x)≥αx for x>0.If(3.8)satisf i es,then for any ε>0,(3.2)holds.
ProofWe use the same notation as that in Theorem 3.1.By the conditions of gn(x)≥αx for x>0 and(3.8),it has that

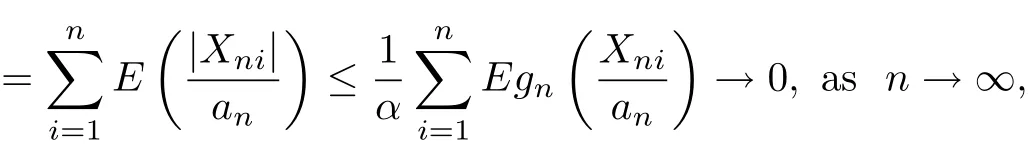
which implies(3.4).Hence,to prove(3.2),we only need to show that(3.5)and(3.6)hold true.
Obviously,the conditions gn(x)≥αx for x>0 and(3.8)yield that
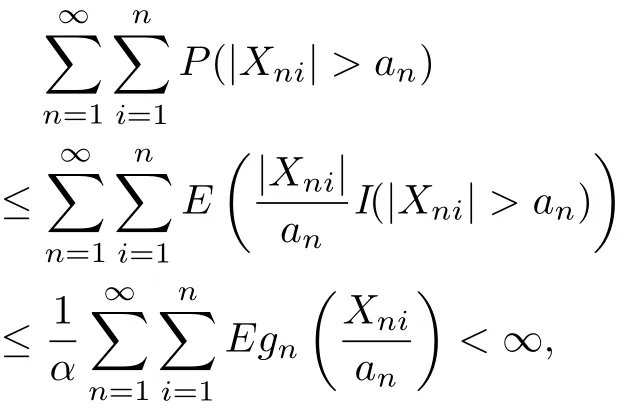
which implies(3.5).
Meanwhile,by Markov’s inequality,Lemma 2.2 with p=2,gn(x)≥αx for x>0 and(3.8), it can be checked that which implies(3.6).This completes the proof of the theorem.
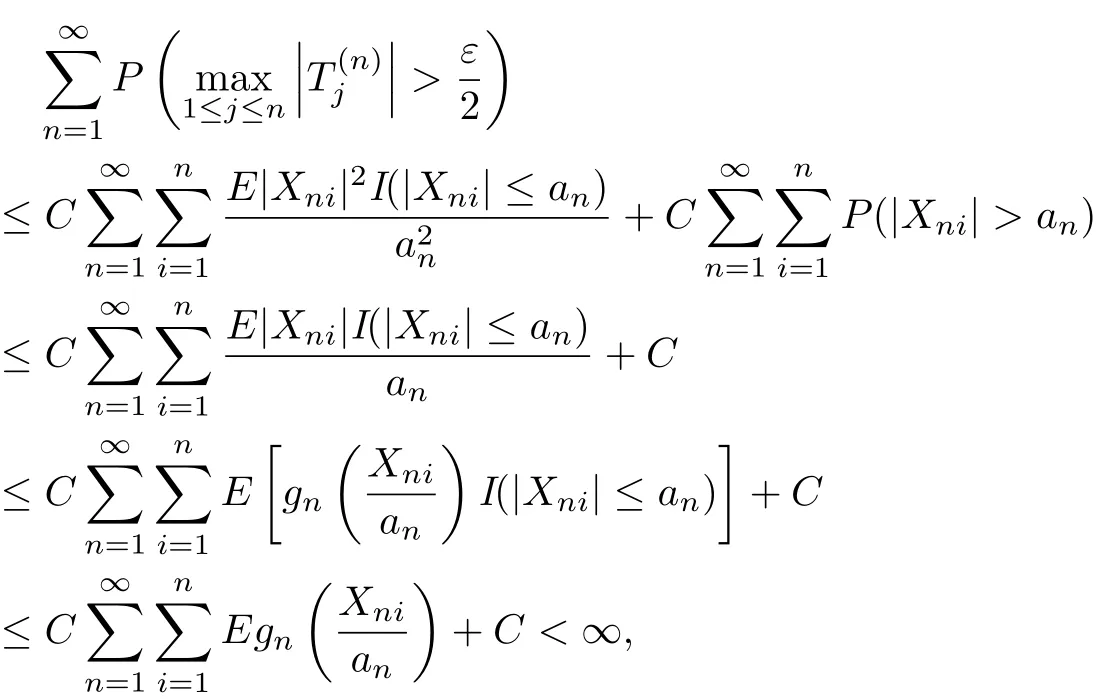
Corollary 3.4Under the conditions of Theorem 3.4,(3.7)holds.
Theorem 3.5Let{Xni,i≥1,n≥1}be an array of rowwise AANA random variables with<∞and{an,n≥1}be a sequence of positive real numbers.Let{gn(t),n≥1} be a nonnegative sequence of even functions.Assume that there exist β∈[2,∞)and α>0 such that gn(x)≥αxβfor x>0.If
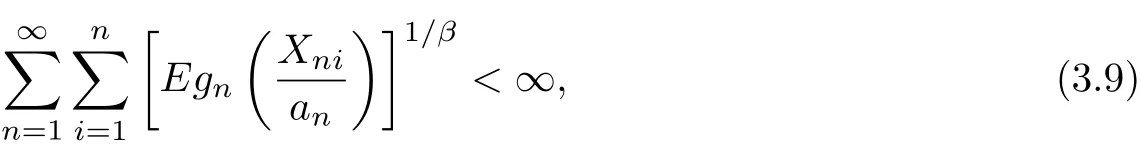
then for any ε>0,(3.2)holds.
ProofIt is used the same notation as that in Theorem 3.1.One can see that(3.9)implies that

and
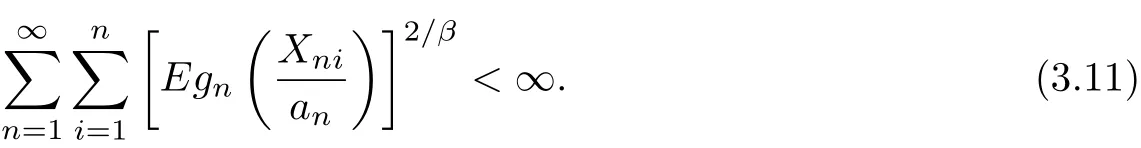
Firstly,it shows that(3.4)holds.In fact,by H¨older’s inequality,gn(x)≥αxβfor β≥2,x>0,(3.9)and(3.10),it has

which implies(3.4).Hence,to prove(3.2),we only need to show that(3.5)and(3.6)hold true. Secondly,by the conditions gn(x)≥αxβfor β≥2,x>0 and(3.10),it can be seen that

which implies(3.5).
Meanwhile,by Markov’s inequality,Lemma 2.2 with p=2,H¨older’s inequality,gn(x)≥αxβfor β≥2,x>0 and(3.11),we obtain that
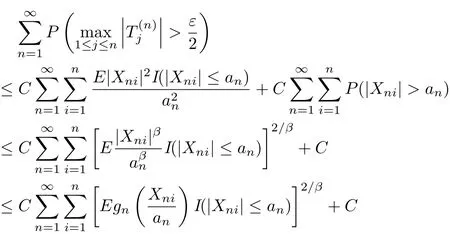
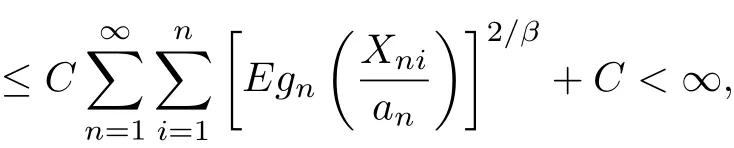
which implies(3.6).This completes the proof of the theorem.
Corollary 3.5 Under the conditions of Theorem 3.5,(3.7)holds.
[1]HU T C,TAYLOR R L.On the strong law for arrays and for the bootstrap mean and variance[J].International Journal of Mathematics and Mathematical Sciences,1997,20:375-382.
[2]ZHU Meng-hu.Strong laws of large numbers for arrays of rowwise˜ρ-mixing random variables[J].Discrete Dynamics in Nature and Society,2007,2007(1):1-6.
[3]SHEN Ai-ting.Some strong limit theorems for arrays of rowwise negatively orthant-dependent1 random variables[J].Journal of Inequalities and Applications,2011,2011(1):1-11.
[4]SHEN Ai-ting,HU shu-he.A note on the strong law of large numbers for arrays of rowwise˜ρ-mixing random variables[J].Discrete Dynamics in Nature and Society,2011,2011(1):1-9.
[5]ZHOU Xing-cai,LIN Jin-guan,WANG Xue-jun,et al.On complete convergence for arrary of rowwise strong mixing random variables[J].Communications in Mathematical Research,2011,27:234-242.
[6]CHANDRA T K,GHOSAL S.Extensions of the strong law of large numbers of Marcinkiewicz and Zygmund for dependent variables[J].Acta Mathematica Hungarica,1996a,71:327-336.
[7]CHANDRA T K,GHOSAL S.The strong law of large numbers for weighted averages under dependence assumptions[J].Journal of Theoretical Probability,1996b,9:797-809.
[8]KO M H,KIM T S,LIN Zheng-yan.The H´ajeck-R`enyi inequality for the AANA random variables and its applications[J].Taiwanese Journal of Mathematics,2005,9:111-122.
[9]WANG Yue-bao,YAN Ji-gao,CHENG Feng-yang,et al.The strong law of large numbers and the law of the iterated logarithm for product sums of NA and AANA random variables[J].Southeast Asian Bulletin of Mathematics,2003,27:369-384.
[10]YUAN D M,AN J.Rosenthal type inequalities for asymptotically almost negatively associated random variables and applications[J].Science in China Series A:Mathematics,2009,52:1887-1904.
[11]WANG Xue-jun,HU Shu-he,YANG Wen-zhi.Convergence properties for asymptotically almost negatively associated sequence[J].Discrete Dynamics in Nature and Society,2010,2010(1):1-15.
[12]WANG Xue-jun,HU Shu-he,LI Xiao-qin,et al.Maximal inequalities and strong law of large numbers for AANA sequences[J].Communications of the Korean Mathematical Society,2011,26:151-161.
[13]YANG Wen-zhi,WANG Xue-jun,LING Neng-xiang,et al.On complete convergence of moving average process for AANA sequence[J].Discrete Dynamics in Nature and Society,2012,2012(1):1-24.
tion:60F15
1002-0426(2014)04-0475-11
date:2013-04-02
Supported by the National Natural Science Foundation of China(11171001,11201001); Supported by the Natural Science Foundation of Anhui Province(1208085QA03);Supported by the Talents Youth Fund of Anhui Province Universities(2012SQRL204);Supported by th Doctoral Research Start-up Funds Projects of Anhui University(33190250)
Biography:CHEN Zhi-yong(1986-),male,native of Putian,Fujian,M.S.D.,engages in probability limit theorem.
CLC number:O211.4Document code:A
 Chinese Quarterly Journal of Mathematics2014年4期
Chinese Quarterly Journal of Mathematics2014年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- On the Cycle Structure of Iteration Graphs over the Unit Group
- On the Strong Rates of Convergence for Arrays of Rowwise Extended NegativelyDependent Random Variables
- Some Notes on G-cone Metric Spaces
- On Laguerre Isopararmetric Hypersurfaces in ℝ7
- On a Discrete Fractional Boundary Value Problem with Nonlocal Fractional Boundary Conditions
- Fast Parallel Method for Polynomial Evaluation at Points in Arithmetic Progression
