数控机床定位误差全温度综合建模及实时补偿*
朱小龙,杨建国,代贵松
(上海交通大学 机械与动力工程学院,上海 200240)
数控机床定位误差全温度综合建模及实时补偿*
朱小龙,杨建国,代贵松
(上海交通大学 机械与动力工程学院,上海 200240)
提出一种数控机床定位误差的全温度综合建模方法。通过测量获得加工中心定位误差,采用多项式拟合和纵向建模法建立了加工中心在不同温度状态下定位误差的综合预测模型。利用FANUC数控系统的外部原点偏移功能,对一台加工中心进行实时误差补偿实验验证。实验结果表明,应用此误差建模方法及补偿功能,在常温和温升状态下,加工中心在三个方向的定位误差与补偿前相比都下降90%左右,大幅提高了加工中心在变温状态下的定位精度。
加工中心;定位误差;误差建模与补偿
0 引言
高精密加工在当今工业应用中占有举足轻重的作用,已经成为国际竞争力的重要标志。在机械加工过程中,机床的误差将会直接影响工件的加工精度。定位误差是影响机床精度的重要因素之一[1]。考虑到机床温度场对定位精度影响较大[2],因此对机床不同温度状态下的定位误差进行研究是极其有意义的。
机床温度和定位误差检测的目的是为了获取机床温度场和变形位移场的信息,建立定位误差预测模型并对定位误差实时补偿提供理论依据。通常误差补偿是在某一温度下建立的误差预测模型基础上进行的,而没有考虑到由于机床温度的变化引起的机床定位误差变化,这也就是为什么一般补偿的效果不明显[3]。因此需要对机床各种温度条件下的定位误差建模问题作进一步的研究。
本文使用激光干涉仪对一台加工中心从常温到热平衡状态的全温度条件下的定位误差进行了测量,并运用线性拟合及纵向建模综合建模方法对一台加工中心的定位误差进行建模,从而建立了对加工中心定位误差的高精度综合预测模型。最后在加工中心上,基于FANUC数控系统的外部原点偏移功能,对加工中心常温及温升状态下的定位误差进行实时误差补偿实验。在加工中心上的误差实时补偿实验表明,文中采用的误差建模方法及实时补偿功能能够大幅提高加工中心的定位精度。
1 误差测量
加工中心移动轴定位误差的测量采用激光干涉仪,如图1所示。为了减少测量过程中的随机误差,对每个轴的定位误差分别重复测量三次,并取测量的平均值作为最终定位误差的测量结果[4]。加工中心主轴最大转速8000rpm,快速进给速度33m/min,X/Y/Z轴行程分别为850/560/650mm。

图1 定位误差的测量
本文以加工中心X轴定位误差的测量、建模为例进行说明。考虑到数控加工中心在不同温度下的定位误差是不同的[5-6],因此必须测量加工中心在不同温度下的定位误差及温度。在采用激光干涉仪对加工中心的定位误差进行测量时,同时测量加工中心关键点的温度,使得每一组关键点的温度对应一组定位误差。在实验测量过程中加工中心空运行,主轴转速40000rpm,X/Y/Z轴进给速度为f=0.2mm/r。为了测量关键点温度,将2个PT100温度传感器加工中心上,其中T1测量X轴丝杠螺母温度,T2测量X轴导轨温度[7]。图2为温度传感器(白色圆圈)实际布置图。

图2 X轴温度传感器的布置
实验中测量数控加工中心从冷态(即刚开机,常温状态下)到热平衡过程中的定位误差及关键点温度,实验一共采集到七组数据。实验测得的加工中心在不同检测时间下的加工中心关键点温度以及定位误差如图3所示。
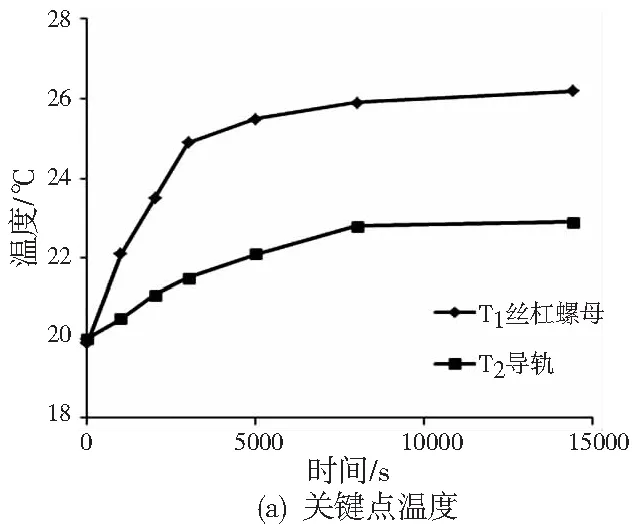

图3 加工中心X方向关键点温度和定位误差
2 误差建模
由图3可见,在不同的温度状态下,加工中心的定位误差分布有很大的变化,且加工中心到达热平衡时间大概在8000s左右。图3可以看出,加工中心在不同的温度下,X方向的定位误差是不同的,有明显的变化,这也就是为什么实际切削过程中一般误差补偿效果不太明显的原因。因为其补偿主要是常温下的定位误差,而在实际切削加工过程中,定位误差是随机床温度场变化而变化的。如图3所示,加工中心定位误差随着关键点温度和坐标位置的变化而变化,是一种与机床坐标和机床温度有关的误差。考虑到不同时刻,定位误差是与温度相关的,将机床定位误差被分为两类:与位置有关的定位误差,与位置无关的定位误差[8-9]。与位置无关的定位误差,是由于机床温度场的作用,而与位置有关的定位误差则是温度和位置的综合作用。考虑到这些原因,需要建立不同的模型来预测机床定位误差。与位置无关的定位误差可以按公式(1)表示:
(1)
式中E1(t)代表与位置无关的定位误差,t代表时间,βi为系数,i代表温度传感器编号,Ti(t)表示t时刻下编号为i的温度传感器的温度,N代表温度传感器的数目。
与位置有关的误差可以表示为公式(2):
(2)
式中E2(t)代表与位置有关的定位误差,x为对应相应定位误差的位置。
如果仅仅考虑定位误差与温度的关系,则公式(1)和(2)中E1和E2与温度变量成线性关系,所以可以将公式(1)和(2)合并为:
E=TB
(3)
式中T=[T1(t),T2(t),...,TN(t)]为温度变量矩阵,即在不同时刻下采集的温度数据组,B为相关系数矩阵,可以通过最小二乘法获得。
以X方向为例,采用纵向建模法,即在某一确定的位置x处,对此处随机床温度变化引起的定位误差进行建模。由于在相同位置处,位置对定位误差的影响是相同的,从而按此方法建模时,就可以先不考虑位置对定位误差的影响。故可对某一位置在不同温度下的定位误差按公式(1)进行建模。以X方向的测量中间点x=400mm和最远端x=800mm处的定位误差为例,进行误差建模,可以得到如下定位误差模型:
E400=2.4258T1-2.1313T2
(4)
E800=4.7416T1-3.9864T2
(5)
位置x=400mm和x=800mm处定位误差拟合曲线如图4所示。由x方向x=400mm和x=800mm处定位误差拟合曲线可以看出,上述纵向建模法建立的模型可以很好的对定位误差进行拟合建模,且曲线拟合残差都在很小的范围之内,满足建模的精度要求。
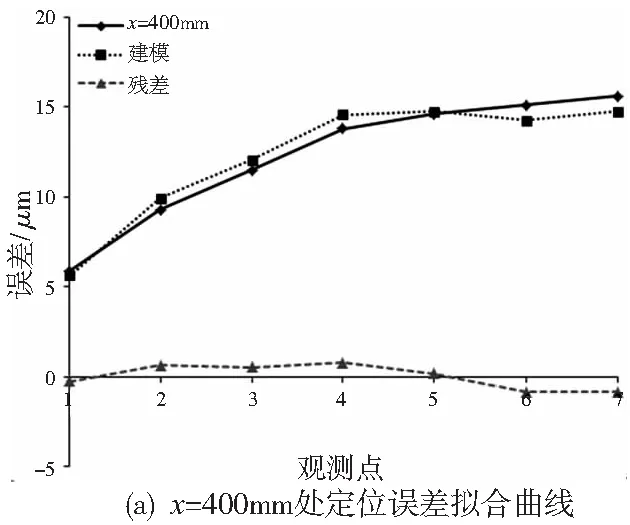
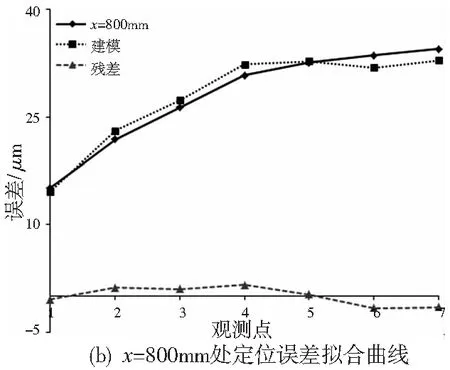
图4 曲线拟合
同样在X方向的其它位置,分别对定位误差进行纵向建模,可以得到X方向的建模系数如下表1所示。
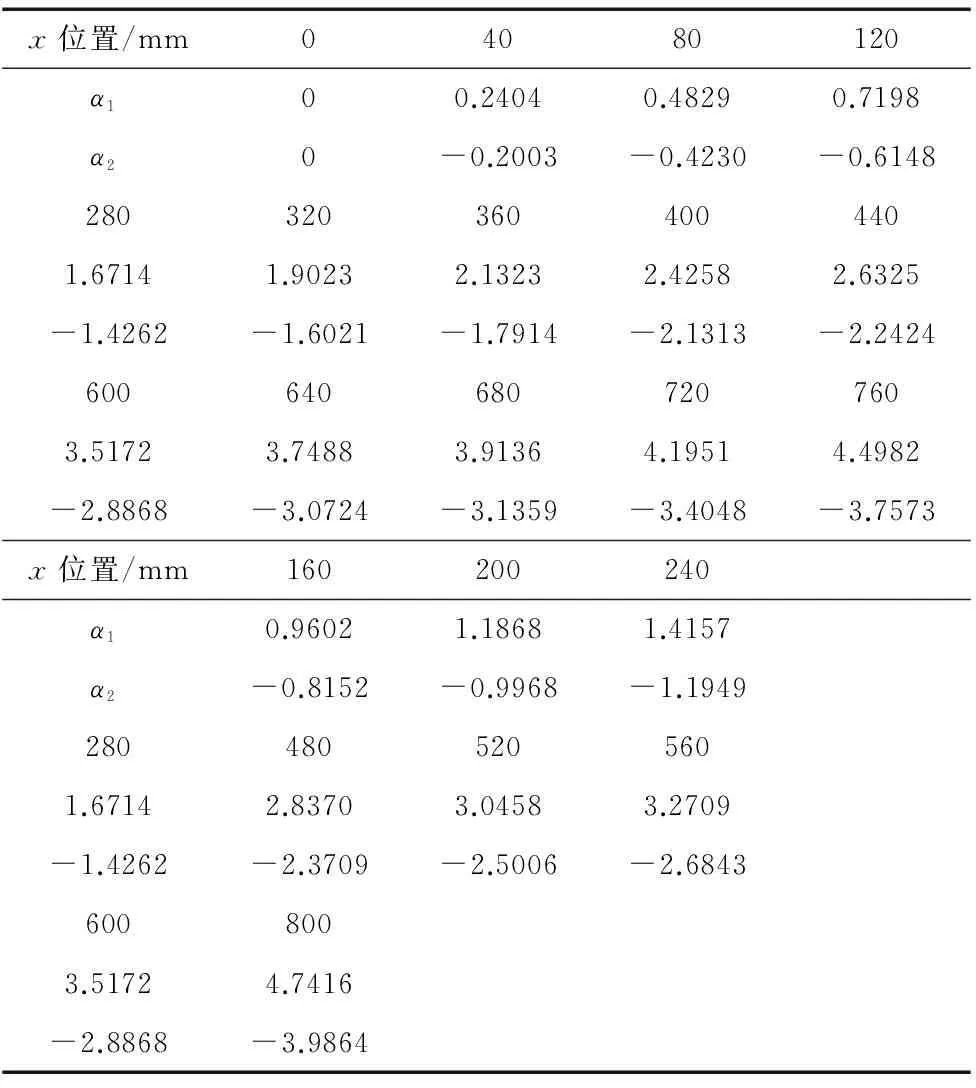
表1 X方向定位误差建模系数
由表1可以看出,误差拟合曲线中的系数α1、α2,在机床沿x方向运动时,呈线性变化,其中α1随x变大而变大,α2随x变大而变小。因而建模系数α1、α2可以分别对x进行一次拟合,拟合结果分别为:
α1=0.00585x+0.0202
(6)
α2=-0.00479x-0.0476
(7)
拟合曲线如图5所示。可以看出,对误差拟合曲线中的系数α1、α2进行线性拟合是合适的,一次拟合的模型能够满足建模的要求。
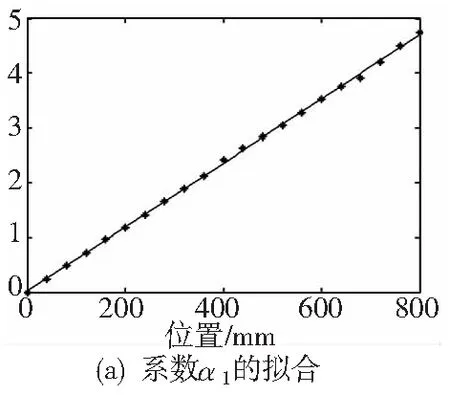

图5 X方向系数的拟合
综合考虑机床温度和位置的影响,根据公式(3)可以得到加工中心X方向在任意位置处,不同温度下的定位误差可以表示为:
Ex=(0.00585x+0.0202)T1+(-0.00479x-0.0476)T2
=[0.0202T1-0.0476T2]+[0.00585xT1-0.00479xT2]
(9)
将从常温状态开始测量定位误差的7次实验的次数作为坐标轴的x轴坐标,移动轴的位置作为y轴坐标,不同温度状态下的定位误差作为z轴坐标,绘制如图6所示示意图,则采用的误差模型的拟合效果如图6a所示。实验有7条误差曲线,共有21×7=147个误差数值,汇总这些误差,其中前21个点为常温下模型拟合残差点,后面以此类推[10]。则X方向定位误差残差示意图如图6b所示,可以看出采用模型的建模精度在[-1.72μm,2.16μm]范围内。
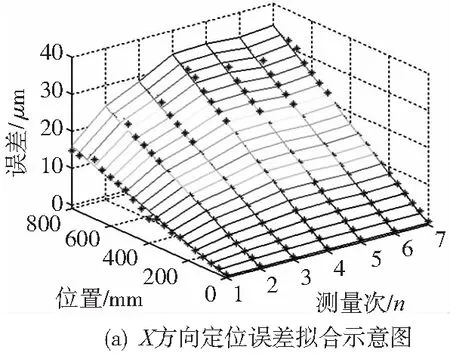
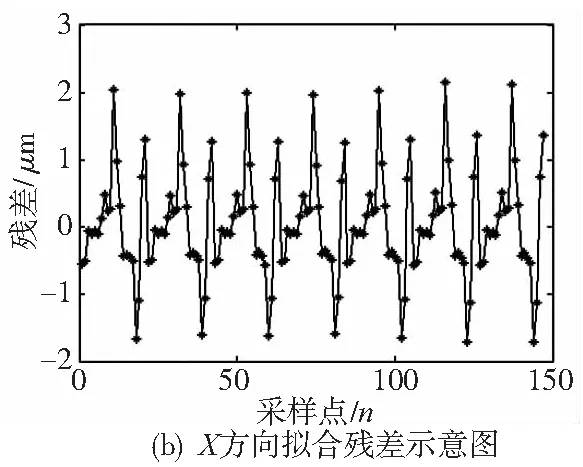
图6 X方向定位误差建模
3 实验
3.1 补偿原理
为了验证模型的有效性,在一台加工中心上进行了误差补偿实验,补偿实验基于FANUC 数控系统的外部坐标原点偏移功能。实验中将不同温度状态下定位误差预测模型计算得到的误差值,通过机床数控系统外部坐标偏移功能加到系统控制信号中,从而实现机床误差的实时补偿[11]。数控系统的外部坐标偏移功能无需修改机床的数控指令,只要在系统PLC中添加部分程序即可,且不会影响原系统。图7为补偿原理框图。
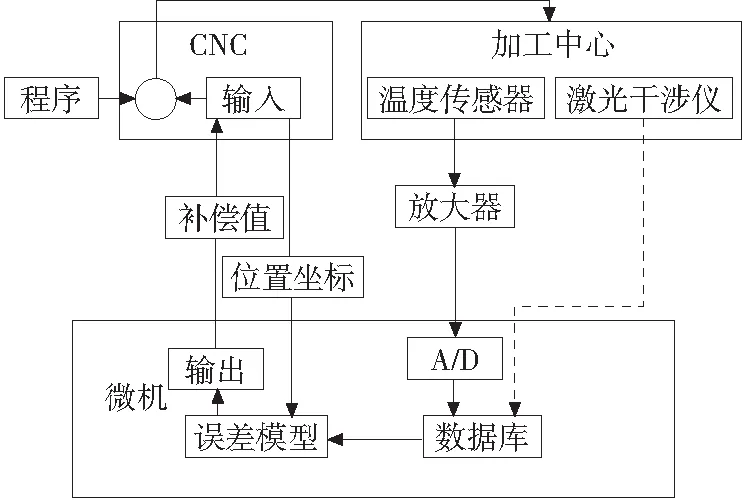
图7 补偿原理图
3.2 补偿实验
将上述方法应用于一台加工中心上,采用激光干涉仪测量加工中心常温状态以及温升状态下补偿前后的定位误差,并对补偿前后效果进行比较。实验结果如图8所示。图8可以看出,上文所提误差建模方法可以准确的预测数控机床在不同温度及不同位置下的定位误差,也就是建立了加工中心从常温状态到热平衡状态下的定位误差预测模型。以X方向为例,补偿后,加工中心常温下最大定位误差由38.3μm下降至4.5μm,误差降低了88.2%左右;温升后最大定位误差由28.6μm下降至3.0μm,误差下降89.4%左右。总的来说,加工中心在常温及温升状态下,误差补偿后与补偿前相比,三个方向的定位误差都下降90%左右,大幅提高了机床的精度。
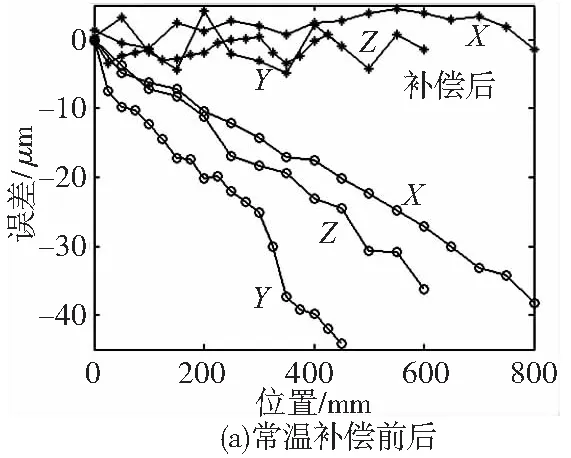
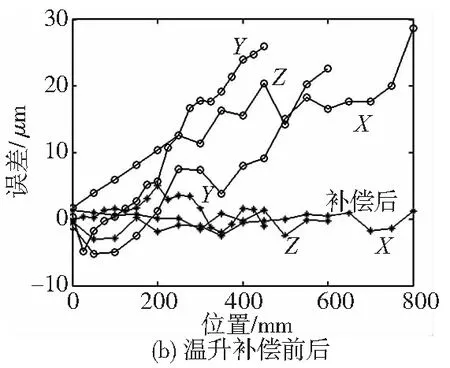
图8 常温及温升补偿前后对比
4 结论
(1)加工中心定位误差建模中使用的多项式拟合及纵向建模法,对加工中心从常温到热平衡的全温度下的定位误差进行建模,获得了高精度的定位误差综合预测模型。采用这种建模方法,可以准确的预测机床处于任意温度状态及任意位置处的定位误差,且具有良好的鲁棒性。
(2)在加工中心上基于FANUC数控系统外部原点偏移功能的实时误差补偿实验表明,此方法具有较好的补偿效果,能够在机床温度变化状态下大幅提高机床精度。
[1] 王福吉,贾振元,阳江源,等. 基于动态模糊神经网络的机床时变定位误差补偿[J].机械工程学报,2011,47(13):175-179.
[2] Wei Wang,Yi Zhang,Jianguo Yang,et al. Geometric and thermal error compensation for CNC milling machines based on Newton interpolation method[J]. Journal of Mechanical Engineering Science,2012,0(0):1-9.
[3] ABDUL W K,CHEN Wuyi. Systematic geometric error modeling for workspace volumetric calibration of a five-axis turbine blade grinding machine[J]. Chinese Journal of Aeronautics,2010,23:604-615.
[4] DU Zhengchun,ZHANG Shujie,Hong Maisheng. Development of a multi-step measuring method for motion accuracy of NC machine tools based on cross grid encoder[J]. International Journal of Machine Tools & Manufacture, 2010, 50: 270-280.
[5] Sina Eskandari,Behrooz Arezoo,Amir Abdullah. Positional,geometrical,and thermal errors compensation by tool path modification using three methods of regression,neural networks,and fuzzy logic[J]. International Journal of Advanced Manufacturing Technology. 2013,65:1635-1649.
[6] 崔岗卫,高栋,姚英学. 重型数控机床热误差的分离与建模[J]. 哈尔滨工业大学学报,2012,44(9):51-56.
[7] Kaiguo Fan,Jianguo Yang,Liyan Yang. Orthogonal Polynomials-based thermally induced spindle and geometric error modeling and compensation[J]. International Journal of Advanced Manufacturing Technology,2013,65:1791-1800.
[8] Jie Zhu,Jun Ni,Albert J. Shih. Robust Machine Tool Thermal Error Modeling Through Thermal Model Concept[J].Journal of Manufacturing Science and Engineering, 2008,130:061006.
[9] J. S. Chen,J. X. Yuan,J. Ni,et al. Real-time Compensation for Time-variant Volumetric Errors on a Machining Center[J].Journal of Manufacturing Science and Engineering,1993,115 (4):472-479.
[10]王维,杨建国,姚晓栋,等.数控机床几何误差与热误差综合建模及实时补偿[J]. 上海交通大学学报,2012,48(7):165-179.
[11]沈金华,李永祥,鲁志政,等. 数控车床几何与热误差综合实时补偿方法应用[J].四川大学学报,2008,40(1):163-166.
(编辑 李秀敏)
Synthesis Modeling and Real-time Compensation of Position Errors at Full Temperature for Machine Tools
ZHU Xiao-long,YANG Jian-guo,DAI Gui-song
(School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240,China)
A synthesis model of positioning error under full temperature for machine tools is presented. Through measuring the positioning error of machining center, a synthesis prediction model for positioning error at different temperatures is proposed based on polynomial fitting and longitudinal modeling. Real-time error compensation is carried out on a machining center by applying the external coordinate offset function of FANUC computer numerical control(CNC) system. The real-time compensation carried out on the machining center shows that application of this compensation method compensates positioning errors in three directions by almost 90% compared with no compensation. The accuracy of the machining center is improved effectively.
machining center;positioning error;error modeling and compensation
1001-2265(2014)05-0083-04
10.13462/j.cnki.mmtamt.2014.05.021
2013-09-06
国家自然科学基金(51275305);高等学校博士学科点专项科研基金(20110073110041)
朱小龙(1988—),男,江苏东台人,上海交通大学硕士研究生,研究方向为数控机床精密加工与测试,(E-mail)wolloy0504@126.com。
TH164;TG659
A

