基于概率有限元法对核电轮槽铣床主轴的可靠性分析

覃才友，黄 娟 ，李小汝

(四川工程职业技术学院 机电工程系， 四川 德阳 618000)

基于概率有限元法对核电轮槽铣床主轴的可靠性分析

覃才友，黄 娟 ，李小汝

(四川工程职业技术学院 机电工程系， 四川 德阳 618000)

针对影响核电轮槽铣床主轴可靠性因素复杂的情况，利用ANSYS参数化建模技术及概率有限元模块PDS建立机床主轴有限元分析模型，将影响机床主轴可靠性的主轴前端直径、弹性模量和扭矩作为随机变量，利用概率有限元法与Monte Carlo模拟方法相结合，对主轴进行可靠性概率有限元计算。得到在置信概率为95%时，三个随机变量的设计变量柱状图、失效概率分布函数、累积分布曲线和灵敏度分析。该方法为机床主轴可靠性分析和设计研究提出了新的思维路径，具有很好的应用前景。

核电轮槽铣床主轴；概率有限元；Monte Carlo模拟；可靠性分析

0 引言

由于核电轮槽铣床主轴采用复合金属材料，材料特性复杂，同时机床在加工轮槽时需要经过粗加工、半精加工、精加工多步工序，需要的主轴功率和扭矩也不相同，因此在分析主轴可靠性的时候必须考虑主轴前端直径、主轴弹性模量和扭矩三个随机变量因素。针对这一特点，提出了基于概率有限元法对核电轮槽铣床主轴的可靠性分析。

1 利用ANSYA建立核电轮槽铣床主轴的有限元模型

核电轮槽铣床的主轴承受着大扭矩的作用，其扭矩达到了8000N.m，因此在设计主轴时，需要充分考虑其加工转子的可靠性[2-3]。主轴材料使用复合金属材料，其弹性模量200GP，密度为(6.15～6.24)×103kg/m3,泊松比为0.57，其它主轴关键零件的几何参数见表1。

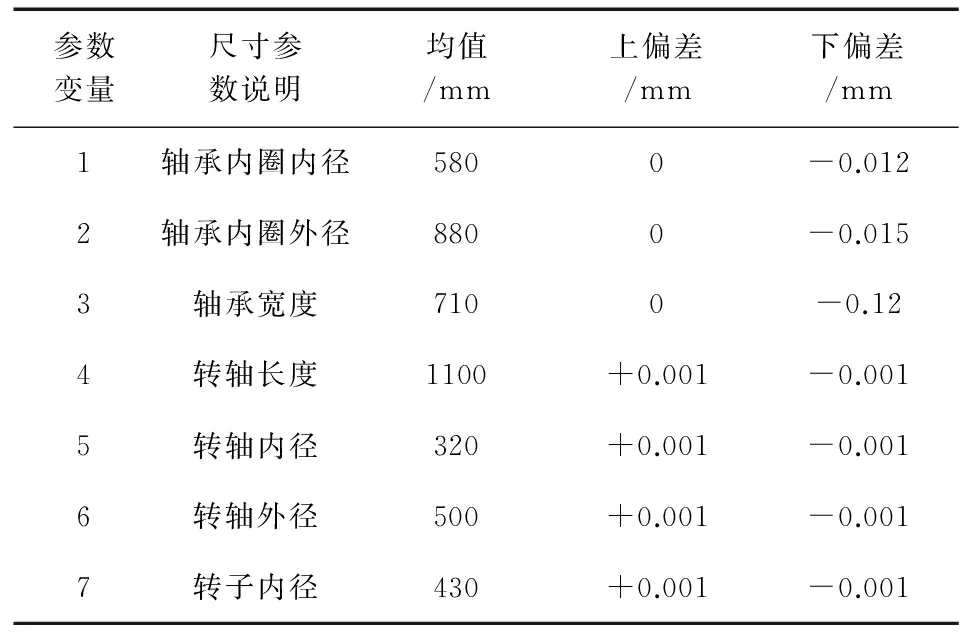
表1 主轴关键零件的几何参数

根据主轴的基本尺寸，忽略掉过渡圆角等对主轴影响小的特征，利用ANSYS/APDL建立主轴的参数化模型，主轴整体网格采用MESH200分网单元和SOLID45八节点实体单元经多次扫掠而成，对轮槽铣床的主轴和轴承简化后，其有限元模型如图1。

图1 核电轮槽铣床主轴有限元模型

2 Monte Carlo模拟理论

Monte Carlo模拟理论是有限元分析中最常用的方法，它能清楚地模拟实际问题的真实行为特征[4-6]。Monte Carlo模拟法的基本思想如下：建立与所研究对象对应的一个随机模型，形成某个随机变量，它的某个数字特征(如概率、期望等)，然后按照随机模型进行大量的随机实验，获得随机变量的大量抽样值，用统计特征求出数字特征的估计值。基于这种思想，设目标函数Z=g(X1,X2…,Xn)，其中Xi为具有某种分布的随机变量。

对Xi(i=1,2,…,N)进行N次随机抽样，得到N组。将第j组值代入目标函数，得到Zj(j=1,2,…,N)值。设N个Zj值中存在Nj个Zj<0，则结构失效的概率为：

(1)

式中：N为抽样总次数；Nf为失效的次数。

②收集河道相关的治理规划和具体实施情况，已建工程相应的建设任务、标准、主要建设内容和工程投资等，河道断面、滩地及堤防上下游、左右岸衔接情况。

假设Z与影响主轴结构的随机参数矢量X=(X1,X2,…,XN)的关系可用含有交叉项的二次函数描述，如式(2)。

(2)

式中：α0、αi、αij(i=1,2,…,N;i=j,…,N)—待定系数，共n+1+n(n+1)/2个。

核电轮槽铣床主轴的失效可以认为是其最大弯曲变形超过其许用的变形，从而影响了核电轮槽铣床加工精度。假定设计要求的主轴最大弯曲变形为LMax,则极限状态函数为：

(3)

该式表示结构的两种状态：h(X)≤0失效状态，h(X)>0安全状态。式(3)中各随机参数相互独立，均值矩阵和方差矩阵为矩阵μ=(μ1，μ2，…,μN)、D=(D1，D2，…,DN),则有：

(4)

可靠性指标定义为：

(5)

式中：β—联系系数；

μg—状态函数的均值；

Dg—状态函数的方差；

若h(X)服从正态分布，可以得到可靠度

R=φ(β)

(6)

式中：φ(β)—标准正态分布函数。

利用Monte Carlo模拟理论计算主轴可靠度，可靠度对基本随机参数矢量的均值矩阵μ和方差矩阵D的灵敏度为：

(7)

式中：

(8)

考虑到机床主轴所受的最大应力，如表2所示，进行了主轴可靠性分析的实例分析计算。计算步骤和方法如下。

表2 主轴试验测得的最大应力值

3 核电轮槽铣床主轴的概率有限元可靠性分析

利用ANSYS的概率有限元设计模块PDS对核电轮槽铣床主轴进行可靠性分析时，基本流程如图2所示[7-10]。主要分为以下三个步骤：首先生成分析文件，其次进入可靠性分析阶段，再次对分析结果进行后处理。

图2 PDS计算流程

(1)生成分析文件。分析文件是可靠性分析中至关重要的一环，文件需用APDL语言编写，包括预处理、求解模块、结果提取等内容。结构分析程序通过重复执行分析文件来完成可靠性分析的循环。所有影响结构行为的不确定因素(主轴前端直径、弹性模量、扭矩)对应的参数均被指定为输入变量，随机参数表见表3。对应于分析的结构行为(最大应力或最大变形等)参数被制定为输出结果。

表3 随机参数表

(2)可靠性分析阶段。该阶段主要包括：进入可靠性分析文件；选择定义输入变量以及输入变量之间的相关系数，确定个输入变量服从的分布类型、分布函数及其参数；指定输出结果变量；选择分析工具和方法；执行可靠性循环。

(3)结果后处理。可进行抽样过程显示、绘制设计变量的柱状图、绘制失效概率分布函数、确定结构可靠性分析中输入、输出变量之间的相关系数矩阵以及灵敏度分析。

通过以上所述，根据主轴刚度的失效准则，轮槽铣床的最大变形量不容许超过许用变形量，则极限状态函数定义为[11]：

Z(x)=[L]-lmax

(9)

如果Z(x)>0，系统安全，否则失效。这里设定[L]=0.12mm，采用蒙特卡罗法，抽样500次，经过计算可以得到Z的采样值。利用概率有限元法对核电轮槽铣床主轴的可靠性分析结果如图3、4、5、6所示，其中得到3个参数的概率分布函数如图3、4、5所示。

图3 直径的概率分布函数 图4 扭矩的概率分布函数

图5 弹性模量的概率分布函数 图6 输出结果Z的采样值

分别计算得到弹性模量，直径，扭矩的直方图，它可以检验循环次数是否足够。从直方图7、8、9、10可以看出，曲线光滑，抽样足够。

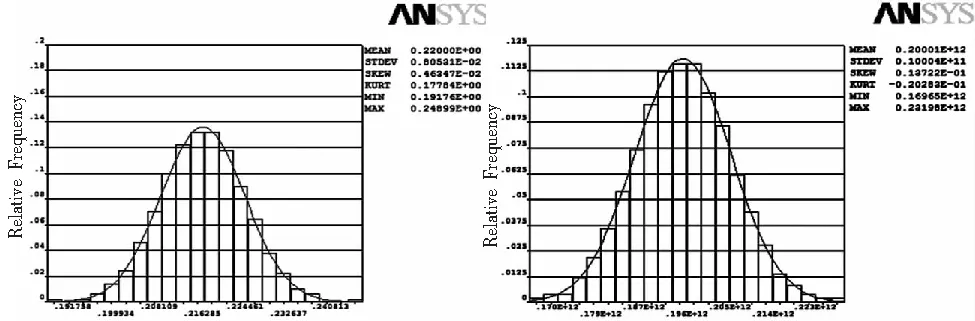
图7 直径的直方图 图8 弹性模量的直方图

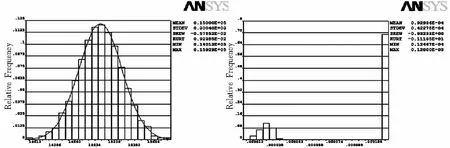
图9 扭矩的直方图 图10 输出结果Z的统计直方图

对于蒙特卡罗法，设置置信概率为95%的情况下，得到三个参数变量和输出结果的累积分布曲线如图11、12、13、14所示。

图11 直径的累积分布曲线 图12 弹性模量的累积分布曲线

图13 扭矩的累积分布曲线 图14 输出结果的累积分布曲线

通过上面的分析，可以得到扭矩，直径，弹性模量对主轴变形的影响主次关系，从而获得他们的灵敏度。

图15 各参数的灵敏度分布图

4 结论

从图15中可以看出，相对于以上三个因素中，主要影响主轴变形的因素是直径，占比62%，其次为弹性模量，最后是扭矩，其中扭矩对主轴的变形影响相对于这三个因素，非常小，这主要原因在于判断扭矩的变化范围上偏小。最后得到在置信水平为95%情况下，从输出结果Z的采样值可以看出主轴的可靠性大小为100%，采样的值均大于零，说明都是合格的。

[1]李宏胜.数控机床闭环进给伺服系统运动误差的研究[J].机床与液压, 2007, 35(2):69-72.

[2]李宏胜,孙权,张建华,等. 基于前馈控制的数控机床进给运动轮廓误差分析[J]. 组合机床与自动化加工技术,2010(2):9-11,15.

[3]李宏胜.数控机床轮廓运动精度的分析与研究[J].机械制造, 2002(10): 10-12.

[4]孙志礼,陈良玉.实用机械可靠性设计理论与方法[M].北京:科学出版社,2003.

[5]文方针.基于有限元概率设计的结构敏感性分析研究[J].华东交通大学学报，2010,27(1):17-21.

[6] 刘永峰. 高速冲床故障及可靠性分析技术研究[D].南京：南京理工大学,2013.

[7]陈普会,肖闪闪. 飞机复合材料结构的概率设计方法[J]. 南京航空航天大学学报,2012,44(5):683-693.

[8]Liu W K.Variational approach to probabilistic finite elements·J·Eng·Mech, ASCE,1988, 114(12)∶2 115-2 131.

[9]Zhang Q, L·Pei U·Random finite element analysis for stochastical responses of structures· Computer &Structures,1997,62(4)∶611-616.

[10]Coutrears.H, “The Stochastic Finite Element Method”,Computer and Structure, 1980.12.

[11]刘北辰.工程计算力学理论与应用[M].北京：机械工业出版社,1994.

(编辑 李秀敏)

申请优先审稿须知

为振兴我国机械装备制造业，弘扬民族科学文化精神，提升期刊质量，本刊从即日起，凡是符合本刊报道范围且同时受到“国家863计划资助项目”、“国家自然科学基金资助项目”、“国家重点科技攻关资助项目”等国家级基金资助项目的原创论文，可申请优先审稿，一经录用，优先发表，欢迎业内人事、专家、学者踊跃投稿(来稿注明：“优先审稿”字样)。

注：1.本刊正常审稿时间一般为一个月，优先审稿时间为15-20天; 2.本刊正常发表文章周期为来稿后6-8个月，优先发表文章周期为5-6个月。

——本刊编辑部

Reliability Analysis of Nuclear Power Wheel Groove Milling Machine Spindle Based on Probabilistic Finite Element Method

QIN Cai-you, HUANG Juan ,LI Xiao-ru

(Department of Mechanical and Electronic Engineering，Sichuan Engineering Technical College，Deyang Sichuan 618000，China)

according to the complex factors affecting the nuclear spindle milling machine reliability, finite element analysis model of machine tool spindle was established by using the ANSYS parametric modeling and probabilistic finite element module PDS , the spindle tip diameter, the elastic modulus and the torque which affect the spindle reliability were regarded as random variables , the reliability probability finite element calculation of the spindle was carried out by using a combination of probabilistic finite element method and Monte Carlo simulation method phase. The results show that when the confidence probability is 95%, three design variables histogram, random failure probability distribution function, cumulative distribution curve and sensitivity analysis are get. The method puts forward thinking approach for the analysis and design of machine tool spindle reliability and has good application prospects.

nuclear power wheel groove milling machine spindle; probabilistic finite element; monte carlo simulation; reliability analysis

1001-2265(2014)05-0023-04

10.13462/j.cnki.mmtamt.2014.05.006

2013-11-20

覃才友(1978—)，男，四川达县人，四川工程职业技术学院工程师，硕士，主要从事机械设计制造、自动控制研究等，(E-mail)qcfri@126.com。

TH166;TG659

A