含多运动副间隙机构动态特性研究*

丁 键，赵 宇，吴洪涛，陈 柏，朱留存，谢亚非

(1.南京航空航天大学 机电学院，南京 210016；2.常州精锐自动化装备技术有限公司，江苏 常州 213032)

含多运动副间隙机构动态特性研究*

丁 键1，赵 宇1，吴洪涛1，陈 柏1，朱留存2，谢亚非2

(1.南京航空航天大学 机电学院，南京 210016；2.常州精锐自动化装备技术有限公司，江苏 常州 213032)

为了研究运动副间隙对机构动态特性的影响，文章基于一种非线性接触碰撞力模型和修正了的库仑摩擦力模型，描述含间隙运动副内关节元素的接触碰撞作用，并在动力学仿真软件ADAMS环境中，以含运动副间隙曲柄滑块机构为例，对其进行动力学仿真。分别考虑间隙尺寸、间隙位置和类型、曲柄转速以及间隙数目对机构动态特性的影响，拓展了间隙碰撞动力学建模与含间隙机构动力学仿真的研究，为机构的设计提供了重要的参考依据，有利于工程实际应用。

多运动副间隙；接触碰撞；摩擦；动态特性

0 引言

在传统的机械多体系统动力学分析中，运动副通常是被假设为理想的，然而工程实际中，运动副中的间隙是不可避免的。随着精密机械和宇航工程的发展，含间隙机构动力学成为该领域迫切需要解决的关键问题之一[1-2]。文章以曲柄滑块机构为例，从转动副、移动副间隙碰撞模型的正确描述、碰撞力的准确建模入手，在ADAMS环境中仿真运动副元素间的非线性碰撞力作用，研究间隙对机构的动力学特性的影响。

1 含间隙机构动力学建模

1.1 运动副间隙的矢量模型

理想转动关节轴和轴承的中心由旋转副连接并重合，间隙使得机构获得平面内两个径向移动自由度。如图1所示，轴和轴承未发生接触变形时，间隙矢量的大小被限制在以轴承中心为圆心，以轴承半径RB和轴半径RJ之差c为半径的间隙圆内，即：

c=RB-RJ

(1)

图1 转动副间隙示意图

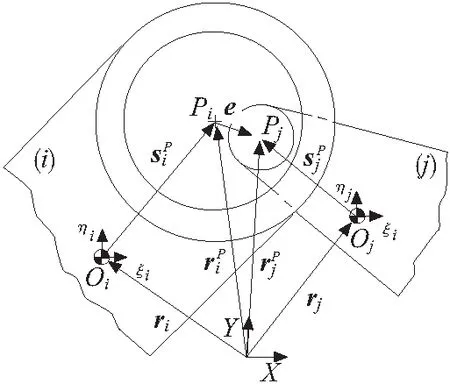
图2 转动副间隙矢量图

(2)

当轴和轴承发生接触变形时，如图3所示，由此引起的接触形变量δ为间隙矢量大小e和间隙大小c之差：

δ=e-c

(3)

图3 轴和轴承接触变形

国内外关于移动副间隙的动力学研究文献[4-6]相对较少。滑块和导轨被看成两个碰撞体，滑块在导轨内存在如图4所示的四种典型接触方式: 图4a自由飞行; 图4b滑块的一条棱边和导轨表面接触; 图4c滑块一个侧面和导轨表面接触; 图4d滑块相对棱角和导轨表面接触。

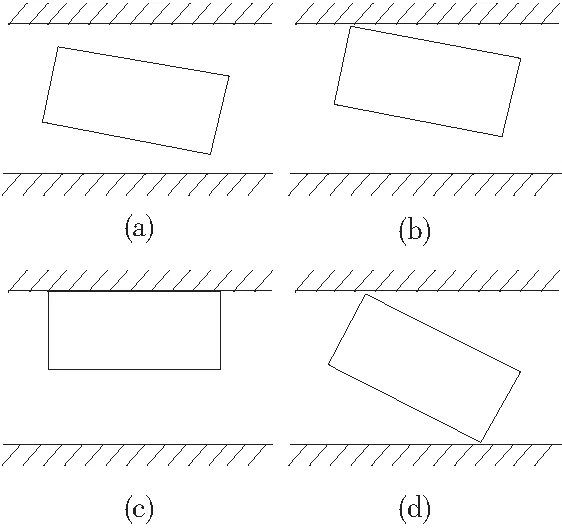
图4 滑块与导轨表面接触状态

(4)

1.2 运动副间隙的接触碰撞力模型

含间隙机构动力学分析在很大程度上取决于接触碰撞力的建模。Lankarani-Nikravesh(L-N)模型[7]在通用Hertz接触力表达式的基础上，考虑碰撞过程中由材料阻尼引起的能量损失行为，其表达式为：

(5)

(6)

其中刚度系数Kn和阻尼系数Dmod分别为：

(7)

(8)

式(7)中复合杨氏模量E*关于轴承、轴的杨氏模量EB、EJ和泊松比VB、VJ的函数关系为：

(9)

图5 移动副间隙矢量模型

移动副间隙接触力模型主要取决于滑块和导轨的接触方式。当滑块两个相邻的拐角接触导轨表面，如图4c产生面接触时的情形，Lankarani于1988年提出了该型接触碰撞中弹性力FN关于接触长度a、接触形变δ和材料固有属性σi、σj的线性模型表达式为：

(10)

当滑块产生角接触，即如图4(b)、(d)时，假设滑块拐角处有一个小的曲率半径,则接触力产生于弧面和平面之间，Goldsmith通过实验测得球体i和平面j在碰撞过程中的接触碰撞弹性力为关于球体半径Ri、材料属性σi、σj和接触形变的函数：

(11)

在这里用于近似计算滑块和导轨角接触时的接触弹性力，相应的阻尼系数可由式(8)计算得到。

1.3 运动副间隙的摩擦力模型

本文所研究机构中的摩擦不考虑润滑作用，即干摩擦。最为著名的摩擦力模型[9]是Coulomb摩擦模型，较为广泛地使用于冲击或碰撞中的摩擦行为。为了更加精准地描述物体之间的摩擦行为，以及物体相对低速情况下易发生的粘滞-微滑现象，本文采用修正[10]了的Coulomb摩擦力模型，其计算表达式为：

(12)

式(12)中动态摩擦系数μ(vt)的函数表达式为：

(13)

式中vt为切向滑动速度，μd为动摩擦系数，μs为静摩擦系数，vs为静摩擦临界速度，vd为最大动摩擦临界速度，其函数曲线如图6所示。

图6 动态摩擦系数随切向滑动速度曲线

2 含间隙机构动态特性研究

2.1 机构几何参数与质量特性

含间隙曲柄滑块机构如图7所示，曲柄-连杆转动副A处、连杆-滑块转动副B处以及滑块-导轨移动副C处可以设置间隙。机构参数如下：曲柄长度l1=50mm、质量m1=0.58kg、转动惯量J1=122.86kg·mm2；连杆长度l2=120mm、质量m2=0.94kg、转动惯量J2=141.27kg·mm2；滑块质量m3=0.98kg、转动惯量J3=245.74kg·mm2，恢复系数Ce=0.9，杨氏模量E=207GPa，泊松比ν=0.29。

图7 含间隙曲柄滑块机构

2.2 动态仿真分析

为研究运动副间隙对机构的运动特性影响，取间隙c=0.5mm，曲柄转速为ω=200rpm，进行动力学仿真，分别仅考虑机构在运动副A,B和C处存在间隙，系统稳定后的两个完整周期内，含间隙机构和理想机构的滑块运动特性曲线对比如图8～10所示。

通过上述对比结果可知，间隙对滑块的位移几乎没有影响，对滑块速度影响较小，而对滑块加速度影响最大。图8和图9表明，转动副A处间隙对滑块运动的影响相对B处间隙的影响要大，这说明间隙离曲柄越近对机构的影响越大，这与文献[11]的实验结论一致。对比图8～10发现，移动副间隙对滑块运动的影响要比转动副间隙的影响更明显，这是由于滑块在导轨内的运动状态相对轴在轴承内的运动状态较复杂导致的。

进而研究间隙尺寸对机构动力学性能的影响，以运动副B存在间隙为例，取间隙分别为0.5mm，0.2mm以及0.05mm，在同一转速200rpm下进行动力学仿真，将其动态特性曲线与理想机构作对比如图11～13所示，图中a、b、c和d分别描述系统稳定后的两个完整周期内，滑块加速度、曲柄驱动扭矩、Poincaré 映射(滑块加速度关于速度的函数曲线，其光滑程度表示系统的稳定程度)和第一个周期内间隙关节碰撞力曲线。

对比发现，间隙越小，表征系统动态特性的曲线越光滑，即系统动态特性越趋于理想机构，这与文献[11]的实验结果一致；对比图11～13中d可见，间隙的存在使得关节接触碰撞力大幅提高并且在系统稳定前呈高频振荡，间隙越小，碰撞力越小，但振荡频率越高，而系统建立稳定越快。

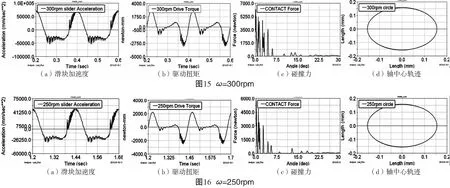
其次研究曲柄转速对含间隙机构动力学性能的影响。仍以运动副B处间隙为例，取间隙大小C=0.2mm，分别设置曲柄转速为350rpm、300rpm和250rpm对机构进行动力学仿真，结果如图14～16所示，a、b、d分别为系统稳定后两个完整周期内的滑块加速度、曲柄驱动扭矩、轴中心相对轴承参考坐标系的运动轨迹曲线，图14～16中c为系统稳定前间隙关节碰撞力曲线。

对比图14～16发现，曲柄转速越高，滑块加速度、曲柄扭矩以及碰撞力曲线振荡越厉害并且幅值越大，系统到达稳定的时间越长，图14～16中d表明系统稳定后，在没有外部冲击载荷的情况下，轴总是紧贴轴承内圈表面做圆周运动的，这些结论也都与文献[11]的实验结果相吻合。

最后，考虑机构在转动副B处和移动副C处同时存在间隙C=0.2mm，曲柄转速200rpm的情况下，对机构进行动力学仿真。取系统稳定后的两个完整周期作研究，机构动态特性参数曲线如图17所示。图17a、b分别为滑块加速度和曲柄驱动扭矩曲线，图17c、d分别为轴中心在轴承参考坐标系中和滑块中心在导轨参考坐标系中的运动轨迹曲线。

由图17a、b可见，本文研究的含多运动副间隙机构总体运行平稳，但滑块运动到上、下死点位置时，机构振动明显，表现出机构的局部混沌[12]现象，且相比只含转动副或移动副的情况要剧烈的多，显然是转动副和移动副间隙之间产生相互耦合影响。图17c、d说明随着机构的运行，间隙铰元素间可以分为三种状态：轴(滑块)沿轴承(导轨)内壁滑移、自由飞行和反弹碰撞。

3 结论

机构运行过程中，间隙不可避免地存在于各活动铰接处，并使得机构的动态特性偏离理想机构。文章基于一种非线性混合碰撞力模型和改进了的Coulomb摩擦力模型，以曲柄滑块机构为对象，在动力学仿真软件ADAMS中对其进行动态特性分析。所得结论与国外早前的实验研究结果吻合，说明了本文所采用研究方法的可行性，可用于较好地预测含间隙机构动力学行为特征，有一定的工程指导价值。

[1] Megahed, S.M., Haroun, A.F.: Analysis of the dynamic behavioral performance of mechanical systems with multi-clearance joints. J. Comput. Nonlinear Dyn. , 2011(7)：1-11.

[2] Khulief, Y.A.: Modeling of impact in multibody systems:An overview. J. Comput. Nonlinear Dyn.8, 021012 ，2013：4-7.

[3] Flores, P., Lankarani, H.M.: Dynamic response of multi-body systems with multiple clearance joints. J. Comput.Nonlinear Dyn.7(3), 031003 (2012)：2-3.

[4] Flores P, Leine R, Glocker C. Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach[J]. Multibody System Dynamics. 2010,23: 65-190.

[5] Flores P, Ambrósio J, Claro JCP, Lankarani HM. Translational Joints with Clearance in Rigid Multibody Systems[J]. Journal of Computational and Nonlinear Dynamics. 2008(3):1-10.

[6] Muvengei, O., Kihiu, J., Ikua, B.: Dynamic analysis of multi-body mechanical systems with imperfect kinematic joints: a literature survey and review. Sustain. Res. Innov.Proc., 2011(3)：61-76.

[7] Lankarani HM, Nikravesh PE. A Cont act Force Model With Hysteresis Damping for Impact Analysis of Multibody Systems[J]. Journal of Mechanical Design.1990,112:369-376.

[8] 白争锋.考虑铰间间隙的机构动力学特性研究[D].哈尔滨：哈尔滨工业大学，2011.

[9] 温诗铸，黄平. 摩擦学原理( 第3 版)[M].北京：清华大学出版社，2008.

[10] MSC Software, M.Sc. ADAMS?, Release R3, Help System(2008).

[11] Flores P. Dynamic Analysis of Mechanical Systems with Imperfect Kinematic Joints[D]. Portugal: Universidade Do Minho Ph.D thesis, 2004：185-204.

[12] 胡海岩.分段线性系统动力学的非光滑分析[J]. 力学学报，1996,28(4)：483-488.

(编辑 李秀敏)

Dynamic Characteristics of Mechanisms with Multi-clearance Joints

DING Jian1,ZHAO Yu1,WU Hong-tao1, CHEN bai1,ZHU Liu-cun2, XIE Ya-fei2

(1. College of Mechatronics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China；2. Changzhou Jingrui Automatic Equipment and Technology Co. , Ltd , Changzhou Jiangsu 213032, China)

In order to study the dynamic characteristics of mechanisms with joint clearance, the work based on a nonlinear contact model and an improved Coulomb friction model. In the environment of dynamics simulation software ADAMS, the slider-crank mechanism is chosen as an example to be demonstrated. Consider the influence of dynamic performance due to clearance size, clearance type and clearance position, rotation speed of crank and clearance numbers respectively, which expands the dynamics modeling of mechanism with clearance, and gives the basis of mechanism design.

multi-clearance joints; contact; friction; dynamic characteristic

1001-2265(2014)05-0009-05

10.13462/j.cnki.mmtamt.2014.05.003

2013-09-10;

2013-09-25

国家自然基金(51375230)；江苏省科技支撑计划(BE2012052)

丁键(1987—)，男，江苏盐城人，南京航空航天大学硕士研究生，研究方向为多体系统，(E-mail)nuaa_ding@163.com。

TH112；TG65

A