基于模态滤波的板壳类结构空间均方振速估算方法

刘监波，吴崇健，陈乐佳，陈志刚

1中国舰船研究设计中心，湖北武汉430064 2中国舰船研究设计中心船舶振动噪声重点实验室，湖北武汉430064

基于模态滤波的板壳类结构空间均方振速估算方法

刘监波1，吴崇健2，陈乐佳2，陈志刚2

1中国舰船研究设计中心，湖北武汉430064 2中国舰船研究设计中心船舶振动噪声重点实验室，湖北武汉430064

针对船舶、航空航天等工程领域中板、壳类结构振动噪声评价问题，将广泛应用于控制工程中的模态滤波理论引入到结构振动评估领域，建立了一种估算结构空间均方振速的新方法。该方法的特点是能在激励源信息未知的情况下，以布置在结构表面有限个振动传感器测量得到的振动响应作为主要输入，估算板、壳类结构的空间均方振速，从而评价结构的整体振动状态。依据该方法对一矩形平板结构受点力、线力和面力等3种典型的激励源作用下，通过少量结构振动测点的振动信息，分别对其空间均方振速进行了数值验证；同时利用一水下加肋圆柱壳结构进行了试验验证。数值和模型试验验证结果表明：利用该方法评估得到的振动速度谱线特征与精确解和实测值基本一致，评估误差在2 dB以内，满足工程应用精度要求。该方法可以应用于工程中板、壳类结构振动噪声评价和振动状态的在线监测评估。

模态滤波；模态坐标；空间均方振速；结构振动

0 引言

近年来，振动工程界越来越重视对结构振动与噪声的实时在线监测［1］，从而评价结构的振动量级并判断其是否处于正常工作状态。对于大量采用板、壳类结构的结构物（如水面船舶、水下航行器等），主要关心其法向振动量级的大小，可以采用法向空间均方振速作为其振动量级的评价指标。空间均方振速具有能量的性质，反映了结构振动的整体情况。一般来说，可以通过实时测量作用在结构上的激励力的大小，通过有限元计算或传递函数法得到其空间均方振速。但对于大型结构，特别是船舶、航空器等，其外部激励源包括机械设备、管路系统以及外部的流体，激励源性质多样，成因复杂，要在工程中准确获取十分困难，导致在掌握了频响函数以及模态参数后，结构的整体振动响应仍然无法准确知悉。因此，在激励源信息未知的情况下，在结构上合理地布置一定数量的传感器，通过测点处的振动信息（如振动加速度、振动速度或振动位移等）来重构整个结构的振动响应，得到结构的空间均方振速，评价结构的振动整体水平具有重要的工程意义，这也一直是结构振动状态评估研究领域的难点和热点问题。

陈乐佳［2］针对主要受点力作用的圆柱壳结构，从线性系统传递函数的基本理论出发，在激励源位置、数量已知的情况下，推导了有限测点振动至全结构域低频振动的传递关系，建立了基于振动测量的圆柱壳结构低频振动评价方法。陈美霞等［3］在此基础上，利用统计能量基本理论将该方法应用频段推广到了中高频段。金广文等［4-5］通过对频响函数矩阵求逆，得到了结构振动之间的传递关系，从而通过部分结构振动的振动信息重构整个结构的振动。

Bobrovnitskii［6］将结构边界分为可测区和不可测区，假定所有激励力都作用在不可测区，所用传感器都布置在可测区；将激励力作为未知量，测量得到的振动响应作为输入，求解第一类Fredholm积分方程得到整个结构的振动响应。该方法要求传感器的个数大于或等于激励力的个数才能保证解的唯一性。

模态滤波方法最早应用于消除控制工程中的观测溢出，其基本思想是利用模态的正交性，从物理坐标下的响应中提取出模态坐标的响应。Meirovitch等［7］定义了分布参数系统的模态滤波器，根据该定义构造模态滤波器时，需要知道结构的质量分布函数，这在一定程度上限制了它的应用。Zhang等［8-9］提出了一种利用实验所得的频响函数获取模态滤波器的方法，与Meirovitch提出的方法相比，该方法更接近于工程实际。Shelly［10］采用模态滤波方法从一钢质框架结构的响应中提取出了模态坐标，并讨论了不同的传感器布置对模态滤波结果的影响。传感器的布置位置对模态滤波的准确性影响较大。Kammer［11］对此开展了大量的研究工作，建立了有效独立法（Effective Independence，EfI），利用Fisher矩阵使感兴趣的模态向量尽可能地线性无关，从而最大限度地从振动响应中提取出模态信息。

本文将控制工程中应用的模态滤波理论引入到结构振动评估领域，提出一种在激励源信息未知的情况下，利用有限个测点的振动信息，估算板、壳类结构空间均方振速的新方法。该方法根据结构的频响函数以及模态参数构造模态滤波器；从有限个测点响应中提取出各阶模态坐标，通过坐标变换得到物理坐标下的响应，从而得到结构的空间均方振速值，用于评价结构的振动整体水平。该方法具有一定的工程实用价值，可以应用于工程中板、壳类结构振动噪声评价和振动状态的在线监测评估。

1 基本理论

1.1 模态滤波器构造的方法

设Φ为模态矩阵，Φr为第r阶模态向量法向分量，从中提取出对应传感器位置处的分量形成缩减模态向量φr，设ϕr为第r阶模态滤波向量，则有［8］

式中，

在p点激励（可以任意选取）时，结构的位移频响函数可以表示为

式中：ω为激励圆频率；φi为从Φi中对应传感器位置提取出的缩减模态向量；φpi为Φi中第p个分量；mi为第i阶模态质量；ωi，ξi分别为第 i阶模态圆频率和模态阻尼比；TP为模态截断数；Hp为 Nc×1的向量，其中 Nc为传感器个数；j为虚数单位。若假设Φi为质量归一化的振形，则mi=1。将式（2）的左右两边分别乘以，利用式（1），有

式（3）可写为

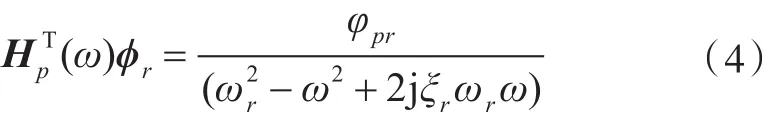
从式（4）中可以看出，模态滤波向量与结构的模态参数、模态向量、任意点至测点的频响函数及传感器的个数有关。在结构一定的条件下，模态参数、模态向量及频响函数可由理论计算或实验测量得到。文献［9］中指出，为了能够正确地实现模态滤波，传感器的个数Nc必须大于或等于分析频段（ωA≤ω≤ωB）内的结构模态数目Nf。为了求出模态滤波向量，在ωA≤ω≤ωB频段内取一系列频率点代入式（4）中即可得到式（5）。一般情况下，选取的频率点越多，得到的模态滤波向量的精度越高。数值计算结果表明，在每个固有频率附近取3个频率点就可满足精度要求。

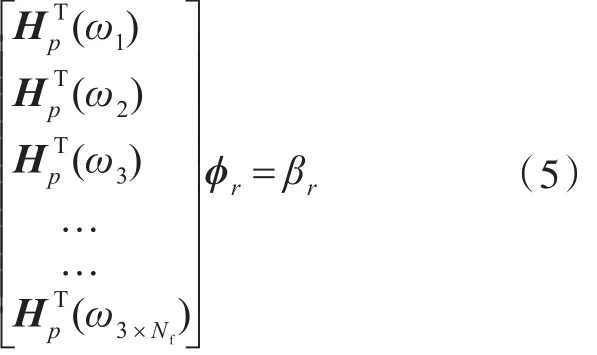
式中，

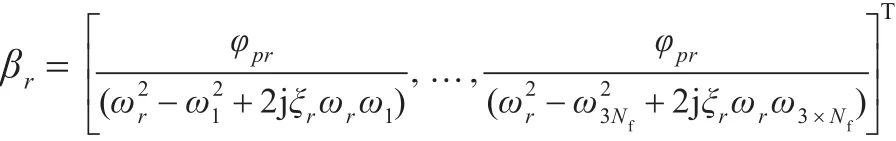
式（5）为一个超定方程，采用最小二乘法求解其最佳逼近解：

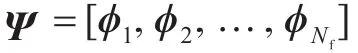
在实际工程中求模态滤波向量时，可以任意选取一个激励点（不一定是真实的激励源位置）进行激励，得到激励点到测点的频响函数。将测量得到的频响函数、模态参数及模态向量代入式（5）、式（6）得到模态滤波向量。

1.2 传感器数和位置的选取方法

文献［9］的研究表明，要准确获取模态坐标，布置在结构上的传感器个数Nc必须大于或等于频段内的模态数目。在工程实际中，由于评估的频带较宽，且模态较为丰富，在整个评估频段内很难满足传感器数Nc大于模态数的条件。本文在文献［9］的基础上，提出一种分频段的模态坐标提取方法，通过将分析频段划分为若干个子区间，使布置的传感器数等于或大于子区间内的结构模态数目，以确保模态滤波的准确性，同时还可降低传感器的数量，使方法更具通用性。传感器数Nc由式（7）确定。首先根据分析频段带宽和结构模态的密集程度选取子区间数K，从而确定传感器数。

式中：Nf为分析频段ωA≤ω≤ωB内总模态数；K为子区间数；「」为向上取整。

传感器的布置位置对模态滤波的精度有显著影响。当传感器数量确定后，布置位置可以采取Kammer建立的有效独立法（EfI）从众多备选位置中逐步缩减获取。具体方法如下：

定义候选测点群（数量大于Nc）对模态矩阵线性无关的贡献矩阵

式中，A=[φ1，φ2，…，φr]，为按照候选测点缩减后的模态矩阵。

A为幂等矩阵（A2=A），其对角线上元素Aii反映了第i个测点对缩减模态线性无关性的贡献度，满足0≤Aii≤1。若Aii=0，表示在第i个测点上无法识别关心的模态；若Aii=1，表示第i个测点为关键测点。对Aii大小排序，删除Aii最小值代表的测点。对剩余测点重新生成并计算A矩阵，进行循环迭代缩减，直至达到设定的传感器数Nc。

1.3 模态坐标的提取

当结构振动频率ω属于第s（s=1～K）个子区间时（即 ωAs≤ ω ≤ ωBs，ω ，ωAs，ωBs分别为结构的振动圆频率、第s个子区间的下限圆频率和第s个子区间的上限圆频率，不同的区间频率宽度不同），认为该子区间内的模态对振动响应有主要贡献，忽略该子区间外模态的贡献。则任意激励力作用下测点处的响应向量x（ω）可表示为

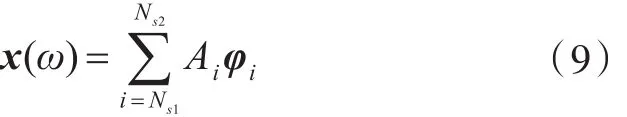
式中：F（Q）为载荷分布函数；＜，＞表示内积。

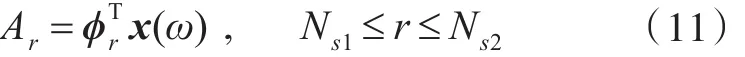
结构的位移响应向量为

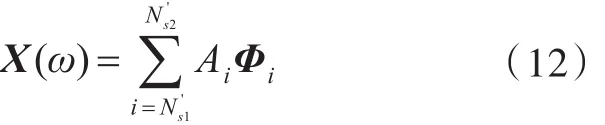
1.4 板壳类结构空间均方振速估算

本文主要考虑板、壳体类结构的空间均方振速的估算，其空间均方振速的定义为

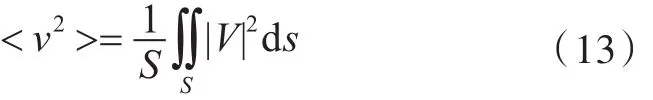
式中：S表示振动面的面积；V为振动面的法向振速度分布函数。

将式（11）代入式（12），可得结构振动的空间均方速度为

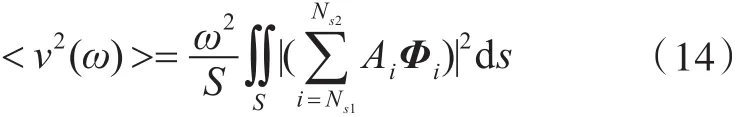
式中，ωAs≤ω≤ωBs。

将式（10）代入式（13），可得模态滤波向量和结构空间均方振速的关系：

式中，Δs为单个离散节点所代表的面积。

将空间均方振速写作空间均方振速级为

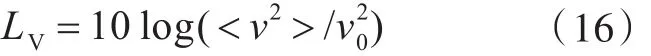
式中，v0=1×10-9m/s。

将各个频点的振动量级采用能量叠加的方式得到振动总级

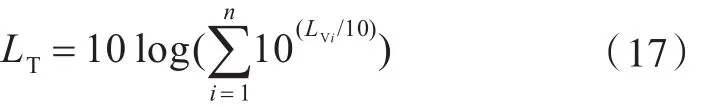
式中：LT为振动速度总级；Lvi为第i个频点的振动速度级；n为分析频段内参与总级计算的频点数。

2 数值分析

2.1 矩形板主要参数

本文以一四边简支的矩形薄平板为例来进行说明，如图1所示。该平板宽度a=1.1 m，长度b=2.3 m，厚度 t=12 mm；材料参数为：弹性模量E=210 GPa，泊松比 μ =0.3，阻尼比取 ζ=0.05。

2.2 传感器数目及位置

若分析频段为10～300 Hz，经计算，该频段内共有15个模态，可将频段分为3个子区间（K=3）。根据式（7），传感器数选取为5个。按照有效独立法，确定了5个加速度传感器的布置位置分别 为 ：（0.75，1.75），（0.75，1.25），（0.77，0.72），（0.34，1.22），（0.73，1.64）。

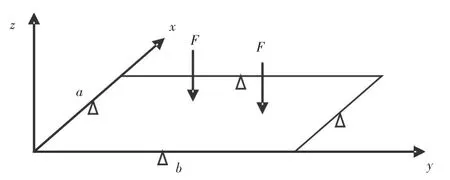
图1 四边简支矩形钢板Fig.1 Schematic view of the supported steel plate

2.3 矩形板模态坐标的提取

对每个子区间采用本文方法分别求出其对应的模态滤波矩阵。为了说明采用模态滤波提取模态坐标的效果，以一垂直于板面、幅值为1 N的点力在（0.2，0.7）处进行简谐激励，计算出各传感器位置处的响应。采用式（11）可以从传感器测量值中提取出每阶模态坐标。图2和图3分别表示通过模态滤波方法得到的第1阶和第3阶模态坐标与精确值的对比。由图中可知，除在120 Hz附近处外，模态滤波的结果与精确解符合得较好。这是由于布置了5个传感器，模态滤波能较准确地提取模态坐标的频率范围为10 Hz～第5阶模态频率；由于该结构的第6阶模态频率为120.2 Hz，所以在120 Hz附近模态滤波结果与精确解有一定的差别。

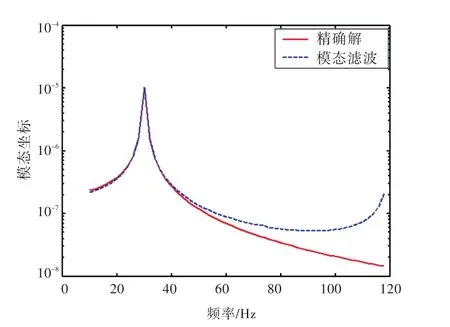
图2 第1阶模态坐标Fig.2 Mode coordinate of the first set

图3 第3阶模态坐标Fig.3 Mode coordinate of the third set

2.4 矩形板空间均方振速的估算

本文提出的估算方法不需要事先知道激励源的信息，为了说明本方法对任意的激励源都是可行的，考虑了3种不同形式（点力、面力、线力）激励源作用下的空间均方振速的估算。为便于比较，同时计算出了3种激励形式下的空间均方速度的精确解。

1）若矩形板受到2个点力的作用，作用点坐标分别为（0.2，0.7），（0.5，1.3），幅值分别为 15 N和10 N，激励频率为10～300 Hz，可以计算得到传感器位置处的响应。将其作为传感器的测量值，采用本文方法估算出矩形板的空间均方振速与精确解对比如图4所示。

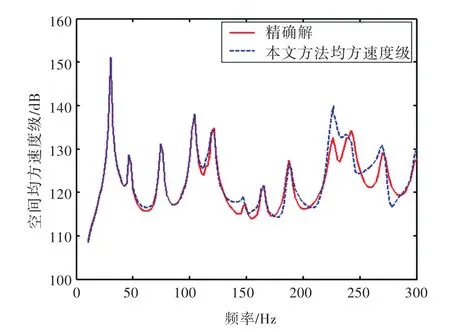
图4 矩形板空间均方振速（点力作用下）Fig.4 Spatial quadratic velocities of plate（excited by point forces）

2）若矩形板受到均匀面力的作用，作用范围为 0≤x≤a/2，0≤y≤b/2，面力的幅值为 10 N/m2，激励频率为10～300 Hz，得到的均方速度级与精确解的对比如图5所示。

3）若矩形板受到均匀线力的作用，作用位置为x=0.5 m，0≤y≤b/3，线力的幅值为10 N/m，激励频率为10～300 Hz，得到的均方速度级与精确解的对比如图6所示。

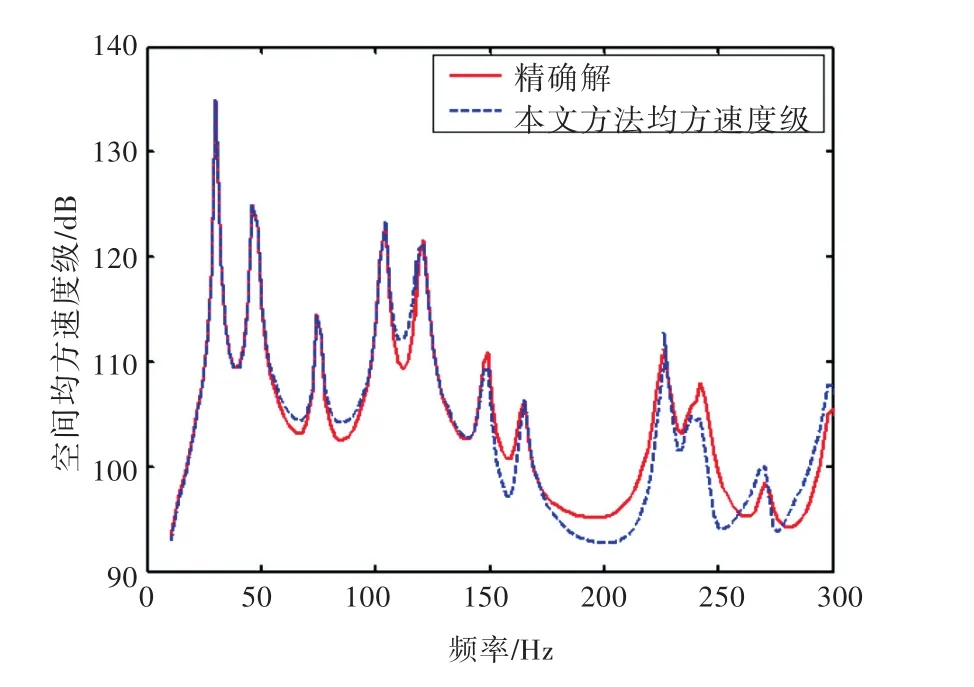
图5 矩形板空间均方振速（面力作用下）Fig.5 Spatial quadratic velocities of plate（excited by surface forces）

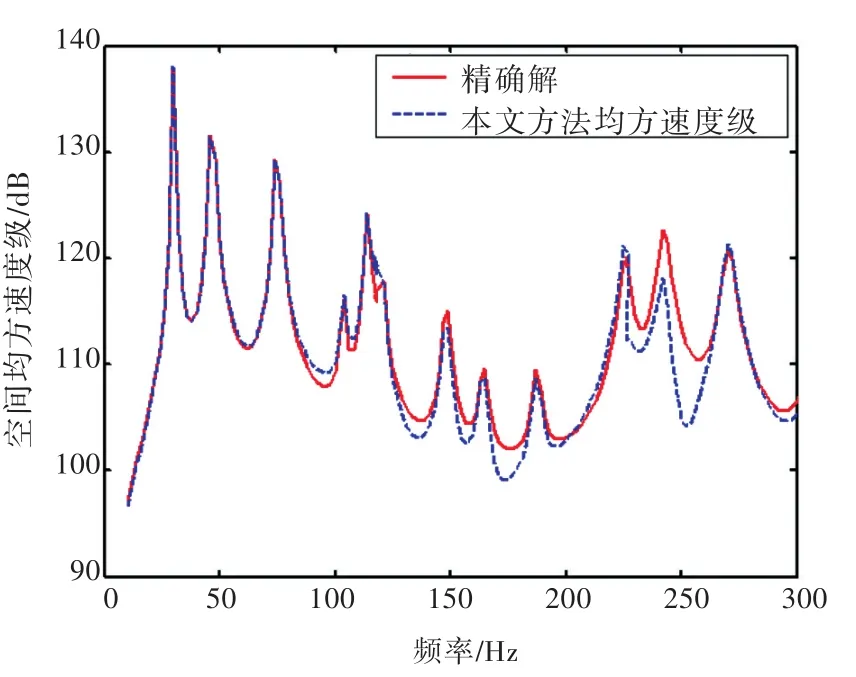
图6 矩形板空间均方振速（线力作用下）Fig.6 Spatial quadratic velocities of plate（excited by line forces）

从图4～图6中可以看出，在本文所考虑的3种形式的激励源作用下，估算得到的均方速度级与精确解的误差较小，说明该方法能通过测量得到的振动响应来较准确地估算空间均方振速。从图中还可以看出，估算值在峰值附近与精确值符合性较好，在谷值附近有一定的误差，分析认为这是由于本文只考虑了结构的共振响应而忽略了非共振响应，在峰值附近共振模态起主要作用，所以估算值与精确值基本重合。而对于谷值位置而言，共振模态和非共振模态对振动响应的贡献相差不大，所以在谷值位置，估算值和精确值有一定的差别，但并不影响对结构振动状态的整体性评价。从表1给出的估算值与精确解的空间均方振速总级对比来看，两者相差约1 dB，表明本方法对评价结构的整体性振动具有较高的精度。

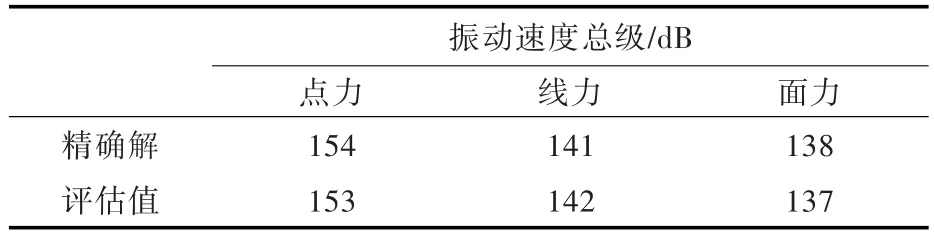
表1 空间均方振速总级对比（10～300 Hz）Tab.1 Comparison of the total level of spatial quadratic velocities

3 模型试验验证

为进一步验证本文建立方法的实用性，利用一水下加肋圆柱壳进行了模型试验验证。加肋圆柱壳结构如图7所示。加肋圆柱壳内部用一激振机激励，激励力大小未知。壳体内部共布置加速度传感器18个，用于获取激振机激励作用下壳体结构的振动响应。

通过有效独立法，从18个传感器中选取出其中的3个作为输入。按照本文方法进行空间均方振速的评估。作为评估值的对比，将18个测点的振动加速度转化为振动速度并计算平均值，称之为实测值。

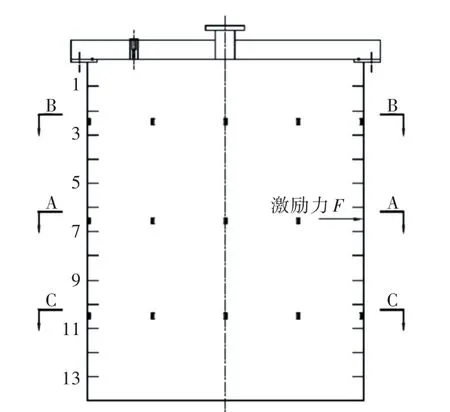
图7 加肋圆柱壳试验模型Fig.7 Ring stiffened cylindrical shell

表2给出了本文方法给出的空间均方振速总级评估值与实测值的对比，两者误差为1.5 dB。图8给出了20～800 Hz频段空间均方振速评估值与实测值频谱特性的对比。对比表明，评估值与实测值频谱特性的一致性较好。

表2 空间均方振速总级对比（20～800 Hz）Tab.2 Comparison of the total level of spatial quadratic velocities between the calculation value and the test value（20～800 Hz）

图8 评估值与试验值的对比Fig.8 Comparison of spatial quadratic velocities between calculation values and test values

4 结 语

1）本文针对工程领域中板、壳类结构振动噪声评价问题，创新性地将广泛应用于控制工程中的模态滤波理论引入到结构振动评估领域，采用模态参数、模态向量以及频响函数构造了对应的模态滤波器，建立了基于模态滤波的板、壳类结构空间均方振速估算方法。该方法的特点是能在激励源信息未知的情况下，以布置在结构表面有限个振动传感器测量得到的振动响应作为主要输入，估算板、壳类结构的空间均方振速，从而评价结构的整体振动噪声状态。

2）应用该方法分别估算了一矩形平板受3种不同形式激励源作用下的空间均方振速，估算得到的振动速度谱线特征与精确解基本一致，振动速度总级相差约1 dB。同时，利用一水下加肋圆柱壳进行了模型试验，验证表明评估方法给出的评估值满足工程应用的谱线特征和总振级精度要求，表明该方法具有一定的工程实用价值，可以应用于工程中板、壳类结构振动噪声评价和振动状态的在线监测评估。

［1］CARNIER B，VAUCHER DELA CROIX D，WEBSER D.From vibration monicoring to acoustic mornitoring of a ship［C］//Fifth International Congress on Sound and Vibration Adelaide South Australia， 1997：993-1000.

［2］陈乐佳.结构中低频振动与辐射噪声评估方法［D］.武汉：华中科技大学，2006.

［3］陈美霞，袁自强，汪浩，等.基于振动测量的加肋圆柱壳中高频振动预报［J］.中国舰船研究，2007，2（4）：31-36.

CHEN Meixia，YUAN Ziqiang，WANG Hao，et al.Pre⁃diction of vibration in middle-high frequency for stiff⁃ened shell based on vibration measurement［J］.Chinese Journal of Ship Research，2007，2（4）：31-36.

［4］金广文，何琳，姜荣俊.基于频响函数求逆法的双层圆柱壳体速度场重构［J］.振动与冲击，2007，26（8）：60-63.

JIN Guangwen，HE Lin，JIANG Rongjun.Reconstruc⁃tion of the velocity field for cylindrical double shells based on frequency response functions［J］.Journal of Vibration and Shock，2007，26（8）：60-63.

［5］金广文，何琳，姜荣俊.基于速度场重构的双层圆柱壳壳体振动传递特性试验研究［J］.振动与冲击，2007，26（10）：180-183.

JIN Guangwen，HE Lin，JIANG Rongjun.Vibration transmissibility of a ribbed cylindrical double-shell based on reconstructing velocity field［J］.Journal of Vi⁃bration and Shock，2007，26（10）：180-183.

［6］BOBROVNITSKII Y I.The problem of vibration field reconstruction：statement and general properties［J］.Journal of Sound and Vibration，2001，247（1）：145-163.

［7］MEIROVITCH L，BARUH H.The implementation of modal filter for control of structure［J］.Journal of Guid⁃ance，Control，and Dynamics，1985，8（6）：707-716.

［8］ZHANG Q，SHIH C Y，ALLEMANG R J.Orthogonali⁃ty criterion for experimental modal vectors［J］.Vibra⁃tion Analysis Techniques and Applications，1989，18（4）：251-258.

［9］ZHANG Q，ALLEMANG R J，BROWN D L.Modal fil⁃ter：concept and applications［C］//Proceedings of the 8th International Modal Analysis Conference.Orlando，Florida，1990：487-496.

［10］SHELLY S，ALLEMANG R J，FREUDINGER L，et al.Implementation of a modal filter on a five meter truss structure［C］//9th Conference International Mod⁃alAnalysis Conference （IMAC）.Italy， 1991：1036-1044.

［11］KAMMER D C.Sensor placement for on-orbit modal identification and correlation of large space structures［J］.Journal of Guidance，Control，and Dynamics，1991，14（2）：251-259.

Estimation of the Spatial Quadratic Velocity ofShells and Plate Structures Based on a Modal Filter

LIU Jianbo1，WU Chongjian2，CHEN Lejia2，CHEN Zhigang2

1 China Ship Development and Design Center，Wuhan 430064，China 2 National Key Laboratory on Ship Vibration and Noise，China Ship Development and Design Center，Wuhan 430064，China

Aiming at structural vibration assessment problems in the aerospace and ship engineerings，a new method for estimating the spatial quadratic velocity of plates and shells is presented using the theory of modal filter that has been widely used in the field of control engineering.The innate feature of the proposed method is that it can be applied in the case where the information concerning excited forces is unknown.To validate the method，the spatial quadratic velocities of a rectangle flat plate excited by three different types of forces，namely point forces，line forces，and surface forces，are estimated respectively，using the vibration information from a few measurement points.Meanwhile，various tests were carried out on an underwater ring stiffened cylindrical shell for further verification.The results show that the suggested method is precise in estimating the vibration spectrum，where the error is within 2 dB.Overall，the method can be used to estimate the spatial quadratic velocity of the structures in both actual practices and online monitoring.

modal filter；mode coordinates；spatial quadratic velocity；structural vibration

U661.44；TB123

A

1673－3185（2014）02－48－07

10.3969/j.issn.1673-3185.2014.02.009

http://www.cnki.net/kcms/doi/10.3969/j.issn.1673-3185.2014.02.009.html

期刊网址：www.ship-research.com

2013－08－27 网络出版时间：2014-3-31 16:32

国家部委基金资助项目

刘监波（1973－），男，博士生。研究方向：舰船振动与噪声控制

吴崇健（1960－），男，研究员，博士生导师。研究方向：噪声与振动控制

陈乐佳（1982－），男，博士生，工程师。研究方向：舰船振动与噪声控制。E-mail：hustclj＠163.com

陈乐佳

［责任编辑：易基圣］