基于映射声无限元法柱壳振动声辐射特性分析

田正东，苏楠，姚熊亮

1海军装备部，北京100841 2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

基于映射声无限元法柱壳振动声辐射特性分析

田正东1，苏楠2，姚熊亮2

1海军装备部，北京100841 2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

基于径向形函数可任意变阶的映射声无限元法，对加筋双层圆柱壳的振动声辐射特性进行分析。取无限长圆柱壳体为研究对象，基于映射声无限元法，通过数值计算法对其辐射声场进行研究分析；并将其数值结果与解析解进行对比分析，结果显示二者吻合较好，验证了本文方法的可行性，同时发现此方法具有计算精度好、效率高等优点。在此研究基础上，基于映射变阶声无限元法，对加筋双层圆柱壳的内壳振动特性和远场声辐射特性进行分析，分别讨论内外壳厚度、型材尺寸和托板厚度对加筋双层圆柱壳内壳体表面振动均方加速度级及远场辐射声压级的影响，其分析结果表明，内壳厚度结构参数对其内表面振动均方加速度级及远场辐射声压级的影响最明显。

加筋双层圆柱壳；映射声无限元法；结构参数；振动；声辐射

0 引 言

加筋圆柱壳体是潜艇、鱼雷及其他各种空中或水下航行器舱段的主要结构形式，而降低水下目标的振动响应和辐射噪声是水下目标声隐身技术研究的重点，因此，研究加筋圆柱壳体在流体介质中的声振特性具有重要的实际意义。根据加筋圆柱壳的振动声辐射传播机理，讨论不同结构参数对其声振特性的影响，对实际控制水下结构的噪声水平具有一定的参考价值。

在现有计算声学领域，广大学者已对加筋双层圆柱壳的振动声辐射特性进行过较深入的研究。陈越澎［1］研究了水下加筋结构受径向点激励作用的响应和声辐射，其是将加筋等效为反力和反力矩来处理；孟宪举等［2］采用圆柱壳的哈密顿原理的正则方程及其半解析法分析了加筋圆柱壳的振动特性；李小明［3］利用有限元法结合边界元法对有限长加筋圆柱壳进行了声辐射特性研究，但从有限元数据转换到边界元程序较繁琐；李学斌［4］通过能量法研究了流场中环肋柱壳的自由振动特性；刘涛等［5］采用数值/解析混合方法计算了含复杂结构的有限长圆柱壳体的声辐射。理论解析解［6］适用于求解结构几何形状较简单的振动声辐射特性，而求解复杂结构的声振特性则通常采用有限元与边界元相结合的方法，原则上，此方法可用于求解任意表面形状的水下结构的振动声辐射特性，但通过有限元+边界元法求解水下加筋双层圆柱壳体的声振特性仍存在困难。其原因在于：边界元法从理论上虽然可以求解高频声辐射问题，但在实际中难以实现，因为计算机的硬件难以承受满足边界元划分要求的精细网格。而无限元法在求解结构辐射声场问题时，其计算效率要高于边界元法。Astley等［6］根据 Burnett等［7］提出的无限元思想，重新建立了一种新的无限单元类型，在此无限单元中，将权函数确定为形函数的复数共轭形式，同时采用伽辽金加权残值法进行求解。经过此种处理后，系统单元矩阵中的不确定积分被消除，同时系统矩阵中频率与刚度矩阵相互解耦。Cremers等［8］在此基础上将Astley等提出的声学无限元法改善成为一种径向形函数，可实现任意变阶的映射声学无限元法。Laulagnet等［9］通过有限元法对加肋圆柱壳体声辐射特性进行研究，分析了外力位置及肋骨对加肋圆柱壳体声辐射特性的影响，但未给出高频段内的计算结果；商德江等［10］利用有限元与边界元相结合的方法对加肋圆柱壳体的受激振动与声辐射进行数值分析时发现，在高频段求解结构声振方程计算效率低，而且进行水下振动与声辐射测量也较困难。综上所述，现在大部分的研究都只局限于低频段，而针对高频段内复杂结构的振动声辐射性能的研究还比较少。

求解加筋双层圆柱壳的水下声振性能时，若通过径向形函数可任意变阶的声学无限元法求解，可以很好地处理在高频段内不能解决的难题，且该方法计算效率高、精度好。故本文将采用径向形函数可任意变阶的映射声学无限元法，对加筋双层圆柱壳的振动声辐射特性进行研究分析，讨论内外壳厚度、型材尺寸及托板厚度等结构参数对加筋双层圆柱壳的内壳体表面振动均方加速度级及远场辐射声压级的影响。本文的径向形函数可任意变阶的映射声学无限元法可为水下复杂结构的声学设计提供参考。

1 映射声学无限元法理论

1.1 无限域流场模拟

可将流体看作一种声学介质，即一种弹性介质，存在的压力只与体积应变有关，无剪切应力的作用，由此来模拟声的传播问题。由声学理论可知，声音在任何弹性介质中的传播其实质为振动的传播。在流体中，振动的传播会出现伸张与压缩交替运动的现象，因此声波在流体介质中的传播形式为纵波。为模拟水下结构的真实声振情况，需要建立无限大的流场模型，其原因在于声波在水中传播时衰减很慢，但建立无限大的流场来模拟真实情况这一做法显然不可行。而在有限流场域中，因有边界阻抗的存在，在有限流场域的边界上必然会有声波的反射。因此，为解决这一难题，本文将通过采用映射声学无限元法来模拟无限域流场。

映射声学无限元法是通过一包含声源的人工边界来截断无限域流场，在人工边界以内采用有限元进行离散，而在边界上则敷设一层无限单元来实现无限大流场。映射声学无限单元可以直接应用于声学有限元流场和结构的边界上，可根据实际情况减小流场模型，从而提高效率、降低成本。

流体作为一种理想的弹性介质，可将模型进行离散，求解其相关声学波动方程和运动方程［11］，进而得到流场域中声压和结构加速度。

假设流体是理想的声学介质，其在流场域内满足以下声学波动方程：

式中：k=w/c，为声学波数；Δ2为拉普拉斯算子。

1.2 映射函数

本文基于径向形函数可任意变阶的映射声学无限元法，从两个方向上独立构造形函数。在径向方向上，采用任意阶数的拉格朗日多项式实现径向形函数的任意变阶；在横向方向上，保持其形函数不变，以便于与低阶有限单元耦合。

为求解声学波动方程及相应的边值问题，引入了较为简单的人工边界，将无限域流场划分为内部和外部两个区域。在内部区域使用有限元进行离散；在外部区域采用映射声学无限单元离散，无限单元为向无限远扩展的四节点单元，如图1所示。此无限四节点单元由一正方形原始单元映射得到，节点A和节点B位于人工边界上，节点A，B，C，D分别与原始单元中的4个节点相对应，节点（1，1）和（1，-1）映射到无穷远处。可分别在原始单元中的AC和BD两个方向上等间距地插入(n-2)个节点，而反映到实际单元中的节点是非等间距的。n阶声学无限元在径向方向至少需要n+1个高斯积分点，在横向方向至少需要3个高斯积分点。变阶无限元中沿半径发散方向的径向形函数与有限长方向上的横向形函数是相互独立构造的。在母单元中，在径向方向上采用拉格朗日多项式作为插值函数，这样就可以在径向无限元单元上实现任意的变阶。节点C′，D′与节点C，D关于节点A，B镜像。从原始单元中的局部坐标系η-φ到全局坐标系x-y的映射函数为：

其中，

图1 声学映射单元Fig.1 Acoustic mapped element

沿着边AC和边BD的几何映射关系式可以表示为

式中：r为沿AC或BD边距声源点C′或 D′测得的距离。

2 映射声无限元有效性验证

本文基于径向形函数可任意变阶的映射声学无限元法，以一浸没在无限流场域中的无限长圆柱体为研究对象，通过Matlab编程来求解无限流场域中的声压，并将其结果与文献［12］的解析解进行对比。在此数值计算中，取声学介质密度ρ =1 000 kg/m3，声传播速度 c=1 500 m/s。

取无量纲化参数ka=π(a=1 m)，偶极子置于无限长圆柱体的几何中心，偶极子声辐射在声场中的声压幅值等值线如图2所示。选定声学波数k，使圆柱壳体直径2a对应一个波长，在此算例中，取法向速度边界条件V0=1 m/s。

图2 偶极子声辐射数值解与解析解对比Fig.2 Comparison of numerical solution and analytical solution of dipole sound radiation

3 基于映射声无限元法的加筋双层圆柱壳体声振特性分析

3.1 模型参数

本文的计算结构模型为有限长加筋双层圆柱壳，该模型壳体内表面(L/2，0)处受径向激励力作用，取计算频段范围为100～400 Hz。其中，结构材料属性为：杨氏模量 2.1×1011N/m2，泊松比 0.3，密度7 800 kg/m3；流体材料属性为：声速1 500 m/s，密度1 000 kg/m3。在下文中，若不作特殊说明，这些参数均保持不变。

双层圆柱壳的几何参数为：壳体长度L=4 m，外壳半径 R=1.15 m，内壳半径 r=0.875 m，肋骨间距 l=0.3 m，托板厚度 h=0.01 m。采用球形流场模拟无限大流场，无限大流场的半径取为100 m。取远场100 m处270°方向为远场辐射声压的研究对象。为了控制在横向方向上的离散化误差，必须满足一个波长内6个节点的要求。对于中、高频段的远场辐射声压的求解，所求的频率越高，所需的结构网格划分数目就越多，波包络声学无限元法可以高效率求解中、高频段内结构外声场的远场声压，但本文仅以中频段100～400 Hz为例来阐述映射声学无限元法的应用。双层圆柱壳间采用托板连接的方式，内壳内表面等间距布置方钢环肋，托板间距为2个肋距，双层圆柱壳两端布置尾封板。加筋双层圆柱壳体结构模型示意图及有限元模型如图3和图4所示。

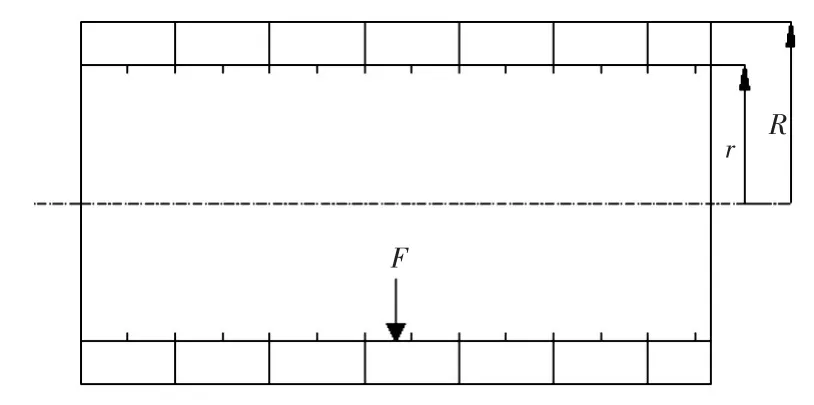
图3 加筋双层圆柱壳体结构模型示意图Fig.3 Structure model of double cylindrical shell

图4 加筋双层圆柱壳有限元模型示意图Fig.4 Finite element model of double cylindrical shell

本文通过采用映射声学无限元法给出内壳体表面振动均方加速度级及远场辐射声压级随频率变化的曲线。其中，声压级和振动均方加速度级的基准值分别为1×10-6Pa和1×10-9m/s2。

3.2 加筋双层圆柱壳结构参数对其声振特性的影响

3.2.1 外壳厚度变化对振动声辐射的影响

图5分析了外壳厚度变化对加筋双层圆柱壳体声振特性的影响。由图5（a）所示的内壳表面振动均方加速度曲线的变化趋势来看，增加外壳厚度可提高系统刚度，改变加筋双层圆柱壳的振动特性，使曲线的第1个共振峰稍微右移，在250 Hz以上频段，振动均方加速度级的降低较明显。由图5（b）所示的远场辐射声压级曲线可知，外壳厚度变化对远场辐射声压的影响较大，壳厚的增加能加大声能量的损耗。在100～400 Hz计算频段内，外壳厚度的增加使远场辐射声压均有不同程度的降低。在频点135 Hz处，外壳厚度的增加使远场辐射声压最大相差近35 dB。

图5 外层壳厚度变化对内壳振动均方加速度级和远场辐射声压级的影响Fig.5 The influence of outer-shell's thickness variation on the vibration acceleration mean square of inner-shell and far field radiation sound pressure level

3.2.2 内壳厚度变化对振动声辐射的影响

图6比较了内壳厚度变化对加筋双层圆柱壳声振特性的影响。内壳厚度使加筋双层圆柱壳的固有频率提高。从均方加速度曲线的总体来看，在高频段（300～400 Hz）内，内壳厚度的变化使内壳表面的振动均方加速度级有较大程度的减小，而在较低频段（100～300 Hz）内，3条曲线峰值交错，内壳厚度变化在一定程度范围内影响较大。经比较远场辐射声压级曲线（图6（b））可知，在较低频段100～200 Hz内，远场辐射声压对内壳厚度变化不灵敏；在200～400 Hz范围内，内壳厚度的增加使远场辐射声压级波峰的相差量值增大。总体而言，内壳厚度变化对内壳表面振动均方加速度级的影响要大于其对远场辐射声压的作用。内、外壳体厚度变化均会引起加筋双层圆柱壳的刚度变化，从而使系统的声振特性发生改变。

图6 内层壳厚度变化对内壳振动均方加速度级和远场辐射声压级的影响Fig.6 The influence of inner-shell's thickness variation on the vibration acceleration mean square of inner-shell and far field radiation sound pressure level

3.2.3 托板厚度变化对振动声辐射的影响

图7比较了托板厚度变化对结构声振特性的影响。增加托板厚度可提高系统的刚度，降低壳体的振动。在频率200 Hz以内，增加托板厚度有效抑制了内壳体表面振动均方加速度。经比较远场辐射声压级曲线（图7（b））可知，在频段100～150 Hz内，增加托板厚度从某种程度上使远场辐射声压级有减小的趋势（除个别频点）。总之，托板厚度变化对内壳体振动的作用要比对远场辐射声压的影响明显。

图7 托板厚度变化对内壳表面振动均方加速度级和远场辐射声压级的影响Fig.7 The influence of plate's thickness variation on the vibration acceleration mean square of inner-shell and far field radiation sound pressure level

3.2.4 型材（内壳环肋）尺寸变化对声振特性的影响

图8比较了型材尺寸变化对加筋双层圆柱壳体声振特性的影响。其中，第1、第2和第3种型材的尺寸为依次减小。由图8（a）可看出，增大型材尺寸使系统的总刚度增加，提高了系统固有频率，内壳表面的振动均方加速度级曲线的第1个共振峰右移。在整个频段内，型材尺寸变化在一定程度上有效降低了振动响应。经比较远场辐射声压曲线（8（b））可知，辐射声压级波峰的量值比振动均方加速度级波峰的量值要小。由此可知，型材尺寸变化对远场辐射声压的影响不明显，而对内壳体的振动响应则有着较明显的抑制作用，其对内壳表面振动均方加速度级影响较大。

图8 型材尺寸变化对内壳表面振动均方加速度级和远场辐射声压级的影响Fig.8 The influence of ring-stiffener's bar's thickness variation on the vibration acceleration mean square of inner-shell and far field radiation sound pressure level

4 结 论

本文基于映射声学无限元法对水下结构的声振特性进行了分析。取加筋双层圆柱壳体为研究对象，分析了外壳厚度、内壳厚度和型材尺寸等结构参数对声振特性的影响。采用映射声学无限元方法对加筋双层圆柱壳进行数值计算，得到以下结论：

1）采用映射声学无限元法求解水下结构的声振特性是有效的，且计算效率高、计算精度好。

3）加筋双层圆柱壳内、外壳厚度的变化会改变系统刚度，使系统的声振特性发生变化。内壳厚度的变化较明显地改变了振动均方加速级曲线及辐射声压级曲线的峰值位置，在较低频段内，其对内壳表面振动均方加速度级的影响比对远场辐射声压级的大。在不同频段范围内，不同的内壳厚度对内壳体声振特性的影响不同，且内壳厚度对内壳声振特性的影响比外壳厚度的大。

［1］陈越澎.加筋柱壳的声学设计方法研究［D］.武汉：华中理工大学，1999.

［2］孟宪举，张策，卿光辉.加筋圆柱壳的振动特性分析［J］.振动工程学报，2005，18（1）：36-40.

MENG Xianju，ZHANG Ce，QING Guanghui.Vibration characteristic analysis of stiffened cylindrical shell［J］.Journal of Vibration Engineering，2005，18（1）：36-40.

［3］李小明.加肋圆柱壳振动声辐射特性的数值计算研究［D］.大连：大连理工大学，2008.

［4］李学斌.流场中环肋圆柱壳的自由振动特性研究［J］.舰船科学技术，2005，27（增刊）：16-20.

LI Xuebin.Free vibration analysis of ring-stiffened circular cylindrical shell sub merged in fluid［J］.Ship Science and Technology，2005，27（Supp）：16-20.

［5］刘涛，汤渭霖，何世平.数值/解析混合方法计算含复杂结构的有限长圆柱壳体声辐射［J］.船舶力学，2003，7（4）：99-104.

LIU Tao，TANG Weilin，HE Shiping.Computation of sound radiation from complicated cylindrical shell by using numerical analytical matching method［J］.Journal of Ship Mechanics，2003，7（4）：99-104.

［6］ASTLEY R J，EVERSMAN W.Wave envelope elements for acoustical radiation in inhomogeneous media［J］.Computers and Structures，1988，30（4）：801-810.

［7］BURNETT D S，HOLFORD R L.Prolate and oblate spheroidal acoustic infinite elements［J］.Computer Methodsin AppliedMechanicsandEngineering，1998，158（1）：117-141.

［8］CREMERS L，FYFE K R.On the use of variable order infinite wave envelope element for acoustic radiation and scattering［J］.The Journal of the Acoustical Society of America，1995，97（4）：2028-2040.

［9］LAULAGNET B，GUYADER J L.Sound radiation by finite cylindrical ring stiffened shells［J］.Journal of Sound and Vibration，1990，138（2）：173-191.

［10］商德江，何祚镛.加肋双层圆柱壳振动声辐射数值计算分析［J］.声学学报，2001，26（3）：193-201.

SHANG Dejiang，HE Zuoyong.The numerical analysis of sound and vibradiation from a ring-stiffened cylindrical double-shell by FEM and BEM［J］.Acta Acustica，2001，26（3）：193-201.

［11］缪旭弘，钱德进，姚熊亮，等.基于ABAQUS声固耦合法的水下结构声辐射研究［J］.船舶力学，2009，13（2）：319-324.

MIAO Xuhong，QIAN Dejin，YAO Xiongliang，et al.Sound radiation of underwater structure based on coupled acoustic-structural analysis with ABAQUS［J］.Journal of Ship Mechanics，2009，13（2）：319-324.

［12］CREMERS L，FYFE K R，COYETTE J P.A variable order infinite acoustic wave envelope element［J］.Journal of Sound Vibration，1994，171（4）：483-508.

Analysis of the Acoustic-Vibration Characteristics of Cylindrical Shells Based on the Mapped Acoustic Infinite Element Method

TIAN Zhengdong1，SU Nan2，YAO Xiongliang2

1 Naval Armament Department of PLAN，Bejing 100841，China 2 School of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China

This paper adopts the mapped variable acoustic infinite element method to analyze the acoustic-vibration characteristics of stiffened double cylindrical shells.First，the sound radiation pressure of an infinitely long cylinder is obtained via numerical analysis with the mapped acoustic infinite element method.The numerical results agree well with the analytic solutions，which proves the validity and precision of the method.Based on the mapped acoustic infinite element method，the paper then analyzes the stiffened double cylindrical shell's vibration and far-field underwater noise characteristics，where the effects of the outer shell and inner shell thickness，plate thickness，ring-stiffener's dimension on the mean-square acceleration level of surface shell vibration and the influence on the far field sound pressure level of radiation are discussed.The results show that the vibration of inner-shell thickness has the greatest influence on the above mentioned parameters.

stiffened double cylindrical shell；mapped acoustic infinite element method；structural parameters；vibration；sound radiation

U661.4

A

1673－3185（2014）02－42－06

10.3969/j.issn.1673-3185.2014.02.008

http://www.cnki.net/kcms/doi/10.3969/j.issn.1673-3185.2014.02.008.html

期刊网址：www.ship-research.com

2013－09－02 网络出版时间：2014-3-31 16:32

国家自然科学基金资助项目（51209052）；黑龙江省青年科学基金资助项目（QC2011C013）；哈尔滨市科技创新人才研究专项资金项目（2011RFQXG021）；国家部委基金资助项目

田正东（1972－），男，博士，工程师。研究方向：减振降噪。E-mail：tad_532＠163.com

苏楠（1988－），女，硕士生。研究方向：结构振动与控制。E-mail：sulanlan1988＠126.com

姚熊亮（1963－），男，教授，博士生导师。研究方向：结构减振降噪。E-mail：xiongliangyao＠gmail.com

姚熊亮

［责任编辑：卢圣芳］