一种快速建立高精密三维控制场的方法
魏林金 赵青芬
(1.江西省交通设计研究院有限责任公司江西南昌 330002;2.江西省基础地理信息中心江西南昌 330002)
一种快速建立高精密三维控制场的方法
魏林金1赵青芬2
(1.江西省交通设计研究院有限责任公司江西南昌 330002;2.江西省基础地理信息中心江西南昌 330002)
高精度的三维控制场是近景摄影测量中相机检校和有关理论研究的重要基础设施。本文介绍一种能够快速、便捷的测定控制场内控制点三维坐标的新方法,经检验,其点位精度能够达到亚毫米级别,满足高精密三维控制场的精度要求。
三维控制场;摄影测量;前方交会
0 引言
近年来,随着近景摄影测量技术和计算机视觉的飞速发展,非量测相机特别是普通数码相机的使用越来越广泛,普通数码相机相对于专业量测用相机,不仅价格相对低廉,而且携带方便。但是这类相机不是专门为摄影测量设计的,其内方位元素无法直接测定,且存在较大的光学畸变差,在用于摄影测量作业前必须对其进行相机检校,而高精密的三维控制场是实施相机检校的重要基础设施。因此,笔者提出一种快速建立三维控制场的新方法,并详细论述其建立和计算过程。
1 选择测站和建立坐标系
在布设的三维控制场标志前方的适当位置选取两个稳定、坚固的地面点作为测站点A和B,并做好标志。用钢尺测量两测站(A、B)间的基线距离D0。如图1所示,建立物方空间直角坐标系D-XYZ,该坐标系以左测站仪器中心A为原点,测站A与右测站仪器中心B连线在水平面上的投影为Y坐标轴,方向向右,垂直向上方向为Z轴,X轴垂直Z-Y平面并构成左手三维空间坐标系。因此,两测站A(XA,YA,ZA)和B(XB,YB,ZB)的空间坐标分别为A(0,0,0)、B(0,D0,hAB),其中hAB是两测站(A、B)间仪器中心的高差。
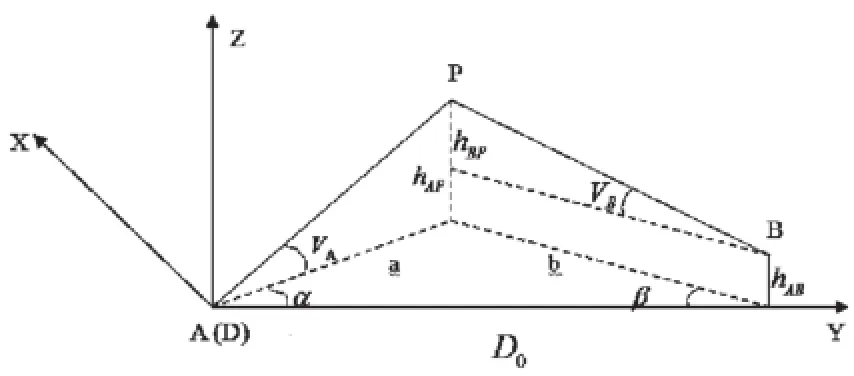
图1 三维控制场物方坐标系
2 现场观测和初步计算
2.1 现场观测
分别在测站A、B上安置高精度经纬仪或全站仪,采用方向观测法观测墙上控制点与基线AB的水平夹角α、β和相应的垂直角vA、vB,每个控制点用盘左、盘右各观测两个测回。用高精度钢卷尺精密测量墙上一些控制点间的距离,读数精确到0.1毫米。
2.2 初步计算
(1)平面坐标的确定
利用角度前方交会法解求三维控制场内每一个待定点P的平面坐标(XP,YP):

其中,α、β是由A、B测站测得P点与基线AB的夹角,(XA,YA)、(XB,YB)分别是测站A、B的平面坐标。当左测站A在坐标系原点,右测站B在坐标轴Y上,即(XA=XB=0,YA=0,YB=D0),D0为测站A、B间的基线距离,则上式可以简化为:

(2)高程的确定
利用三角高程原理,分别可得测站A的仪器中心到P点的高差hAP和测站B处的仪器中心到P点的高差hBP:

其中,vA、vB分别为从测站A、B观测P点时的垂直角,ɑ、b分别是被测点P与测站A、B之间的水平距离:
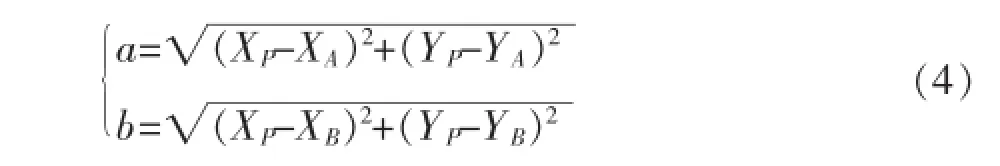
那么,AB之间的高差为:

由于P可以取控制场内三维点的任意一个点,因此可以得到N(N为待定点个数)个测站hAB,取它们的平均值作为最后测站A、B仪器中心的高差值。
由图1可知,三维控制点P点的高程ZP为:

其中,ZPA表示由测站A确定的P点的Z坐标值,等于A、P间的高差hAP,ZPB表示由测站B确定的P点的Z坐标值,等于B点的Z坐标值ZB加上B、P间的高差hBP,而ZB等于两测站A、B仪器中心间的高差hAB。
至此,得到控制场内各个控制点初步计算的三维坐标(XP,YP,ZP)。
3 严密计算
3.1 确定未知数和选择平差模型
根据平差原理,包含的未知参数有两类:一类是三维控制场内每个点的三维坐标(XP,YP,ZP);第二类是无固定观测墩引起的测站点未知数,在前面所述的物方空间坐标系D-XYZ前提下,测站未知数为B点的Y和Z坐标,即(YB,ZB)。
在现场观测中,有两类观测值:角度观测值和边长观测值。根据现场边长观测的情况,严密计算可以选择两种不同的平差模型:间接平差和附有约束条件的间接平差。当现场边长观测精度较高,相对于坐标解算的精度可以把边长观测值视作真值,从而采用附有约束条件的间接平差模型;当认为边长观测值存在较大的观测误差时,则采用间接平差模型。
3.2 列误差方程式
(1)水平角的误差方程式
由图1可得,水平角观测值的函数模型为
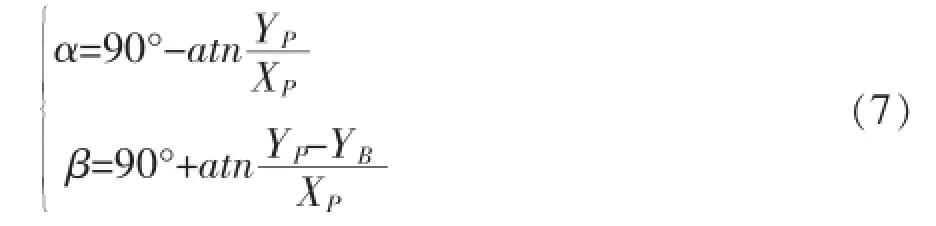
线性化处理,并代入相应的初步计算值,得到水平角观测值的误差方程式为

(2)竖直角的误差方程式
由图1可得,竖直角观测值的函数模型为

线性化处理,并代入相应的初步计算值,得到竖直角观测值的误差方程式为
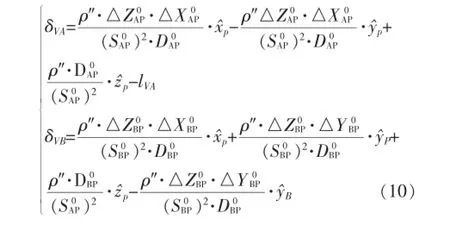
(3)观测边长的误差方程式
当把测量的控制点间的边长当作含有误差的观测值时,同样可列出边长的误差方程式。设P、Q分别为控制支架上的两个三维控制点,S为两点之间的距离,则有

线性化处理并代入相应的初步计算值,得到边长观测值的误差方程式为
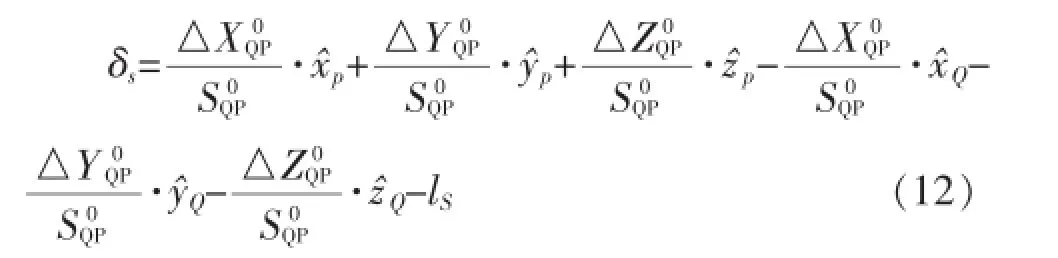
(4)约束条件式
采用附有条件的间接平差时,将精确测定的边长当作约束条件,条件式的个数等于精确测定的边长的个数。设P、Q分别为控制支架上的两个三维控制点,S为两点之间的距离,条件式为
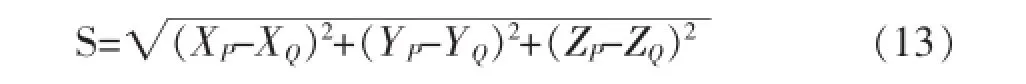
线性化后的形式为
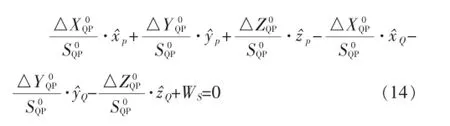
式中,WS为常数项,等于近似值减去观测值,即

3.3 最小二乘法计算
根据最小二乘法,将式(8)、式(10)和式(12)组法方程式,解法方程式求得三维控制场内个点的三维坐标(XP,YP,ZP)和未知数为B点的Y和Z坐标(YB,ZB)。
4 实例
三维控制场设计如图2所示,该控制场建立在一直角墙外侧,共设有控制标志17个,使其均匀分布于两墙表面上,点位编号如图3所示。控制标志采用不易变形的铁片标牌,其中一面刷有红、白油漆,能够长期使用而不褪色。

图2 三维控制场和控制标志

图3 三维控制场点位编号
通过现场两个测回的角度观测,取其平均值作为最后的水平观测角和竖直观测角。用钢尺测定地面测站点间的基线长度为4.8510m。测定4段控制点间的边长,如表1所示。

表1 控制点间边长观测值
笔者在VisualStudio2005编程环境下,选择间接平差模型进行编程处理。最后得到计算结果如表2所示。结果表明,控制场内控制点点位中误差全部在1.0mm以内,且误差整体均匀性较好,完全满足高精度三维控制场的精度要求。

表2 控制点计算结果
5 结束语
本文提出一种建立高精度三维控制场的新方法,其建立过程简便、快捷,不需要建立强制的对中观测墩,节省人力和物力,且经过实例论证,控制点精度能够达到毫米级,能够满足高精密三维控制场的精度要求。
[1]袁孝,佟书泉,李欣.室内三维控制场测量方法研究[J].四川测绘,2007,30(6).
[2]王留召,张建霞,王宝山.航空摄影测量数码相机检校场的建立[J].河南理工大学学报,2006,25(1).
[3]梅文胜,徐芳,陈潇.室内全景三维控制场设计与建立[J].测绘信息与工程,2011,36(6).
[4]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社.2004.

