铁熔体快速冷却过程的分子动力学模拟

周幼华，李雯慧，陶蕾，郑广

（江汉大学物理与信息工程学院，湖北武汉430056）

铁熔体快速冷却过程的分子动力学模拟

周幼华，李雯慧，陶蕾，郑广

（江汉大学物理与信息工程学院，湖北武汉430056）

利用LAMMPS建立8×8×8原子箱，采取EAM模拟大量铁原子体系。先对体系升温，让体系充分均匀，然后对体系进行不同冷却速度下的降温。经过分子动力学模拟得到能量温度曲线、径向分布函数（RDF）和体系结构。结果表明：冷却速度低于1.8×1010K/s时，结晶相变点和熔点基本重合；冷却速度超过1012K/s时，生成物为非晶；铁熔体的过冷度可达到700 K；冷却速度在1011K/s附近时，能够生成体心立方的Fe单晶。

分子动力学模拟；快速冷却；铁熔体

0 引言

对于相变温度低于熔点的晶体不能采用传统熔融提拉方法生长，因而合成单晶存在较大困难。如：传统粉末冶金法在合成的FeSi2合金时趋向于形成高温稳定的α相，很难直接得到低温稳定的β相。而采用脉冲激光沉积法，由于激光引起的微液滴是主要的传输方式，经历了快速冷却过程，直接得到β-FeSi2，而无需经过高温稳定的α相［1］。与此类似，单质铁在不同温度具有不同的晶体结构，室温下为体心立方点阵（α-Fe），晶格常数为0.286 3 nm；在912℃，α-Fe转变为具有面心立方点阵的γ-Fe，晶格常数为0.359 1 nm；温度继续升高，超过1 394℃时，将再次转变为体心立方点阵δ-Fe；δ-Fe的体心立方结构将一直保持到熔点1 538℃；在熔点以上，铁由固态转化为液态。正因为如此，传统的熔融提拉法很难获得铁单晶，通常的固态单质铁都是α-Fe和γ-Fe（或者是渗碳后的奥氏体）的混合体［2］。熔体中原子没有确定的位置，结构具有不稳定性和不确定性，熔体的团簇结构，在高速冷却时没有足够的时间形成晶体，成为非晶凝固液体系统；液相中的团簇结构，包括最近邻原子的短程有序，被保持在了非晶状态下。快速冷却过程可能会出现直接得到低温稳定相而不经过高温中间相。很多晶体的相变温度低于熔点，因而无法采用传统熔融提拉方法生长，熔体快速冷却法为这类晶体提供了一条可能的合成途径。因而对单质铁熔体快速冷却过程结晶现象的研究，有助于揭示这类单晶的生长相规律。快速凝固中并不满足稳态形核理论。实验利用快冷和深冷可使凝固的合金得到优异的性能，如扩大了固溶的极限，能使合金得到超细的晶粒度，减少偏析或者无偏析，使合金形成亚稳相。还可能生成高的点缺陷密度晶体材料，并且还可以通过快速冷却开发出准晶体、非晶体、纳米晶体等材料［3-5］。

本文采用分子动力学方法模拟铁熔体的快速冷却过程，研究冷却速度对熔体相变温度的影响。通过控制模拟过程中的起始温度（Tstart）、最终温度（Tstop）、步长（Timestep）和运行步数（Run）来控制降温的速度，得到每一步体系中分子的运动情况，计算体系能量随温度的变化，体系中分子的位置、动量、能量和最近邻原子数，由此得出铁熔体在不同冷却速度下的冷却过程中呈现的状态。

1 系统参数的计算方法

1.1 温度

在多体体系中，温度的定义采用在系统的每一个自由度上能量均分，在实际过程中，由于体系的总动能涨落，体系的瞬时温度也随之改变：

其中Nf为体系自由度，m为分子质量，v为分子速度，kB为玻尔兹曼常数，N为体系的分子数。

1.2 径向分布函数（RDF）

RDF即原子径向上的原子密度与体系总密度的比值函数。

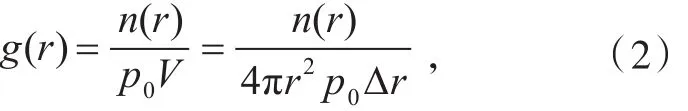
其中n(r)为半径在r到r+Δr的球壳内的原子数，p0为理想晶体的原子密度。

1.3 嵌入原子势（EAM）

EAM模型在金属系统的研究方面取得巨大成功，因为它能够很好地描述金属结合能的形成，类似于将金属的原子核嵌入自由电子气的性质。基本思想是把晶体的总势能分成两部分，一部分是在晶格点阵上的原子核之间的相互作用，另一部分是原子核在电子云中的嵌入势。

总势能为

其中Ei(pi)为嵌入势能，第二项是对势项，pi是除第i个原子以外的所有其他原子的核外电子在第i个原子处产生的电子云密度之和，

2 模拟方法

采用一个8×8×8的原子箱，用EAM来计算。分子动力学程序构成方式：

1）读入指定运算条件的参数，如初始温度、粒子数、密度、时间等。

2）体系初始化，即选定初始位置和速度。

3）计算作用于所有粒子上的力。

4）求解方程。

5）中心循环完成，计算并输出测量值。

对于过程的模拟分两步。先对体系升温，让体系充分均匀，然后对体系进行不同冷却速度下的降温。通过确定Timestep、Tstart和Tstop，可以通过控制Run来控制降温速度。

命令为

fix ID group-ID style_name keyword value...

对于style_name，采取等温等压系综（NPT）。对于keyword，包括温度标准（Tstart、Tstop、Tdamp）和压强标准（Pstart、Pstop、Pdamp）。对于温度标准，可确定Tstart和Tstop。对于压强标准，可确定Pstart和Pstop。为了使计算结果能够相对准确并且防止原子丢失，关于温度和压强的弛豫时间Tdamp和Pdamp可以采取Timestep的10～100倍。

有关Timestep（单位为ps）的选取，和原子运动时间尺度有关。一般来说，简单原子系统取10 fs；刚性分子取5 fs；软性分子，限制键长取2 fs；软性分子，无键长限制取1 fs或0.5 fs。

可以通过控制Run来确定降温速度。

采取等压等温系综（NPT），步长0.001ps，运行10 000步从1 000 K升温至2 000 K，再从2 000 K降温至200 K，运行1 000 000步，降温速度为1.8×1012K/s。

3 模拟结果与分析

3.1 铁熔体冷却过程中的相变

模拟中得到冷却速度从1.8×1012K/s到1.8× 1010K/s的冷却曲线。图1是冷却速度为1.8×1012K/s时，体系总能量和体积与温度的关系曲线。

图1所示体系总能量和体积随温度变化曲线是连续的，基本为一条直线，没有观察到明显的一级相变。因而，在此冷却速度下铁熔体会形成过冷液体——非晶态。

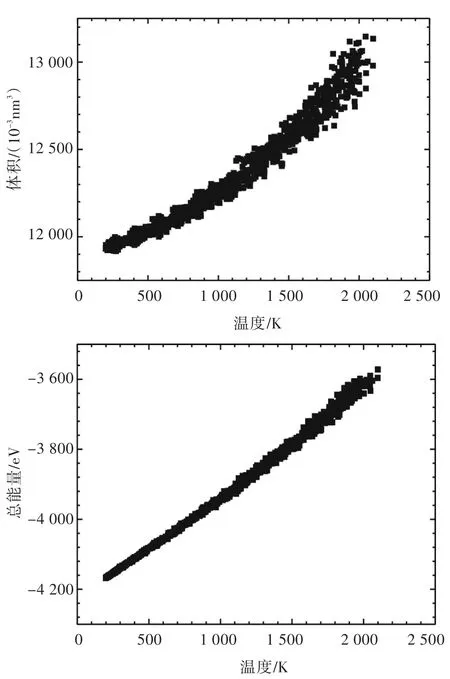
图1 冷却速度为1.8×1012K/s时，体积和总能量与温度的关系Fig.1Curve of total energy and volume vs temperature at cooling rate of 1.8×1012K/s

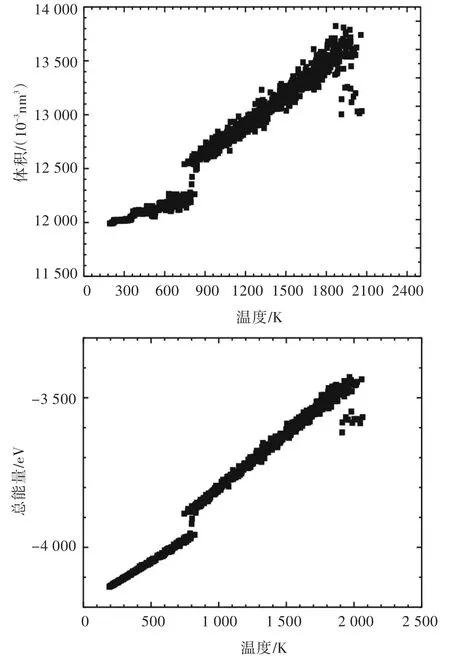
图2 冷却速度为6.5×1011K/s时，体积和总能量与温度的关系Fig.2Curve of total energy and volume vs temperature at cooling rate of 6.5×1011K/s

当冷却速度为6.5×1011K/s时，体系总能量和体积与温度的关系曲线如图2所示。能量—温度曲线总趋势为线性关系。出现了断开，意味着相变的出现。当冷却速度为6.5×1011K/s时，相变发生在800 K；当冷却速度为6.0×1011K/s时，相变发生在935 K；当冷却速度为4.5×1011K/s时，相变发生在957 K；当冷却速度为3.6×1011K/s时，相变发生在1 079 K；当冷却速度为1.8×1011K/s时，相变发生在1 057 K；当冷却速度为1.2× 1011K/s时，相变发生在1 109 K；当冷却速度为9×1010K/s时，相变发生在1 229 K；当冷却速度为7.2×1010K/s时，相变发生在1 405 K；当冷却速度为6×1010K/s时，相变发生在1 519 K；当冷却速度为3.6×1010K/s时，相变发生在1 718 K；当冷却速度为1.8×1010K/s时，相变发生在1 810 K。

计算表明：①当冷却速度高于1.2×1011K/s时，固液相变发生的温度低于912℃（1 185 K），位于体心立方的α-Fe是稳定相；②当冷却速度高于6×1010K/s低于1.2×1011K/s时，固液相变温度位于面心立方γ-Fe的稳定区；③当冷却速度低于1.8×1010K/s时，固液相变温度接近1 538℃（1 801 K），将形成过冷液体或体心立方结构的δ-Fe。

得到的结晶温度与冷却速度的关系见图3。由以上结果可知，随着冷却速度的降低，发生相变的温度增大，过冷度降低。冷却速度低于1.8× 1010K/s时结晶相变点和熔点基本重合，理论计算快速冷却过程中，铁熔体的过冷度可达到800K。由于冷却速度大于1.8×1012K/s观察不到相变，因此能形成晶体的区域过冷度可达到700 K。

3.2 铁熔体冷却过程中的径向分布函数（RDF）

RDF表现了体系中原子分布和径向位置的关系，对于判断体系结构有着重要意义。在温度较低时，RDF的峰清晰尖锐，各个峰所对应的值，对应原子周围最近邻、次近邻配位的位置，体现了规律的周期性晶体结构；随着温度升高，晶体的周期性结构逐渐解体，RDF的峰变宽，一些峰消失；直至到达液相，RDF的值不表示配位情况，而是反映了此时体系原子相对于中心原子位置的概率。

体系以6.5×1011K/s的速度降温时，末态结构的RDF如图4所示，结晶后2近邻原子、3近邻原子和4近邻原子最可几分布点，分别在1.15、1.65和1.98倍的最近邻位置，这一结论和体心立方的格点排布相同。

图3 结晶温度与冷却速度的关系曲线Fig.3Curve of crystallization temperature and cooling rate

图4 冷却速度为6.5×1011K/s时，末态的RDFFig.4Curve of radial distribution function of iron in the final structure at cooling rate of 6.5×1011K/s

由Jackson界面平衡结构理论模型，晶体生长与相变时的温度（TCR）和前后的熵变（ΔS）有关。Jackson常数

当α＜2时无晶面生长，2＜α＜10时在生长过程中产生晶面。平衡情况下Fe液固相变α=1.02［6］，因而很难获得Fe单晶。考虑到快速冷却过程凝固温度TCR大幅度降低，同时相变过程中熵变ΔS也增大，快速冷却过程大幅度地提高了Jackson常数α。上述结果表明，在冷却速度为1011K/s附近可以生成体心立方Fe单晶。

4 结论

在分子动力学模拟铁熔体的快速冷却过程中，通过对8×8×8个原子的体系进行不同速度的降温，得到能量曲线和RDF，得出如下结论：

1）冷却速度低于1.8×1010K/s时，结晶相变点和熔点基本重合，铁熔体的过冷度可达到700 K。

2）铁熔体冷却速度为1012K/s以上时，生成物为非晶。

3）在冷却速度为1011K/s附近可以生成体心立方Fe单晶。

（References）

［1］ZHOU Y H，NIE C，TIAN H Y，et al.Investigation on the synthesis mechanism ofβ-FeSi2prepared by pulsed laser deposition［J］.Wuhan University Journal of Natural Sciences，2012，17（1）：61-66.

［2］陈景榕，李承基.金属与合金中的固态相变［M］.北京：冶金工业出版社，1997：13-16.

［3］邵琛玮，王振华，李艳男，等.AuCu249合金团簇热稳定性的原子尺度计算研究［J］.物理学报，2011，60（8）：083602-083610.

［4］王丽，边秀房，李辉.金属Cu熔化结晶过程的分子动力学模拟［J］.化学物理学报，2000，13（5）：544-550.

［5］陈光，傅恒志.非平衡凝固新型金属材料［M］.北京：科学出版社，2004：1-19.

［6］MOULSON A J，HERBERT J M.Electroceramics：ma⁃terials，properties，applications［M］.2nd ed.Hobo⁃ken，NJ：John Wiley&Sons，2003：122-125.

（责任编辑：曾婷）

Molecular Dynamics Simulation of Rapid Cooling Process of Iron Melt

ZHOU Youhua，LI Wenhui，TAO Lei，ZHENG Guang
（School of Physics and Information Engineering，Jianghan University，Wuhan 430056，Hubei，China）

Establishes 8×8×8 atomic box with LAMMPS，adopts EAM（embedded atom model）potential，to simulate large number iron atoms system.At first，heats up the system，then cool down the system under different cooling rate.Through molecular dynamics simulation，obtains energy-tem⁃perature curve，radial distribution function（RDF）and architecture.The results show that the crystal⁃lization temperature point is basically in coincident with the melting point when the cooling rate is lower than 1.8×1010K/s；the product is amorphous when the cooling rate is higher than 1012K/s；the degree of supercooling can reach 700 K；Fe single crystal can be prepared at cooling rate around 1011K/s.

molecular dynamics simulation；rapid cooling；iron melt

O561.1

A

1673-0143（2014）03-0037-04

2014-04-02

国家自然科学基金资助项目（61240056）

周幼华（1969—），男，副教授，博士，研究方向：功能薄膜、半导体薄膜、新型光电器件的开发。