组织工程多孔支架微管内流场数值模拟

蒋静智，贾超，郭彦书

（河北科技大学机械工程学院，河北 石家庄 050018）

组织工程支架是指能与组织活体细胞结合并能植入生物体的三维结构体，是组织工程化的最基本构架[1]。它要求除具有良好的生物相容性、适宜的降解性和有效的表面活性外，还要求具有合适体积、形状的三维外部立体结构，以及高孔隙率且内部连通的三维内部结构，以便为种子细胞增殖、长入支架材料以及养分交换和代谢产物的排出提供良好的空间和通道[2-3]。细胞培养过程中不管是种子细胞进入支架，还是其排泄废物排出支架，均需通过营养液将它们带入或带出。因此营养液和细胞或代谢废物在支架微管内的流动对于体外活体培养的成功起着至关重要的作用。但支架内部管网结构复杂，各管道的形状、管道大小及管道的粗糙程度都会对营养液在支架内的流动产生重要的影响。随着细胞的生长、增殖和支架材料的不断降解，支架的孔道形状及其结构不断发生变化，这使得支架内部各孔道里流体的流动变得愈加难以预测。

虽然目前国内外关于组织工程支架制备方面有大量文献报道，但支架体外培养作为组织工程临床应用的关键步骤，对于支架内营养液或细胞在微管内的流动特性研究仍处于起步阶段[4]，相关报道较少。徐尚龙等[5]利用CFX程序对细胞悬浮液在3种特定结构的骨工程支架内部的流动进行了模拟计算，给出了管道系统中细胞和细胞悬液两相流速度场、细胞浓度和压力的分布。赵静一等[6]对不同孔隙率和不同流量下的支架内流场进行了数值模拟，得到了支架内部的速度、压力分布图。王洋等[4]对于准静态平面流场的新型皮肤组织工程灌注式生物反应室进行了初步模拟。以上文献均取得了初步的研究结果，但一是其采用的模型支架结构较为简单，二是对于得到的数值模拟结果缺乏必要的流体力学理论分析。本文根据国内外人工骨的设计、发展状况，考虑实际人工骨的结构比例，建立三维人工骨支架模型，利用流体计算软件Fluent对细胞和营养液在骨支架内部各微管内的流动进行了数值模拟计算，给出了不同浮克曼管（图 1）长度、直径以及浮克曼管和主管道之间的夹角等几何结构参数对营养液和细胞在人工骨支架内部流动的流速和压力的影响，同时，基于生物流体力学、支架内部分叉流体力学的基本理论对模拟结果进行了系统理论分析，从而为支架结构的设计、改进及细胞培养过程中各参数的设定提供了有力的理论依据。

图1 人工骨支架微管结构示意图

1 物理模型

人工骨内部微细结构模型简化可知，骨质有密质骨和松质骨两种形态，松质骨结构简单，分布少。因而本文采用密质骨的微管结构来建立骨支架模型。骨组织支架中多个浮克曼管一端连接于哈佛氏管（图1），另一端与骨髓腔和骨外的循环系统连通，构成骨组织与外界交换和代谢的营养通道。密质骨的营养液循环是维持生命的活骨特性和骨折愈合的营养来源，而营养液的供应主要来源于哈佛氏管和浮克曼管，研究骨组织中浮克曼管和哈佛氏管内营养液和成骨细胞的流动对于细胞生长及骨组织成长起着至关重要的作用。

医学表明：一般浮克曼管与哈佛氏管的直径比为2∶3，主管道和浮克曼管夹角为0～180°，由于主管道和浮克曼管的夹角>90°时，会造成很大的阻力损失[7-8]，因此本文模拟人工骨主管道与浮克曼管的夹角分别为45°、75°和90°。由于营养液和骨细胞均需通过浮克曼管输送到骨支架中，骨支架微管内流动的流体为营养液和骨细胞组成的混合物。营养液密度为1100kg/m3，黏度为0.0018Pa·s，骨细胞密度为 1200kg/m3，骨细胞所占体积分数为0.02，混合液中比例很小，人体血液的平均流速为0.19m/s[9-10]，因而确定本文模拟的营养液和细胞的混合液密度近似为1100kg/m3，黏度为0.0018Pa·s，初始流速设为 0.19m/s。根据仿生骨的几何结构参数[11]，本文模拟的骨支架微管结构参数如表1所示。

表1 骨支架孔系结构设计参数

2 数学模型

虽然组织工程支架的孔道达到了微米级的尺度，在其流动特性上呈现出不同于宏观的流动规律。但是根据前人所做的大量微流体实验结果表明，宏观上仍满足流体质量守恒和动量守恒定律。因此本文的模型控制方程如下[12]。

质量守恒方程见式（1）。

黏性不可压缩流体动量守恒方程如式（2）～式（4）。

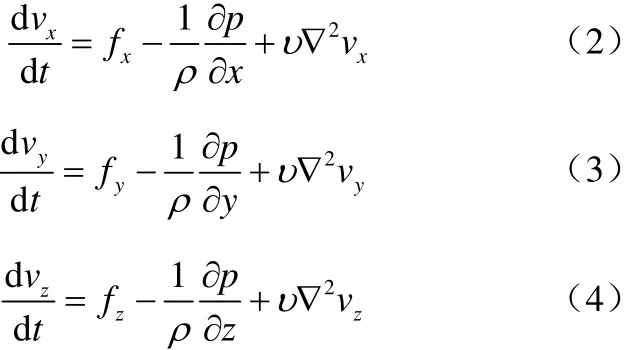
式中，qv0为进口流量；qv1为主管道出口流量；qvi为微管道出口流量；vx、vy、vz为流体在x、y、z方向的速度分量；fx、fx、fx为x、y、z方向上的单位质量力；p为表面上的压力；ρ为流体的密度；υ为流体的运动黏度。

3 Fluent参数设置

3.1 几何模型及网格划分

依据物理模型分析，采用 Fluent前处理软件Gambit建立组织工程支架几何模型并划分网格。选取骨架的中间主管道的上端面为进口，剩余所有圆柱的端面为出口。由于模型复杂、尺度小，采用了主管道为六面体，各微管连接处为四面体、锥形或楔形网格的形式划分网格，以此得到的网格质量好，计算精度高，计算时间短，且易收敛。经多次试算，确定网格数约为 13万个，最大网格体积约为2.975785×10−12m3，最小网格体积约为 1.655276×10−13m3。

3.2 计算参数设置

将Gambit输出的网格文件导入Fluent求解器中，由于本模拟的流体为不可压缩流体，采用压力基显式分离求解器进行求解。由于流体黏度高，流速低，求得主管道内流体的雷诺数Re为244左右，远远小于 2000，确定流体流动为不可压缩的层流流动。

4 模拟结果及分析

4.1 浮克曼管长度对骨支架微管流场的影响

图2(a)、2(b)、2(c)为X=0浮克曼管直径 0.6mm，与主管道夹角为90°，长度L分别为1.5mm、2mm和 3mm时营养液和细胞混合液在支架微管内流动的速度及压力分布图。由速度分布图可以看出，3种不同浮克曼管长度下的骨支架流场遵循同样的流动规律，从进口到出口，主管道内流体流速随管道的深入不断减小。上端浮克曼管中流体流速比下端浮克曼管中流体流速高，但是比同一高度主管道内流体流速低。哈佛氏管与第一行浮克曼管交叉处下端的哈佛氏管内流体的流动速度较为缓慢，随着浮克曼管长度的增长，该流动缓慢区域不断变小。但从第三行浮克曼管与哈佛氏管交叉处开始，其下端流体的速度不断增大。压力分布图与速度分布图呈现相似的规律性。

分析认为主管道中的流体流动到浮克曼管处分岔时，一是分流，二是会受到直角分岔管道的局部阻力，主管道内流体的流速沿流动方向不断减小。分岔管内的流体总是受到来流的速度和静压力的影响，来流速度越大，分叉管道内的速度越高[13]，因此，随主管内速度的减小，从上至下浮克曼管内流体的流速逐渐降低。主管道内的流体流入上端浮克曼管时，由于浮克曼管管径跟主管道管径相比较小，分流效应使得主管道内流体流入上端浮克曼管内的流速比同一高度主管道内流体流速低[13]。哈佛氏管内的流体既受到浮克曼管中流体的推动，也受到流动时沿程阻力的影响。来自于第一行浮克曼管中的流体距离上端出口较近，因此可以以较快的速度到达出口。由于第一行浮克曼管中流出的流体速度较大，第三行浮克曼管中流出的流体流速较小，通过第二行浮克曼管进入哈佛氏管的流体只能克服第三行浮克曼管中流出的流体的阻力而向下流动。流体黏性大，上下流动的阻力大，因此上端哈佛氏管内流体流动速度缓慢。当浮克曼管长度增大时，由于受到沿程阻力的作用，第一行浮克曼管中流体流出的速度逐渐减小，第二行浮克曼管中的流体能克服第一行浮克曼管中流出的流体阻力而向上流动，所以当浮克曼管的长度增加时，上端哈佛氏管中流体流动的缓慢区减小了。第三行浮克曼管及以下的浮克曼管的流体不断与哈佛氏管中的流体汇合，下端哈佛氏管内流体流速不断增加。当浮克曼管的长度到达 3mm时，各个浮克曼管中流体的流速更为均匀，有利于营养液和细胞的输送，所以浮克曼管长度选取3mm较为适宜。

图2 不同浮克曼管长度骨架内流体速度及压力分布图

4.2 浮克曼管管径大小对骨支架微管流场的影响

图2(c)、图3(a)、3 (b)为X=0浮克曼管长度3mm，与主管道夹角为90°，直径d分别为0.6mm、0.4mm和 0.8mm时营养液和细胞的混合液在支架微管中流动的速度和压力分布图。从速度分布图上看到，3种不同浮克曼管直径下的骨支架流场遵循的流动规律跟不同浮克曼管长度下的骨支架流场相似。图2(c)、图3(a)、图3(b)的速度分布图相比较，直径为0.4mm的骨支架浮克曼管内流体流动不顺畅，流速低，主管道内的流体流速虽然随着主管道的深入有所减小，但不明显；哈佛氏管内流体流动缓慢区增大。流体在浮克曼管直径 0.8mm的骨支架内流动时，主管道流速减小幅度较大，同时上端三层浮克曼管中流体流速大，但流体在下端浮克曼管中流速急剧降低，最下端浮克曼管中的流速几乎接近于零，这对于细胞和营养液的输运均带来不利的影响。压力分布图呈现流体流动的规律和速度分布图相同。

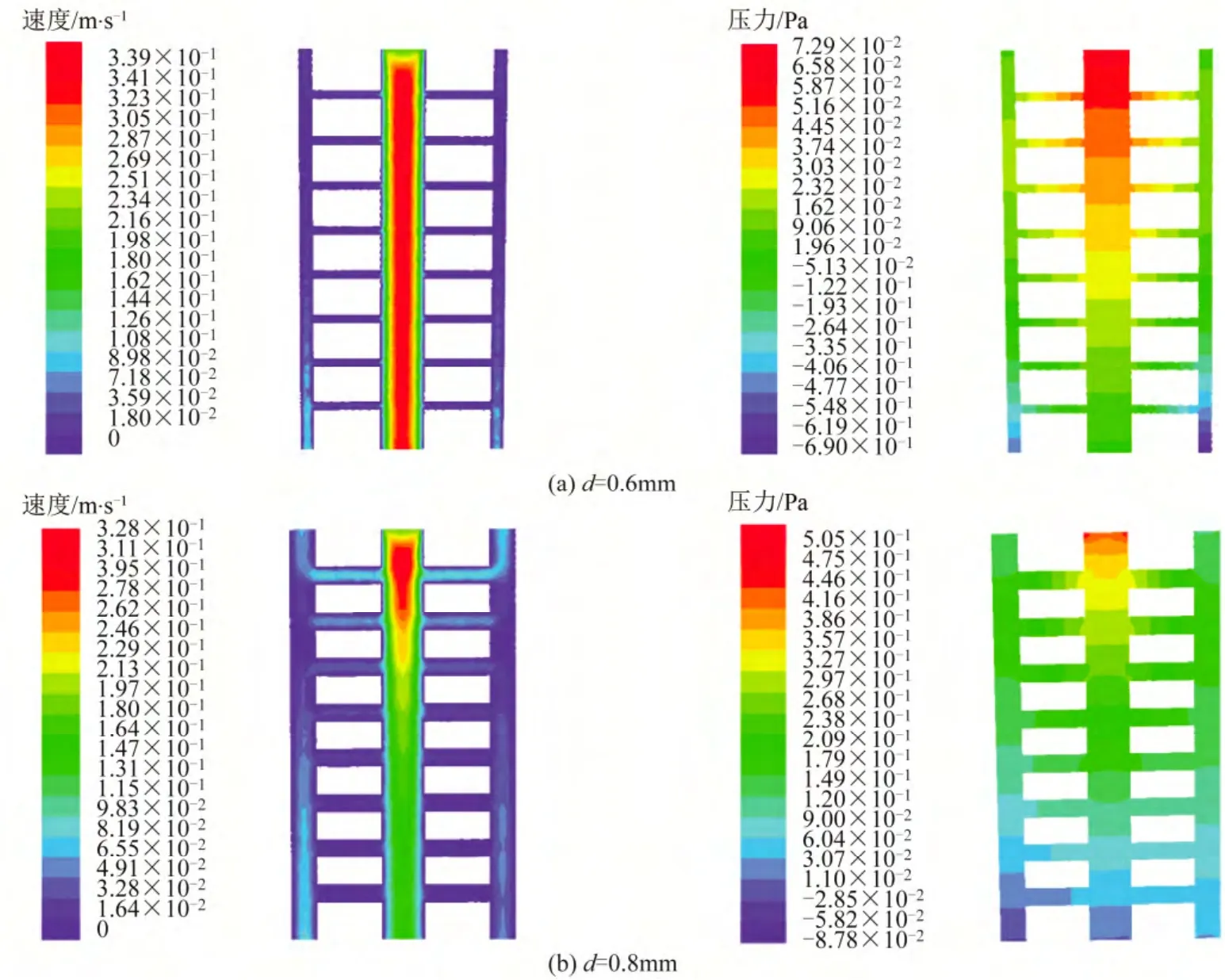
图3 不同浮克曼管直径骨架内流体速度及压力分布图

分析认为浮克曼管直径减小，入口处阻力增大，局部能量损失增大，主管道内的流体很难流入浮克曼管中，大部分流体将沿主管道从上向下流动。随着浮克曼管直径增大，入口阻力减小，各浮克曼中流体流量增加，因此，上端三层浮克曼管中流体有较大的流速，导致主管道内的流体流速自上向下降低很快。主管道内的流体再经过浮克曼管时，来流速度降低，加之于主管道与浮克曼管分岔处的局部阻力和浮克曼管中的沿程阻力，主管道内的流体流入下端浮克曼管很困难，所以下端浮克曼管中流速很低。综合图2(c)、3(a)、3(b)的速度分布图，浮克曼管长度 3mm，与主管道夹角为 90°，直径为0.6mm的骨支架下端浮克曼管内流体流速比较均匀，有利于细胞和营养液在浮克曼管和哈佛氏管中流动，有利于骨的生长，所以，浮克曼管直径选取0.6mm比较适宜。

4.3 浮克曼管与主管道夹角大小对骨支架微管流场的影响

图2(c)、图 4(a)、4(b)为X=0浮克曼管长度为3mm，直径为0.6mm，浮克曼管与主管道夹角θ分别为90°、45°和75°时营养液和细胞的混合液在人工骨支架模型中流动的速度和压力分布图，从图中可以看出，3种不同角度下主管道内的流体速度呈现相似性，其流速降低幅度相差不多。当夹角为45°时，上端浮克曼管中的流体流速较大，达到了6.28×10−2m/s，但是哈佛氏管中流动缓慢区增大，几乎占到哈佛氏管高度的一半。在此流动状况下，当细胞和营养液输运时，细胞易于在此处聚集和堵塞管道，从而可能会造成细胞的死亡。随着夹角的增大，上端两层浮克曼管中流体流速逐渐减小，流体在主管道与浮克曼管夹角分别为75°和90°时，上端浮克曼管中流体的速度分别为 5.05×10−2m/s和4.99×10−2m/s；同时，随着夹角的增大，哈佛氏管内流体流动缓慢区域逐渐减小。夹角为90°的支架各微管内流体流动速度更为均匀，因而更有利于细胞和营养液的输运。

图4 不同浮克曼管与主管道夹角角度时骨架内流体速度及压力分布图

分析认为浮克曼管与主管道的夹角越小，主管道与浮克曼管交叉处的局部阻力也就越小，流体易于流入浮克曼管中。但在骨支架模型上端，流体从上端出口流出，此时当流体从浮克曼管中流入哈佛氏管时，由于发生大于90°的绕角流，此处的流动阻力明显增加，流速迅速降低。此结果在该支架微管模型的中间部位影响非常明显，从图4可以看出，中间位置的浮克曼管和主管道的静压力基本相等，说明此时浮克曼管中的流速很低，因而夹角为45°和 75°的骨架内哈佛氏管中流动缓慢区相比 90°均有所增大。由于主管道上端大部分流体被浮克曼管分流，当流体流入主管道下部时，此时流量和流速均减小，虽然到达主管道下部时，流体从哈佛氏管下端口流出，此时夹角分别为45°、75°的支架微管内，不管是流体从主管道流入浮克曼管还是从浮克曼管流入哈佛氏管，流体的流动都较为顺畅，但其流动均匀区域在整个支架微管内仍占有较小的一部分，该种夹角的支架不适于骨组织工程的应用。从流体力学基本理论来说[14]，当流体流经夹角较小的两个管道时，易于形成流动的“死区”，在该区域流体流动停止。对于组织工程支架，出现如此的流动区域，极易造成细胞的死亡和管道的堵塞，因而组织工程人工支架以浮克曼管和主管道夹角为90°更为适宜。

5 结 论

利用流体计算软件Fluent对不同尺寸的人工骨支架微管内细胞和营养液的流动进行了数值模拟计算，当浮克曼管的管径和长度、与主管道夹角角度不同时，基于各微管的分流效应，主管道和各微管内的速度和压力分布各不相同。本文模拟范围内，浮克曼管长度3mm，直径0.6mm，浮克曼管与主管道夹角90°的人工骨支架内流体流速均匀，流动顺畅，流场环境不仅有利于细胞沉积和均匀黏附，而且利于骨支架内的血液循环和营养物质的代谢与交换，更加适合人工骨支架结构。利用Fluent对组织工程支架内部微管内流体流动的模拟计算和分析可为组织工程支架内部结构设计提供一定的数据和理论依据。

[1]Debanjan Sarker，Zhao Weian，Sebastian Schaefer，et al.Biomaterials Science[M].Royal Society of Chemistry，2013：1122-1137.

[2]刘淑琼，许祯毅，刘瑞来.纳米纤维应用与组织工程的研究进展[J].化工进展，2012，31（12）：2743-2747.

[3]Liu Yuchun，Jing Lim，Swee-Hin Teoh.Review：Development of clinically relevant scaffolds for vascularized bone tissue engineering[J].Biotechnology Advances，2013，5（31）：688-705.

[4]王洋，蔡伟华，伍津津，等.基于准静态平面流场的新型皮肤组织工程灌注式生物反应室设计与初步模拟[J].第三军医大学学报，2013，35（7）：622-626.

[5]徐尚龙，李涤尘，卢秉恒.人工骨体外微管道内细胞及细胞悬液两相流数值研究[J].机械工程学报，2006（3）：40-45.

[6]赵静一，李侃，吴厚正，等.组织工程支架内流场的数值模拟[J].液压与气动，2006（7）：19-21.

[7]Emerson dos Reis，Leonardo Goldstein Jr.Fluid dynamics of horizontal air-water slug flows through a dividing T-junction[J].International Journal of Multiphase，2013，50：58-70.

[8]陶祖莱.生物流体力学[M].北京：科学出版社，1984.

[9]秦任甲.血液流变学[M].北京：人民卫生出版社，1999.

[10]Philippe Connes，Stephane Dufour，Aurelien Pichon，et al.Nutrition and Enhanced Sports Performance[M].Amstardam：Elsevier，2013：283-293.

[11]朱晓龙，李占利.人工活性骨内部结构建模方法研究[J].西安科技学院学报，2003，23（2）：212-215..

[12]马哲一.骨组织工程支架内微流体流动状态的数值仿真及分析[D].秦皇岛：燕山大学，2009.

[13]Lu T，Attinger D，Liu S M.Large-eddy simulations of velocity and temperature fluctuations in hot and cold fluid mixing in a tree junction with an upstream straight or elbow main pipe[J].Nuclear Engineering and Design，2013，263：32-41.

[14]黄卫星，陈文梅.工程流体力学[M].北京：化学工业出版社，2001.