中天山乌拉斯台地区矿化异常提取及评价
辛存林,董 凯,孟 健,朱多录,马维云,巩 鑫,朱晓磊
(1. 西北师范大学地理与环境科学学院,甘肃兰州 730070;2. 防灾科技学院地震科学系,河北三河 065201;3. 云南省地质调查院,云南昆明 650051)
中天山乌拉斯台地区矿化异常提取及评价
辛存林1,董 凯1,孟 健2,朱多录3,马维云1,巩 鑫1,朱晓磊1
(1. 西北师范大学地理与环境科学学院,甘肃兰州 730070;2. 防灾科技学院地震科学系,河北三河 065201;3. 云南省地质调查院,云南昆明 650051)
以多重分形理论为基础,对中天山乌拉斯台地区铜多金属元素的岩屑测量数据,采用C-A法获得铜多金属的异常下限值,将其作为阈值进行指示克里格插值,绘制研究区的铜多金属地球化学异常图。研究显示,基于该方法获得的Cu矿化异常高值区主要集中在华力西早期第三侵入次的石英闪长岩和花岗闪长岩岩体中,受北西向和次级北东向断裂构造控制明显,该异常区可以作为寻找热液型铜多金属矿产的重要远景区。该方法对于地球化学数据空间变异性强烈的地区,较之普通克里格插值法具有更好的地球化学异常识别能力和高值信息重建能力,所得结果的最高累计频率值范围与已知矿化点的空间位置吻合度更高,在地球化学异常信息提取工作中具有推广意义。
指示克里格法 C-A法 变异函数 浓度-面积模型 地球化学异常
Xin Cun-lin, Dong Kai, Meng Jian, Zhu Duo-lu, Ma Wei-yun, Gong Xin, Zhu Xiao-lei. The extraction and assessment of anomalies of mineralization in Wulasita area of the middle Tianshan[J]. Geology and Exploration, 2014, 50(2):0382-0390.
在勘查地球化学领域,以地质统计学为基础的普通克里格插值法在地球化学异常提取中被广泛应用(孙洪泉,1990;成秋明,2001;张仁铎,2005)。普通克里格插值法是区域化变量的线性估计,假设数据变化呈正态分布,在有限区域内对区域化变量进行无偏最优估计的一种方法(李晓晖等,2011)。该方法基于滑动加权平均原理,以变异函数为基础对局部范围进行加权平均,因而不可避免地对数据造成平滑效应,从而无法完全实现原始地球化学高值异常信息的重建,这对于地球化学异常的识别是极其不利的(黄竞先等,1994;陈伯茂,2009)。而指示克里格方法不需要了解区域内每一个点的属性值,只需了解属性值是否超过某一阈值,对于具有异常值和偏态分布的数据都具有良好的稳健能力(纪宏金等,2001;李庆谋,2005)。通过设定表征异常下限的阈值可以获取小于或大于该阈值的累计频率,从空间频率域为地球化学数据的异常识别提供科学依据(成秋明,2009;李晓晖等,2011)。多重分形理论的提出为异常下限值的确定提供了有利的前提,由于地球化学场不仅具有结构性变化特征,还具有随机性变化特征(成秋明,2006)。这种随机性变化往往由矿化异常引起,具有尺度不变性特征并可由多重分形模型定量表征。基于非线性模型的多重分形技术,根据地球化学场的自相似性特征将其分解为不同的空间模式,从而实现地球化学场背景和异常的分离,克服了传统的统计方法不考虑样品空间分布和传统特征随空间度量尺度变化性的不足(成秋明,2000;谢淑云等,2002)。
本文以中天山乌拉斯台地区铜多金属元素岩屑地球化学数据为基础,利用多重分形(C-A)法确定该地区铜多金属异常下限,并以该异常下限值作为阈值,用指示克里格法进行插值,提取高于该阈值的概率分布信息,对该概率分布在空间结构变化特征及其控制因素进行研究,提取研究区内与矿化有关的异常信息。
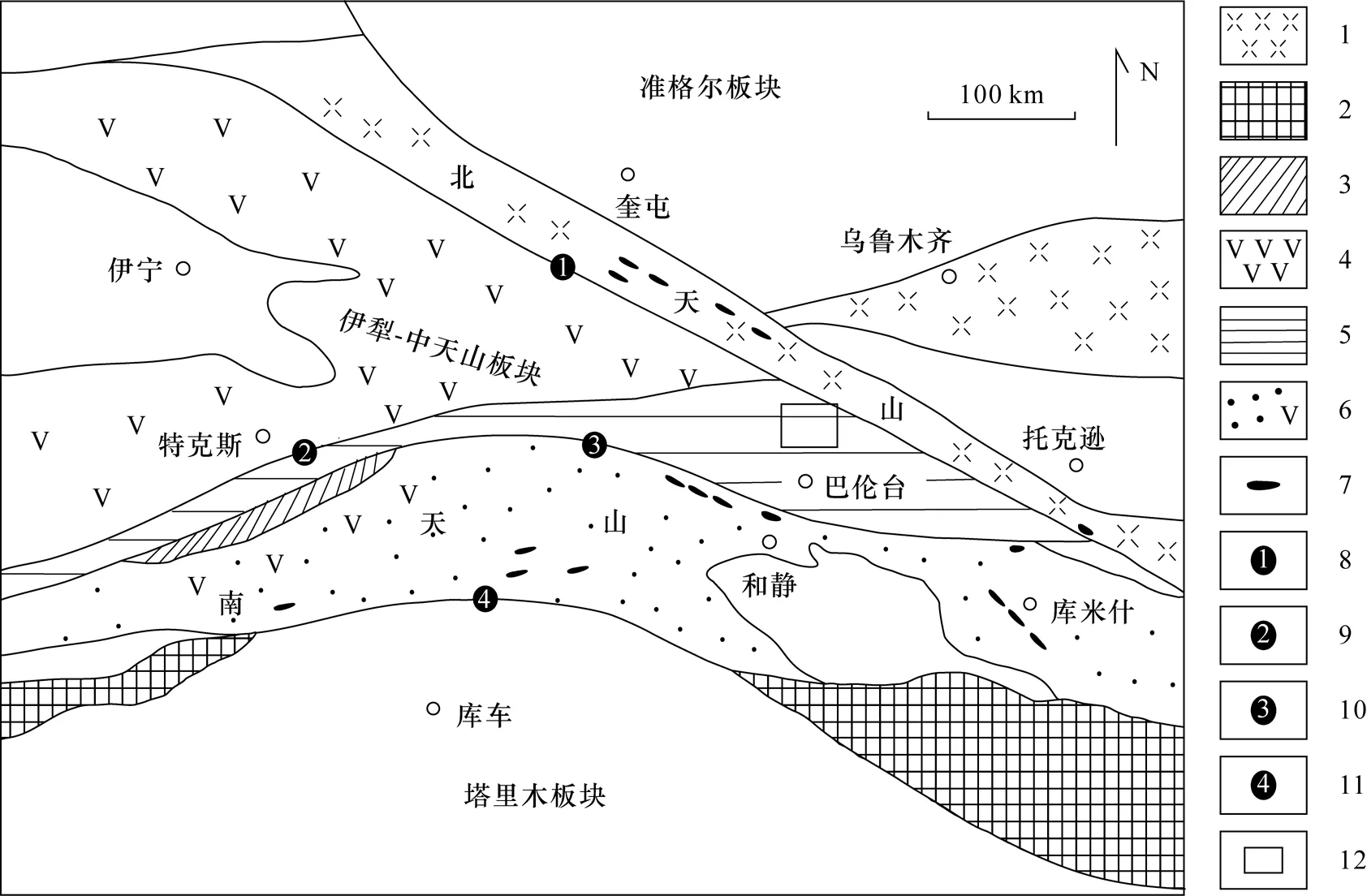
图1 中天山构造略图及地理位置 (据新疆地质局,1975和王洪亮等,2007修改)Fig.1 Structural map and geographical position of Middle Tianshan (modified from Xinjiang Geological Bureau, 1975 and Wang et al., 2007) 1-早古生代火山沉积岩系;2-前寒武纪变质岩系;3-低温-高压变质岩;4-前寒武纪变质地层叠加古生代火山沉积岩系;5-前寒武纪变质地层叠加古生代岩浆岩;6-寒武纪-奥陶纪沉积地层(“V”表示少量火山岩出露);7-志留纪-早石炭纪蛇绿混杂岩;8-中天山北 缘断裂带(NTS);9-那拉提北缘断裂带(NNF);10-中天山南缘断裂带(SCTS);11-塔里木北缘断裂带(NTF);12-研究区位置1-early Paleozoic volcano-sedimentary rock system; 2-Precambrian metamorphic rock series; 3-low temperature-high pressure metamorphic rocks; 4-superposition of Paleozoic volcanic sedimentary rock series in Precambrian metamorphic strata; 5-superposition of Paleozoic magmatic rock in Precambrian metamorphic strata; 6-Cambrian-Ordovician sedimentary formation; 7-Silurian-early Carboniferous ophiolitic mélange; 8-fault zone in northern margin of central Tianshan Mountains; 9-fault zone in northern margin of the Nalati; 10-fault zone in southern margin of central Tianshan Mountains; 11-fault zone in northern margin of the Tarim; 12-research area
1 成矿地质背景
天山是中国大陆西部重要的一条大陆造山带,经历了多期构造变形及岩浆活动(张立飞等,2005)。研究区位于中天山北缘断裂和中天山南缘断裂之间的伊犁-中天山板块,属于天山南脉地槽褶皱带上的巴伦台隆起,是萨阿尔明金铜多金属成矿带的一部分。区域地层属于准噶尔北天山地层分区上的伊林哈比尔尕地层小区。区域内断裂发育,主要构造线呈北西向展布(图1)。
研究区受构造活动的影响,中酸性侵入岩发育,主要为华力西早期第三侵入次闪长岩、花岗闪长岩、花岗岩,并具有同源多期侵入特点;区内主要出露地层有泥盆系上统天格尔组、志留系阿河布拉克组,在各地质单元中古生界志留系、石炭系地层富集元素众多,几乎包含了全部主成矿元素;铜元素在各地质单元中均表现出极不均匀分布状态,最具成矿潜力(图2)。
如表1所示,研究区中Cu,Ag,Pb,Bi的平均含量均远大于地壳克拉克值,均属于相对富集。变异系数相对较高,其活化和迁移作用也很强烈,其元素异常主要分布于华力西第三侵入次石英闪长岩和花岗闪长岩的岩体中,异常相对比较明显。在野外地质调查中,发现主要的铜矿化点就位于华力西早期第三侵入次花岗闪长岩的绿泥石化蚀变带中。受断裂破碎带的影响强烈,矿化部位岩石破碎程度愈高,矿化往往越明显。研究区华力西第三侵入次石英闪长岩和花岗闪长岩具备形成铜多金属矿产的地球化学条件。

图2 乌拉斯台地区地质略图(据焉耆幅1∶20万区域地质矿产图修编)Fig.2 Geological map of Wulasitai area (After the 1∶200000 Yanqi geological map of regional geology and mineral resources in Xinjiang) 1-天格尔组第二亚组凝灰岩;2-天格尔组第二亚组片麻岩;3-阿河布拉克组第三亚组砂岩;4-华力西早期第二侵入次辉石角闪岩;5-华力早期第三侵入次黑云母石英闪长岩;6-华力西早期第三侵入次石英闪长岩;7-华力西早期第三侵入次花岗闪长岩;8-华力西晚期第 三侵入次花岗岩;9-研究区位置;10-地质界线;11-断裂;12-推测断裂;13-铜矿化点1-tuff in second submember of Tengger Fm.; 2-geniss in second submember of Tengger Fm.; 3-sandstone in third submember of Ahebulak Fm.; 4-early Variscan pyroxeneamphibolite of second intrusion; 5-The third intrusion of biotite quartz diorite in early Variscan movement; 6-early Variscan quartz diorite of third intrusion; 7-early Variscan biotite granodiorite of third intrusion; 8-late Variscan biotite granite of third intrusion; 9 -research area; 10-geological boundary; 11-fault; 12-inferred fault; 13-copper mineralized spot

元素平均含量标准离差变异系数浓度克拉克值地壳克拉克值Au2.761.610.580.634.38Ag0.462.876.236.570.07Cu195.591806.999.234.1647Pb45.28618.0913.653.0215Zn44.5145.831.030.5483Mn527.72734.541.390.531000Mo0.520.450.870.471.1W0.890.510.570.01160Sb0.320.250.780.640.5Bi0.261.204.625.330.05
注:样品由核工业新疆理化分析测试中心分析,2011;Au元素的含量单位为10-9,其余元素的含量单位为10-6。
2 铜多金属地球化学异常下限的确定
2.1 基本原理
地球化学异常下限的确定是地球化学异常评价的重要工作之一。传统的地球化学异常下限的确定主要是使用经典的统计学方法,以样品数据呈正态分布为假设前提,通过计算数据的统计学参数对异常下限进行确定,一般是以平均值与n倍的标准离差之和作为地球化学异常下限值(文战久等,2007;熊超等,2013)。该方法仅适用于地球化学数据呈正态分布或对数正态分布的情况,最新的研究表明元素的地球化学分布并不局限于正态分布或对数正态分布(白晓宇等,2008)。非正态分布或对数非正态分布的元素数据具有不规则性和自相似性,具有典型的分形特征,因此可以作为分形来处理(Cheng, 1999)。分形分布的特点要求大于等于某一尺度的数目或数,与物体大小之间存在幂函数关系,即
N(r)=Cr-D,r>0
(1)
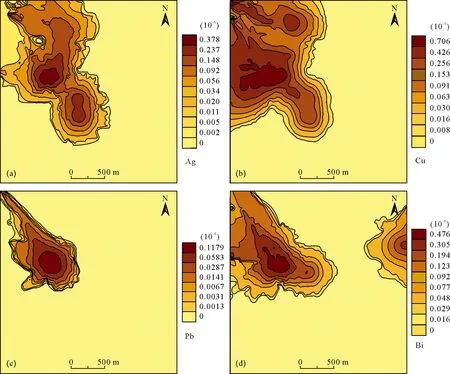
其中r表示特征尺度,C>0称为比例常数,D>0称为分维数,N(r)表示尺度大于等于r的数目。这里是对于所有满足xi≥r的i求和,Minxi≤r≤Maxxi。这样得到了数据集(N(ri),ri)(i=1, 2, 3, …,n lnN(r)=-Dlnr+lnC (2) 用最小二乘法求出斜率D的估计量,即分维数;如果其散点大致分布在两段直线上时,可以采用分段拟合,有的分界点清楚,有的则不清楚,为了提高分界点确定的客观性,在两个区间用最小二乘法进行回归时用最优化方法确定分界点(成秋明,2007;Chengetal. 1994)。其基本思想是,找出合适的分界点r0,使各区间拟合的直线与原始数据之间的剩余平方和Ei(i=1, 2)在两个区间的总和E最小。 (3) 其中ri0是分界点;D1和D2分别为相应区间的斜率即分维数。为了检验回归方程的显著性,对每个回归方程进行相关系数及方差分析检验。分界点的地质意义可以看成元素含量在空间上至少存在两个层次的分布,即小于分界点ri0对应的值为元素含量的背景分布,大于分界点ri0对应的值为元素含量的异常分布,ri0对应的值为元素含量分布的异常下限(Alietal. 2007;孙凯等,2011)。 2.2 异常下限的确定 用分形方法确定化探异常比传统的异常计算方法的优势在于不受元素特高值的影响,含量-面积分形方法将特高值形成的面积限定在一个很小范围内(仅影响特高值周围),不对整体数据产生影响(Chenetal. 2007;许顺山等,1999)。因此,用含量-面积的分形方法确定异常下限时不用对原始数据进行处理,减少了人为因素的干扰。 采用含量-面积法确定中天山乌拉斯台地区1∶1万岩屑样测量数据Cu,Ag,Pb,Bi 4种元素的异常下限,使用反距离加权法将地球化学元素数据网格化,绘制元素含量等值线图,统计N(r)为以等值线为r值所围成的平面面积,显然N(r)是递减函数。得到数据(N(r1) ,N(r2) , …,N(rn))和(r1,r2, …,rn)。应用这些统计数据在lgr-lgN(r)坐标中投点,用最小二乘法拟合二段直线,得到相应的直线方程及两条直线的交点ri0则为元素的异常值下限。由C-A法获取的双对数图(图3)和所对应的直线的参数(表2)可知,确定的Ag,Cu,Pb和Bi异常下限值分别为:0.5×10-6、240×10-6、120×10-6和0.5×10-6,其中拟合系数r2均接近于1,该值可以作为圈定铜多金属异常的异常下限。 表2 拟合直线方程参数及异常下限值Table 2 Equation of fitted line and the threshold 3.1 指示克里格法的基本原理 指示克里格法属于非线性克里格方法范畴,可用于估计某一位置超过指定阈值zk的累计频率(张仁铎,2005;李晓晖等,2011)。与普通克里格法相比,它不严格依赖于空间现象的平稳性假设,也不要求区域化变量服从某种分布;并且由于其在插值前根据一定的阈值将数据转换为指示变量,所以对于异常值和偏态分布都具有良好的稳健功能(阴江宁等, 2012)。指示变量的变换公式为: (4) 式中zk为设定的阈值。如果样品数据大于等于zk,则赋予指示变量0;如果小于zk,则赋予指示变量1。与普通克里格方法相似,对于任何一个待估点x0,z(x)≤zk的概率可以通过对相邻域内指示变量进行线性相加获得。普通指示克里格估值公式为: (5) 式中:i(xα;zk)表示xα(α=1,…,n)位置处的指示变量,λα是i(xα;zk)的克里格权重,可以通过求解克里格方程组得到。普通指示克里格方程组为: (6) 图3 C-A多重分形模型双对数图Fig.3 ln-ln plots of C-A multifractal model a-Ag多重分形模型双对数图;b-Cu多重分形模型双对数图;c-Pb多重分形模型双对数图;d-Bi多重分形模型双对数图a-lgN(r)-lgr plot of Ag showing relationship between “areas” and power-spectra; b-lgN(r)-lgr plot of Cu showing relationship between “areas” and power-spectra; c-lgN(r)-lgr plot of Pb showing relationship between “areas” and power-spectra; d-lgN(r)-lgr plot of Bi showing relationship between “areas” and power-spectra 式中:μ是拉格朗日算子,γi(xα-xβ;zk)是第α个和第β个样品点的指示变量的变异函数值(成秋明等,2009);γi(xα-xo;zk)是待估点x0与第α个样品点的指示变量的变异函数值。指示克里格方法采用的实验变异函数计算方法同普通克里格方法基本相同,不同的是指示克里格方法采用指示变量计算实验变异函数,公式为: (7) 式中:N代表滞后距离区间h内的样品对数。上述公式计算得到的实验变异函数值γ(h)还需通过拟合求解理论变异函数的参数,从而参与指示克里格方程组的计算(黄静宁等,2011)。 3.2 空间变异分析 变异函数分析是了解数据空间变异性质的有效工具,也是克里格插值的必要条件(阴江宁等,2012;张磊等,2009)。指示克里格方法下的变异函数采用C-A方法获取的异常下限值作为阈值参数。由于本文侧重高值异常信息,因此对于大于所定义阈值的样品数据赋予指示变量1,如果小于定义阈值则赋予指示变量0。通过Arcgis10软件计算了在指示克里格方法下的实验变异函数,从表3可见,研究区的元素含量变化呈现明显的各向异性,其基台值均为块金值的2倍以上,元素含量在变程范围内具有较强的相关性。在变差函数中表现为影响Cu,Ag,Bi和Pb元素连续性变化的最大变程分别为2.77km、2.17km、2.32km和2.45km,均在研究区中酸性岩浆岩对各元素的影响范围以内,具有较好的连续性。基于指示变量的实验变异函数则显示出良好的空间变异结构,变化趋势稳定且符合球状理论变异函数结构,很好地描述了空间数据的相关性和结构性。 表3 指示克里格法变异函数参数Table 3 Parameter of the variograms by indicator Kriging 3.3 铜多金属地球化学异常特征 由于研究区内存在大量高值异常数据,本文采用的基于C-A方法确定异常下限可以更为有效地求取指示克里格法的阈值参数,并参与指示克里格插值计算,可以更好地服务于针对具有多重分形性质的非平稳数据的异常识别研究。因此,可利用基于多重分形理论的指示克里格法和普通克里格法提取研究区的地球化学异常,并结合研究区地质特征对该区的地球化学异常特征及控矿因素进行讨论(图4、图5)。 指示克里格法获得的Cu异常主要集中在研究区西北部,分布面积较大,呈北西向展布。结合研究区地质特征,其高值区中心主要集中在华力西早期第三侵入次石英闪长岩和花岗闪长岩岩体中,异常的分布主要受研究区北西向和次级北东向断裂构造控制明显,在该异常带内沿北西向断裂有石英闪长岩和花岗闪长岩大量入侵和出露,表明该区曾有强烈的与Cu富集有关的多期次构造岩浆活动。研究区几乎所有铜矿化就位于该岩体中的断裂蚀变带上及附近。因此,该异常区可以作为寻找热液型铜矿产的重要远景区。 图4 普通克里格插值结果等值线图Fig.4 Contour maps of interpolation results by Kriging a-Ag的普通克里格插值结果等值线图;b-Cu的普通克里格插值结果等值线图;c-Pb的普通克里格插值结果等值线图;d-Bi的普通克里格插值结果等值线图a-The contour map of Ag with ordinary kriging; b-The contour map of Cu with ordinary kriging; c-The contour map of Pb with ordinary kriging; d-The contour map of Bi with ordinary kriging 图5 指示克里格插值结果等值线图Fig.5 Contour maps of interpolation results by indicator Kriging a-Ag的指示克里格插值结果等值线图;b-Cu的指示克里格插值结果等值线图;c-Pb的指示克里格插值结果等值线图;d-Bi的指示克里格插值结果等值线图a-The contour map of Ag with Indicator kriging method; b-The contour map of Cu with Indicator kriging method; c-The contour map of Pb with Indicator kriging method; d-The contour map of Bi with Indicator kriging method 指示克里格法获得的Ag,Bi,Pb异常主要集中在研究区西北部,也呈北西向展布。元素Ag,Bi,Pb均属于中低温元素,易在酸性岩体中富集。结合研究区地质背景来看,其异常均受北西向次断裂构造和北东向断裂构造的控制较为明显,反映了研究区内岩浆热液活动时期中低温元素的富集阶段。Ag,Bi,Pb元素的高值区仅赋存在华力西早期第三侵入次花岗闪长岩的岩体中,处于北西向次断裂带和北东向断裂带的交汇处,与华力西早期第三侵入次花岗闪长岩中Cu元素的高值区较为重合,但面积相对较小。 因此,可推断Cu,Ag,Bi,Pb元素的富集不仅与华力西早期的中酸性岩浆入侵时岩浆气化的中低温热液活动有密切的关系,而且受断裂构造作用的影响强烈。该异常高值区可以为确定铜多金属找矿靶区提供依据。较之普通克里格插值法,基于C-A方法获取阈值的指示克里格方法则具有很好的地球化学异常识别能力和高值信息重建能力,能够更好的与已知矿化的空间位置吻合,突出反映原始数据的高值异常信息。 研究表明,基于多重分形C-A模型和指示克里格法对研究区的铜多金属矿化异常进行提取,提取的Cu矿化异常高值区主要集中在华力西早期第三侵入次石英闪长岩和花岗闪长岩岩体中,受北西向和次级北东向断裂构造控制明显,并且研究区几乎所有铜矿化就位于该岩体中的断裂蚀变带上及附近。该异常高值区可以作为寻找热液型铜多金属矿产的重要远景区。 由于地球化学元素的空间分布在特定空间域具有局部不均一性和各向异性,通常表现出服从多重分形分布的特征,由多重分形C-A模型提取的该地区铜多金属的异常下限相对于传统方法其结果更加客观;以该异常下限作为阈值参与指示克里格插值,较之于普通克里格法具有更好的地球化学异常识别能力和高值信息重建能力,所得结果的最高累计频率值范围与已知矿化点具有更好的空间吻合度,可以更为有效地进行地球化学异常识别研究。 Ali K, Cheng Q, Chen Z. 2007. Multifractal power spectrum and singularity analysis for modeling stream sediment geochemical distribution patterns to identify anomalies related to gold mineralization in Yunnan province, in south China[J]. Journal of Geochemistry: Exploration, Environment and Analysis, 7(4): 293-301 Bai Xiao-yu, Yuan Feng, Zhou Tao-fa, Li Xiang-ling, Zhang Xin, Fan Yu, Chen Xing-ren, Chen Yong-ning, Chen Fu-rong. 2008. The determination of geochemical abnormity of soil Cd in Tongling mining area using multifractal method[J]. Bulletin of Mineralogy, Petrology and Geochemistry, 27(3): 306-310(in Chinese with English abstract) Chen Bai-mao. 2009. Contribution of geostatistics to geo-exploration[J]. Geology and Prospecting, 45(6): 14-20(in Chinnese with English abstract) Cheng Q, Agterberg F, Ballantyne A. 1994. The separation of geochemical anomalies from background by fractal methods[J]. Geochemical Exploration, 51(2): 109-130 Cheng Q. 1999. Spatial and scaling modelling for geochemical nomaly separation[J]. Geochemical Exploration, 65(3): 175-194 Cheng Qiu-ming. 2000. Multifractal theory and geochemical element distribution pattern[J]. Science-Journal of China University of Geosciences, 25(3): 311-317(in Chinese with English abstract) Cheng Qiu-ming. 2001. Multiracial and geostatistic for characterizing local structure and singularity properties of exploration geochemical anomalies[J]. Earth Science-Journal of China University of Geosciences, 26(2): 161-166(in Chinese with English abstract) Cheng Qiu-ming. 2006. Singularity-generalized self-dimilarity-fractal spectrum(3S) models[J]. Earth science-journal of China University of Geosciences, 25(3): 337-348(in Chinese with English abstract) Cheng Qiu-ming. 2007. Singular mineralization processes and mineral resources quantitative prediction: new theories and methods[J]. Earth Science Frontiers, 14(5): 42-52 (in Chinese with English abstract) Cheng Qiu-ming, Zhao Peng-da, Chen Jian-guo, Xia Qing-lin, Chen Zhi-jun, Zhang Sheng-yuan, Xu De-yi, Xie Shu-yun, Wang Wen-lei. 2009. Application of singularity theory in prediction of tin and copper mineral deposits in Gejiu district, Yunnan, China: Weak information extraction and mixing information decomposition[J]. Earth Science-Journal of China University of Geosciences, 34(2): 232-242(in Chinese with English abstract) Chen Z, Cheng Q, Chen J. 2007. A novel iterative approach for mapping local singularities from geochemical data[J]. Nonlinear Processes in Geophysics, 14(3): 317-324 Huang Jing-ning, Zhao Peng-da. 2011. Extraction and assessment of Cu-Au anomalies of the east Tangshan ore-forming belt, northwestern China[J]. Earth Science-Journal of China University of Geosciences, 36(2): 317-325(in Chinese with English abstract) Huang Jin-xian, Hou Jin-ru. 1994. Application of universal Kriging and indicator Kriging for geochemical prospecting[J]. Earth Science-Journal of China University of Geosciences, 19(3): 321-328(in Chinese with English abstract) Ji Hong-jin, Lin Rui-qing, Zhou Yong-chang. 2001. A discussion about some data processing methods in geochemical exploration[J]. Geology and Prospecting, 37(4): 56-59(in Chinese with English abstract) Li Xiao-hui, Yuan Feng, Jia Cai, Zhang Ming-ming, Zhou Tao-fa. 2001. Study on anomaly recognition from geochemical data based on multifractal model and indicator kriging method[J]. Geography and Geo-Information Science, 27(6):23-31(in Chinese with English abstract) Li Qing-mou. 2005. Multifractal-krige interpolation method[J]. Advance in Earth Sciences, 20(2): 248-255(in Chinese with English abstract) Sun Hong-quan. 1990.Geostatistics and its application[M]. Xuzhou: China University of Mining and Technology Press: 1-252 (in Chinese) Sun Kai, Zhou Su, Miao Zhen-ping, Hu Bing, Huang Kai, Zhang Lin-lin, Qiu Rui-zhao, Hu Shao-hua. 2011. Secondary halo anomalies of the Yu’erya gold deposit in the Xiancaogou area, Hebei province and its prospecting prognosis[J]. Geology and Exploration, 47(4): 565-576 (in Chinese with English abstract) Wang Hong-liang, Xu Xue-yi, He Shi-ping, Chen Jun-lu. 2007. China Tianshan and its adjacent area geological map (1:100 million)[M]. Beijing: Geological Publishing House: 32-38(in Chinese with English abstract) Wen Zhan-jiu, Gao Xing, Yao Zhen-xing. 2007. Multifractal mode study of geochemical fields based on "element area-concentration" method [J]. Advances in Earth Science, 22(6): 598-604(in Chinese with English abstract) Xiong Chao, Ge Liang-quan, Wang Zhuo, Gu Yi, Luo Yao-yao, Liu Duan. 2013. Extraction of geochemical anomaly information based on fractal filtering with fast fourier transform[J]. Geology and Exploration, 49(1): 162-166(in Chinese with English abstract) Xinjiang Geology Bureau. 1975. The 1∶200000 survey instruction of regional geology and mineral resources in Yanqi[R]. 1-82 与常规情况相比,在岩溶地区进行桩基施工的不同点主要在于桩基施工过程中可能碰到岩溶裂隙、溶槽、溶沟、溶洞等,造成下列问题:钻孔内泥浆容易流失,软弱覆盖层孔壁易因缺乏泥浆水头维持而坍塌;钻锤突破溶洞顶板时容易因梅花孔而卡锤;因溶洞底部岩层大多与水平面存在斜角,在冲孔过程中钻锤容易偏斜;在混凝土浇筑过程中,混凝土可能冲破溶腔内土壁向溶洞内流失,造成混凝土方量损失,处理不当或将形成断桩。为避免上述问题,关键在于对溶洞形成有效封闭,保证桩基在钻孔及浇筑混凝土过程中不发生漏浆及坍塌。 Xu Shun-shan, Wu Gan-guo, Jiang Wan, Zhang Da, Chen Bei-lin, Xie Yan-xia. 1999. Studing on fractals of Zijinshan copper-gold deposit[J]. Geology and Exploration, 35(5): 50-52 (in Chinese with English abstract) Xie Shu-yun, Bao Zheng-yu. 2002. Continuous multifractal model of geochemical fields[J]. Geochemical, 31(2): 191-200(in Chinese with English abstract) Yin Jiang-ning, Xiao Ke-yan, Zou Wei, Wang Zhong, Lu Lu. 2012. Appiying geostatistics to extract geochemical information in east Tianshan[J]. Journal of Jilin University(Earth Science Edition), 42(3): 887-894(in Chinese with English abstract) Zhang Lei, Shen Wei. 2009. Application of fractal method in lower threshold definition of geochemistry anomaly in New South Wales area, Australia[J]. Geological Bulletin of China, 28(2): 246-249(in Chinese with English abstract) Zhang Li-fei, Ai Yong-liang, Li Qiang, Li Xu-ping, Song Shu-guang, Wei Chun-jing. 2005 The formation and tectonic evolution of UHP metamorphic belt in southwestern Tianshan[J], Xinjiang. Acta Petrologica Sinica, 21(4): 1029-1038(in Chinese with English abstract) Zhang Ren-duo. Theory and application of spatial variation [M]. Beijing: Science Press: 100-184 (in Chinese) [附中文参考文献] 白晓宇,袁 峰,周涛发,李湘凌,张 鑫,范 裕,陈兴仁,陈永宁,陈富荣.2008.多重分形方法识别铜陵矿区土壤中Cd的地球化学异常[J].矿物岩石地球化学通报,27(3):306-310 陈伯茂.2009.地质统计学对找矿勘探的贡献[J].地质与勘探, 45(6):14-20 成秋明.2000.多维分形理论和地球化学元素分布规律[J].地球科学-中国地质大学学报, 25(3):311-317 成秋明.2001. 多重分形与地质统计学方法用于勘查地球化学异常空间结构和奇异性分析[J].地球科学-中国地质大学学报,26(2):161-164 成秋明.2006.非线性成矿预测理论:多重分形奇异性-广义自相似性-分形谱系模型与方法[J].(地球科学)中国地质大学学报, 31(3):337-348 成秋明.2007.成矿过程奇异性与矿产预测定量化的新理论与新方法[J].地学前缘,14(5):42-53 成秋明,赵鹏大,陈建国,夏庆霖,陈志军, 张生元,徐德义,谢淑云,王文磊.2009.奇异性理论在个旧锡铜矿产资源预测中的应用:成矿弱信息提取和复合信息分解[J].地球科学-中国地质大学学报,34(2):232-242 黄静宁,赵鹏大.2011.东天山地区Cu-Au异常信息提取与评价[J].地球科学-中国地质大学学报, 36(2):317-325 黄竞先,侯景儒.1994.泛克立格法和指示克立格法在地球化学探矿中的应用[J].地球科学-中国地质大学学报,19(3):321-328 纪宏金,林瑞庆,周永昶.2001.关于若干化探数据处理方法的讨论[J].地质与勘探,37(4):56-59. 李晓晖,袁 峰,贾 蔡,张明明,周涛发.2011.基于多维分形模型与指示克里格方法的地球化学异常识别研究[J].地理与地理信息科学,27(6):23-31 李庆谋.2005.多维分形克里格方法[J].地球科学进展,20(2):248-255 王洪亮,徐学义,何世平,陈隽璐.2007.中国天山及邻区地质图(1∶100万)[M].北京: 地质出版社:32-38 文战久,高 星,姚振兴.2007.基于“元素含量-面积”模型方法的地球化学场的多重分形模式分析[J].地球科学进展,22(6):598-604 孙洪泉.1990.地质统计学及其应用[M]. 徐州:中国矿业大学出版杜:1-252 孙 凯,周 肃,缪振平,胡 兵,黄 凯,张琳琳,邱瑞照,胡少华. 2011. 河北峪耳崖金矿苋草沟区次生晕异常及找矿预测[J]. 地质与勘探,47(4):565-576 熊 超,葛良全,王 卓,谷 懿,罗耀耀,刘 端. 2013. 基于 FFT 分形滤波的地球化学异常信息提取[J]. 地质与勘探,49(1):162-166 新疆地质局. 1975. 焉耆幅1∶20万区域地质矿产调查说明书[R] . 1-82 许顺山,吴淦国,江 万,张 达,陈柏林,谢艳霞. 1999. 分形在紫金山矿床中的应用[J]. 地质与勘探,35(5):50-52 谢淑云,鲍征宇.2002.地球化学场的连续多重分形模式[J].地球化学,31(2):191-200 阴江宁,肖克炎,邹 伟,王 中,路 璐.2012.地质统计学在东天山化探信息提取中的应用[J].吉林大学学报(地球科学版), 887-894 张 磊,申 维.2009.分形方法在澳大利亚新南威尔士地区地球化学异常下限确定中的应用[J].地质通报, 28(2):246-249 张立飞,艾永亮,李 强,李旭平,宋述光,魏春景.2005.新疆西南天山超高压变质带的形成和演化[J].岩石学报, 21(4):1029-1038 张仁铎.2005.空间变异理论及应用[M].北京:科学出版社:100-184 The Extraction and Assessment of Anomalies of Mineralization in Wulasita Area of the Middle Tianshan XIN Cun-lin1, DONG Kai1, MENG Jian2, ZHU duo-lu3,MA Wei-yun1, GONG Xin1, ZHU Xiao-lei1 (1. College of Geography and Environmental Science, Northwest Normal University, Lanzhou,Gansu 730070; 2. Department of Earthquake Science, Institute of Disaster Prevention, Sanhe, Hebei 065201;3. Geological Survey of Yunnan Province, Kunming, Yunnan 650051) This paper calculates the threshold of geochemical data by using the concentration-area (C-A) medel, which is built on the talus sample survey data of Cu-poly metallic elements in Wulasitai field of Middle Tianshan, and then uses the threshold for the indicator kriging interpolation method. The results show that high anomaly area mainly related with the granodiorite and quartz diorite of early Variscan being the most favorable metallogenic prospect area. This subdivision can also be used as an focus of future studies. Meanwhile, compared with inverse ordinary Kriging method, the highest rank of cumulative probability which obtained by indicator kriging mrthod can effectively highlight the geochemical anomalies which associated with the known mineralization. Furthermore, for the strongly spatially variable data, indicator kriging method has more advantages in reconstruction of highly information and maintaining the robustess of variogram. indicator kriging, multifractal, geochemistry, concentration-area model 2013-04-23; 2013-8-23;[责任编辑]郝情情。 国家自然科学基金(编号:41262001)、甘肃省科技支撑基金(编号:1104FKCA116)、甘肃省自然科学基金(编号:1010RJZA020)联合资助。 辛存林(1967年-),男,2009年毕业于兰州大学,获博士学位,教授,硕士研究生导师,主要研究方向为地质矿产与勘查。E-mail:xincunling@163.com。 P618.51 A 0495-5331(2014)02-0382-9


3 基于指示克里格法铜多金属元素异常的分析




4 结论

