资源量分类中勘查工程间距的确定方法研究

高航校，任小华，郭 健

(1. 西北有色地质勘查局，陕西西安 710068；2. 中国冶金地质总局矿产资源研究院，北京 100025)

资源量分类中勘查工程间距的确定方法研究

高航校1，任小华1，郭 健2

(1. 西北有色地质勘查局，陕西西安 710068；2. 中国冶金地质总局矿产资源研究院，北京 100025)

国内外的地质勘查规范中，对矿产资源量的分类(地质可靠程度)均有标准的定义，但没有确定资源量分类工程间距的定量方法，导致矿产勘查工作经常出现质量隐患。本文用变异函数模型统计学方法探讨这一问题。变异函数的变程反映了空间上区域化变量之间相关性的大小，当矿体样品品位服从正态分布时，正态分布函数位置参数μ等于样品平均品位，形状参数σ等于样品品位标准差，样品品位的方差等于变异函数的基台值；在拐点之间即区间(μ-σ,μ+σ]，样品分布概率为0.6826，变异函数变程的0.6826倍(0.6826a)可作为划分控制资源量的分类工程间距；影响资源量分类可靠程度的主要因素是建立的理论变异函数模型的稳健性。

资源量分类 勘查工程间距 变程 变异函数 正态分布

Gao Hang-xiao，Ren Xiao-hua，Guo Jian. A method of determining grid spacing in surveys for classification of mineral reserves[J]. Geology and Exploration, 2014,50(2):0340-0345.

0 引言

目前，国内外对矿产资源量分类(地质可靠程度分类)中勘查工程间距的确定没有定量的标准。在国内地质资源量估算分类中，勘查工程间距确定方法较为简单。首先根据矿体的品位变化系数、厚度变化系数、矿体规模、矿体形态和构造条件等指标确定矿体的勘查类型，然后参照相应地质勘查规范所提供的参考勘查间距确定资源量分类的工程间距，存在问题主要在于影响确定勘查类型的指标受人为因素影响很大；在国外矿业发达国家则采用地质统计学方法，利用高速计算机和先进的矿业软件进行资源量估算和分类，效率高，可靠性增强，是未来矿产资源勘查评价的发展方向。但资源量分类的工程勘查间距确定仍不统一，一定程度上依赖资质人的认识。经过多年的矿产资源勘查实践，以及对国内外资源量分类中勘查工程间距确定方法的研究，提出利用矿体内样品品位正态分布函数的特征点分布概率，确定变异函数的变程，进行资源量的定量分类方法，从而使资源量分类的勘查工程间距确定标准统一化、定量化、科学化。

1 固体矿产资源分类标准

中华人民共和国《固体矿产资源/储量分类》(GB/T17766—1999)约定矿产资源是指查明矿产资源的一部分和潜在矿产资源。GB/T17766—1999将经过勘查而未进行可行性研究或预可行性研究的内蕴经济的矿产资源根据地质可靠程度分为三类：

(1) 探明的内蕴经济资源量(331)；

(2) 控制的内蕴经济资源量(332)；

(3) 推断的内蕴经济资源量(333)。

在澳大利亚JORC标准体系中也有类似的分类。

本文主要研究使用变异函数的变程对经过勘查而未进行可行性研究或预可行性研究的内蕴经济矿产资源的类别进行分类的理论依据及方法。

2 利用变异函数变程进行资源量分类的依据

变异函数是地质统计学所特有的基本工具，通过随机性反映区域化变量的结构性。严格的变程是变异函数上升到95%基台值时的区域化变量的间距。区域化变量的变程反映了区域化变量的影响范围，即空间上两个变量之间相关的最大距离。当两个变量间距离小于变程时，其空间上是相依的，变程越小相关性越强；大于变程时，其空间上是无关的。

进行资源量分类的目的是划定矿产资源在空间上分布的可靠程度。因此，可以通过变异函数的变程进行资源量分类。

3 变异函数计算的前提条件

变异函数的计算理论上需要满足一些基本假设条件：

(1) 平稳性假设

在数据平稳的假设条件下，具有相同分割距离矢量的数据对有相同的空间相似性。从而满足了在空间环境中的统计重复性，是对随机变量的一个比较严格的假设条件。

(2) 二阶平稳性假设

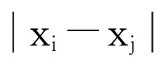
(3) 内蕴假设

内蕴假设要求Z(x)的增量Z(x+h)-Z(x)的数学期望和协方差存在，且与点x无关(即增量的平均值和方差为常量)。

(4) 准平稳假设

准平稳假设假定Z(x)只在有限大小的范围内是平稳的或内蕴的。

平稳性和二阶平稳性都是区域化变量的区域化平稳，在实际勘查工作中往往很难得到满足。而内蕴假设和准平稳假设只要求区域化变量的增量满足平稳条件(韩燕，2004；侯景儒，1993；孙洪泉，1990；阳正熙，2008)，因此勘查工作只要满足内蕴假设或者准平稳假设条件，即对于勘查工程要求同一矿体的见矿点在空间上大致均匀分布，样品数量要达到一定数量，样品品位分布满足正态分布、近似正态分布便可以进行变异函数的计算。

由于矿体成因的复杂性，有时控制矿体的样品品位分布不满足正态分布条件，因此需要进行正态变换。正态变换理论体系完备，常用的方法有对数变换、平方根变换、反正弦变换、倒数变换、多项式变换、Cox-Box变换、Johnson变换等(张维铭等，2000；王兆军， 2002；杨剑峰等，2006；李晓辉等，2010)。在变异函数计算时，可以根据变换结果对比选择变换方法，满足质量控制要求。

4 利用变异函数的变程进行资源量分类

4.1 样品品位的正态分布特征

服从正态分布的随机变量其概率密度函数为：

(1)

其中，μ位置参数，表示平均值；σ形状参数，表示标准差(汤大林，2004)。

当矿体内样品品位直方图满足正态分布特征时，其正态分布函数的位置参数μ等于样品的平均品位，形状参数σ等于品位的标准差；正态分布函数在μ±σ处存在拐点；在品位区间(μ-σ，μ+σ]内，样品品位接近矿体平均品位，方差小，分布概率为0.6826；在区间(μ-σ，μ+σ]外，样品品位远离平均值，方差大，分布概率为0.3174。

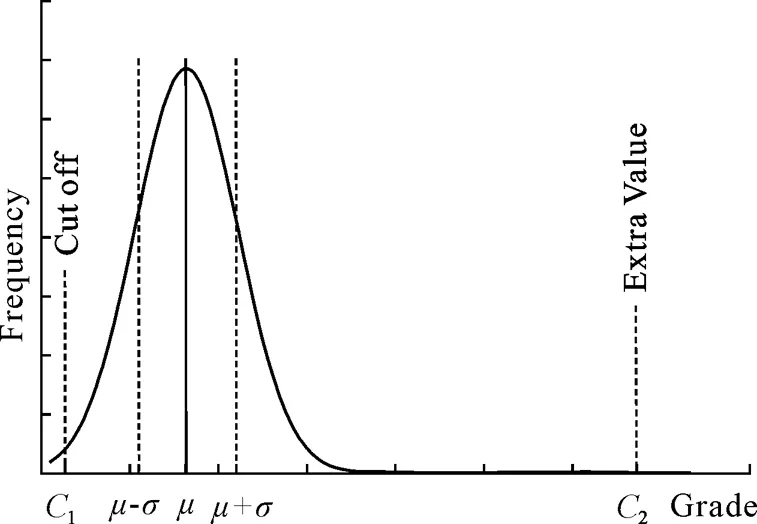
图1 服从正态分布的样品品位概率分布图Fig. 1 Diagram of probability density of sample grades in normal distribution

4.2 变异函数理论模型

对区域化变量进行结构分析本质上就是计算实验半变异函数γ*(h)，然后拟合理论半变异函数(简称变异函数)，并对其进行地质解释。实验半变异函数计算公式：

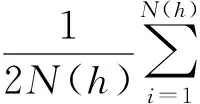
(2)

式中，h为滞后距，N(h)是滞后距为h时参加计算的样品个数，Z为空间上xi点的品位值。

由于实验半变异函数仅反映空间离散点的信息，无法反映空间离散点的内在规律，因此必须为其配以相应的理论模型以反映其内在关系和进行科学计算(侯景儒，1998；王家华，1993；阎辉，2002)。

球状模型变异函数γ(h)是地质统计学中最重要的理论变异函数模型，通过结构套合几乎可适应于各种类型的矿床。球状模型变异函数使用三参数进行定量描述，即变程a，块金方差C0，剩余方差C，C+C0为基台值，其值等于经典统计学中的总体方差σ2。其计算公式：

(3)

球状模型变异函数的特点是在原点处(h=0)的切线斜率为3C/2a，切线到达C值的距离为2a/3(张仁铎，2005)。

图2 球状变异函数理论模型Fig.2 Theoretic modal of spherical semi variogram

品位理论半变异函数模型一般通过实验半变异函数计算出的γ*(h)-h点对组成的离散点图形，使用球状模型变异函数，选择合适的结构及参数进行拟合完成。

4.3 变异函数与样品品位间的关系

变异函数是样品之间空间上相依性的度量，近距离的变异函数值比远距离的变异函数值作用大，反映样品间的相关性强(苏文汝， 2001；吴龙英，1992)。

当样品品位服从正态分布时，样品整体的方差σ2等于球状变异函数的基台值C+C0；分析实验半变异函数计算公式，位于区间(μ-σ,μ+σ]的样品总体决定了变异函数结构。决定了在[0，0.6826a]区间上变异函数先验方差较小的γ(h)部分；位于区间(μ-σ,μ+σ]外的样品影响着在(0.6826a，a]区间上变异函数先验方差较大的γ(h)部分；在区间[0，0.6826a]内的样品相关性大于在区间(0.6826a，a]内的样品相关性。

因此，服从正态分布的样品的两个拐点μ±σ处可作为样品相关性质变的分界点，在拐点之间即区间(μ-σ,μ+σ]，样品分布概率为0.6826，变异函数变程的0.6826倍(0.6826a)可作为划分控制资源量和推断资源量的分界点。

4.4 利用变程划分资源量类别的原则

变异函数的变程实际反映出的是最佳勘探工程间距。因此将工程间距等于变异函数变程的0.6826倍，使用了3个及以上工程的样品所估值的矿块划为控制资源量(332)。将工程间距等于变异函数变程的0.3413倍，使用了3个以上工程的样品所估值的矿块划为探明资源量(331)。将工程间距在变程内的工程所控制的所有其它单元划为推断资源量(333)。使用该方法，在进行矿体空块插值时，实际上同时对资源进行了分类。

5 影响资源量分类可靠性的主要因素

利用变异函数变程进行资源量分类其可靠程度主要受所建立的理论变异函数模型的稳健性影响(孙洪泉，1990；王仁铎，1988)，而影响理论变异函数稳健性的主要因素有以下几个方面：

(1) 样品取样间距和承载大小 随着取样间距的加大，样品变化的随机成分不断增加，矿体小型结构特征逐步被掩盖，而样品承载增加。同时随着样品承载的增加变异函数值随着减小，降低了变异函数对样品相关性的反映程度。因此在勘查阶段必须保证工程的合理分布和样品的承载。

(2) 计算实验半变异函数可靠性的距离和点对数目 G·马特隆的局部变异函数估计方差公式指出，估计方差与点对的数目有关，一般要求大于30～50对，变异函数滞后距(h)小于1/2研究区域(L)，即在这种条件下，推导出的变异函数才具有稳健性。

(3) 岩心采取率 岩心采取率对变异函数的影响程度与区域化变量的连续性相关，即和矿体矿化均匀程度相关。当矿化均匀时，岩心采取率对变异函数稳健性影响较小，当矿化不均匀时，岩心采取率对变异函数稳健性影响很大，变异函数可能无法反映矿体的真实变化规律。因此在勘查阶段必须保证采样质量。

(4) 特高品位 实验半变异函数是通过样品点对差值平方和计算得到的，因此特高品位对其影响强烈。当计算变异函数时，需要根据地质勘查规范要求处理特高品位。

(5) 混合效应 混合效应对实验变差函数所产生的影响较大。由于不同地质背景的影响，如不同的地质、构造单元，在矿床、矿体上由于不同的成因，成矿的多期次、多阶段，常使样品数据具有混合效应的特征。具有混合效应的样品数据其实验变差图离散程度高，所反映的结构特征偏离真实性，无法反映出矿体的变化特征。为避免这种非平稳性对实验变差函数的影响，应从地质因素着手，对具有混合效应的数据从地质上加以区分，分别处理。

6 应用对比

6.1 镍矿床概况

速佰益镍矿床位于印度尼西亚哈马黑拉岛，为一大型红土型镍矿床，主要产于超基性岩的红土风化壳中。该矿床的勘查工作参照《铜、铅、锌、银、镍、钼矿地质勘查规范》(DZ/T0214—2002，以下简称规范)标准执行。目前已勘探完毕，进入开发阶段。

其Ⅰ号矿体位于矿区北部西侧。矿体赋存标高为50～400m，其北、东、南边缘为水系分割，最西和南西为基岩分布区和辉长岩脉出露区。矿体平面形拟紧握的拳头，矿体产状与山坡基本一致，似层状缓倾沿山坡呈三至四个台阶分布。北部边缘地段为黄色、黄绿色碎块状腐岩出露区。

矿体北东、南西向长约2.0～2.4 km，北西南东向长约2.0 km，矿体面积达3.28 km2。有337个探矿工程控制，其中330个见矿，见矿率达98.0%。矿体厚1.0～35.0m，平均厚12.18m。单工程平均含镍1.07%～3.17%，平均1.67%，矿体平均含镍1.70%。

6.2 依据规范确定的资源量分类工程间距

Ⅰ号矿体镍品位变化系数为24.54，为均匀型，类型系数为0.6；厚度变化系数为59.11，为稳定型，类型系数为0.6；矿体形态中等，近似层状，缓倾斜，类型系数为0.4；矿体规模属于大型，类型系数为0.9；构造影响小，类型系数为0.3。类型系数总和为2.8，根据规范中红土型镍矿床勘探的相关要求，确定矿床勘探类型为Ⅰ类型。

按照规范中镍矿床勘探类型工程间距参考表(表1)，结合当地大量勘探开发镍矿的国际企业对红土型镍矿的地质勘查控制程度分类(一般采用50m×50m工程间距作为探明的资源量，100m×100m工程间距作为控制的资源量，200m×200m工程间距为推断的资源量)，最终选取50m×50m工程间距求获探明的内蕴经济的资源量(331)，100m×100m工程间距求获控制的内蕴经济的资源量(332)，200m×200m工程间距求获推断的内蕴经济的资源量(333)。

表1 镍矿床勘探类型工程间距参考表Table 1 Reference grid spacing values for surveys in nickel deposits

6.3 通过变异函数确定的资源量分类工程间距

速佰益Ⅰ号矿体内4189件样品镍品位-频率分布直方图(图3)显示,矿体样品平均品位为1.671，样品标准差σ为0.5893，样品品位分布近似正态分布，因此可以进行半变异函数拟合计算。

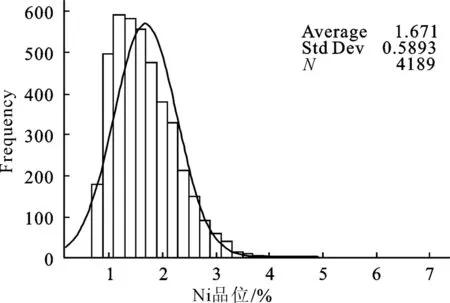
图3 Ⅰ号矿体样品品位-频率分布直方图Fig. 3 Histogram of nickel grade-frequency distribution of samples in No.Ⅰorebody

利用Micromine 2013矿业软件通过实验半变异函数对样品点进行全方向空间点对计算，采用球状半变异函数进行拟合，取得全向半变异函数参数。计算结果表明(图4)：块金方差C0=0.073，剩余方差C=0.282，基台值S=0.355，拟合的变程a=156m，严格意义上的变程a=148.2m。

图4 Ⅰ号矿体理论变异函数模型Fig. 4 Spherical model of semi variogram of No.Ⅰorebody

利用半变异函数变程计算资源量分类的控制工程间距：

探明资源量Dmea=0.3213a=50.6m；

控制资源量Dind=0.6826a=101.2m；

推断资源量Dinf=a=148.2m；

因此，确定划分探明资源量的工程间距为50.6m；控制资源量的工程间距为101.2m；推断资源量的工程间距为148.2m。

6.4 规范和变异函数确定的分类工程间距比较

比较地质勘查规范(DZ/T0214—2002)要求确定的资源量分类工程间距与利用半变异函数的变程所确定的工程间距，可以看出二者基本一致，对于推断资源量存在明显差异，利用变异函数变程确定的分类工程间距更可靠，但二者均与规范中的参考工程间距有一定的差距。从确定过程看，依据规范确定资源量分类工程间距，需要先明确勘探类型，然后选择参考工程间距，整个过程技术人员的主观性很大，甚至有时很难把控，例如对于勘探类型相同的红土型镍矿床，按照规范，其资源量分类参考工程间距应该相同，但由于成矿环境的差异，可能其资源量分类的工程间距会有很大的差异，依据规范很难做出选择。有时为了确定的工程间距更可靠、更接近实际，最终的结果可能和规范冲突。对于利用半变异函数变程来确定资源分类的工程间距就不存在上述问题，只要满足前文讨论过的条件和应注意的问题，便可以可靠地计算出符合各矿床差异化的资源量分类的工程间距。

7 总结

(1) 对矿产资源量进行地质分类，目的是确定资源量的可靠程度。

(2) 利用变异函数变程划分资源量类别是通过控制样品品位空间位置上的相关性决定资源可靠程度的方法，是建立在变异函数理论基础上的定量划分方法。

(3) 通过变异函数变程可以为不同的矿床确定适合自身特征的划分资源量类别的工程间距。

(4) 在利用变异函数变程划分资源类别时需要重视研究影响变异函数稳健性的因素。

Han Yan, Xia Li-xian, Xiao Ke-yan. 2004. Dual model of universal Cokriging[J]. Progress in Geophisics, 8(2): 205-207(in Chinese with English abstract)

Hou Jing-ru, Huang Jing-xian. 1994. Analysis and application of Non-parametric and multivariate geostatistics theories[M]. Beijing: Metallurgical Industry Press: 39-41, 66-69(in Chinese)

Hou Jing-ru, Huang Jing-xiang. 1993. Geostatistic principle and method[M]. Beijing: Metallurgical Industry Press: 86-87(in Chinese)

Hou Jing-ru. 1998. Applied Geostatistics[M]. Beijing: Geological Pulishing House: 31-60(in Chinese)

Li Shou-yi, Ye Song-qing. 2008. Geology of mineral exploration [M]. Beijing: Geological Publishing House: 183-189(in Chinese)

Li Shou-yi, Ye Song-qing. 2008. Geology of mineral exploration [M]. Beijing: Geological Publishing House: 183-189(in Chinese)

Li Xiao-hui, Yuan Feng, Bai Xiao-yu, Zhang Ming-ming, Jia Cai, Zhou Hai-fa. 2010. Comparison of normalization methods for non normal distributed soil elements data in typical mining area[J]. Geography and Geo-Information Science, 26(6): 102-105(in Chinese with English abstract)

Li Zhong-xue, Li Cui Ping, Li Cun-min, Seng De-wen, Yu Dong-ming. 2007. Visualization techniques for geology and mining systems[M]. Beijing: Science Press: 80-93(in Chinese)

Su Wen-ru. 2001. The application of variable functions to prospecting net determination for No.X Orebody of Dachang Tin Mine, Guangxi Province[J]. Mineral and Geology, 15(6): 755-758(in Chinese with English abstract)

Sun Hong-quan. 1990. Geostatisics and its applications[M]. Beijing: China University of Mining and Technology Press: 39-41, 66-69(in Chinese)

Tang Da-lin, Zhang Yu-huan, Chen Su-min, Wang Jing. 2004. Probability and statistics[M]. Tianjin: Tianjing University Press: 169-183(in Chinese)

Wang Jia-hua, Gao Hai-yu. 1993. Linear combination problem of linear Kringing and its dual form[J]. Journal of Xi’an Petrolium Institute, 7(3): 63-65(in Chinese with English abstract)

Wang Ren-duo, Hu Guang-dao. 1988. Linear geostatistics [M]. Beijing: Geological Pubilishing House: 57-58(in Chinese)

Wang Zhao-jun. 2002. Design theory of dynamic quality control chart[J]. Chinese Journal of Applied Probability and Statistics, 18(3): 316-331(in Chinese)

Wu Long-ying. 1992. Geostatistics study on changes in nature and extent for geological body[J]. Geology and Exploration, 28(1): 36-42(in Chinese with English abstract)

Yan Hui, Zhang Xue-gong, Ma Yun-qian, Li Yan-da. 2002. The parameter estimation of RBF kernel function based on variogram[J]. Acta Automatica Sinica, 28(3) : 120-126(in Chinese with English abstract)

Yang Jian-feng, Liu Yu-mi, He Jin-feng. 2006. Process capability analysis in non-normality based on box-cox power transformatio[J]. Systems Engineering,24(8): 102-196(in Chinese with English abstract)

Yang Zheng-xi, Wu Qian-hong, Peng Zhen-xing, Yan Bing. 2008. Geoscience data analysis tutoral[M]. Beijing:Scientifical & Technical Publishing House:170-177(in Chinese)

Yang Zheng-xi. 2006. Mineral resources exploration[M]. Beijing: Science Press:210-234(in Chinese)

Zhang Ren-duo. 2005. Spatial variability theory and its application[M]. Beijing: Science & Technology Publishing House: 39-41, 66-69(in Chinese)

Zhang Wei-ming, Shi Xue-zhong, Lou Long-xiang. 2000. Technique for transforming non-normal data to normality[J]. Journal of Zhejiang Institute of Science and Technology, 17(3): 204-207(in Chinese with English abstract)

[附中文参考文献]

韩 燕, 夏立显, 肖克炎. 2004. 泛协克里金的对偶形式[J]. 地球物理学进展, 8(2): 205-207

侯景儒, 黄竞先. 1993. 地质统计学的理论与方法[M]. 北京:冶金工业出版社: 86-87

侯景儒, 黄竞先. 1994. 非参数及多元地质统计学的理论分析及其应用[M]. 北京: 冶金工业出版社: 39-41, 66-69

侯景儒. 1998. 实用地质统计学[M]. 北京: 地质出版社: 31-60

李守义, 叶松青. 2003. 矿产勘查学[M]. 北京: 地质出版社: 183-189

李晓辉, 袁 峰, 白晓宇, 张明明, 贾 蔡, 周涛发. 2010. 典型矿区非正态分布土壤元素数据的正态变换方法对比研究[J]. 地理与地理信息科学, 26(1): 102-105

李仲学, 李翠平, 李春民, 僧德文, 余东明. 2007. 地矿工程三维可视化技术[M]. 北京: 科学出版社: 80-93

苏文汝, 2001. 变异函数在确定广西大厂锡矿X号矿体网度中的应用[J]. 矿产与地质, 15(6): 755-758

孙洪泉. 1990. 地质统计学及其应用[M]. 北京: 中国矿业大学出版社: 39-41, 66-69

汤大林, 张玉环, 陈淑敏,王 菁. 2004. 概率论与数理统计[M]. 天津: 天津大学出版社: 169-183

王家华, 高海余. 1993. 线性克里金的线性组合问题及其对偶形[J]. 西安石油学院学报, 7(3): 63-65.

王仁铎, 胡光道. 1988. 线性地质统计学[M]. 北京: 地质出版社: 57-58

王兆军. 2002. 关于动态质量控制图的设计理论[J]. 应用概率统计, 18(3): 316-331

吴龙英. 1992. 地质体变化性质与变化程度的地质统计学研究[J]. 地质与勘探, 28 (1): 36-42

阎 辉, 张学工, 马云潜, 李衍达. 2002. 基于变异函数的径向基核函数参数估计[J]. 自动化学报, 28(3), 120-126

阳正熙, 吴堑虹, 彭真兴, 严 冰. 2008. 地学数据分析教程[M]. 北京: 科学技术出版社: 170-177

阳正熙. 2006. 矿产资源勘查学[M]. 北京: 科学出版社: 210-234

杨剑峰, 刘玉敏, 贺金凤. 2006. 基于Box-Cox幂转换模型的非正态过程能力分析[J]. 系统工程, 24(8): 102-106

张仁铎. 2005. 空间变异理论及应用[M]. 北京: 科学技术出版社: 39-41, 66-69

张维铭, 施雪忠, 楼龙翔. 2000. 非正态数据变换为正态数据的方法[J]. 浙江工程学院学报, 17(3): 204-207

A Method of Determining Grid Spacing in Surveys for Classification of Mineral Reserves

GAO Hang-xiao1, REN Xiao-hua1, GUO Jian2

(1. Northwest Nonferrous Metal Geology and Exploration Bureau, Xian, Shaanxi 710068; 2. Institute of Mineral Resources Research, China Metallurgical Bureau, Beijing 100025)

The relevant geological specifications at home and abroad generally contain a definition of classification of mineral reserves, but no a quantitative method of determining grid spacing in surveys for classification, frequently leading to potential quality problems in exploration work. This paper addresses this issue using the model of the variogram and statistics. A range of semi variogram represents varying degrees of interdependency of regional variables. When sample grades show a normal distribution, average grade equals the position parameter μ of normal distribution, grade standard deviation equals shape parameter σ, and grade variance equals the base value of semi variogram. Sample distribution probability is 0.6826 in (μ-σ, μ+σ] of the inflection point, and 0.6826 times (0.6826a) of the range of semi variogram can be used as the standard survey spacing of classification of indicated mineral reserves. The main factor affecting the reliability of classification of mineral reserves is the robustness of the theoretical model of semi variogram established.

mineral reserves, classification, grid spacing in surveys, semi variogram, normal distribution

2013-10-31；

2014-01-20；[责任编辑]郝情情。

高航校(1969年—)，男，2007年毕业于澳门城市大学，获硕士学位，高级工程师，长期从事固体矿产地质勘查与技术研究工作。E-mail：gaohangxiao@gmail.com。

P618

A

0495-5331(2014)02-0340-6