基于粗糙集理论的社区体育服务公众满意度评价实证研究

陈 旸，左 珊

(湘潭大学 体育教学部，湖南 湘潭 411105;湘潭大学 公共管理学院，湖南 湘潭 411105)

基于粗糙集理论的社区体育服务公众满意度评价实证研究

陈 旸，左 珊

(湘潭大学 体育教学部，湖南 湘潭 411105;湘潭大学 公共管理学院，湖南 湘潭 411105)

通过理论研究和公众参与调查，构建出了一套基于公众参与视角的社区体育服务公众满意度评价指标体系。考虑到实际应用中，待评价对象数据规模通常较少的问题，引入粗糙集理论建立了基于信息熵观点下的社区体育服务公众满意度智能评价模型，该模型在利用粗糙集方法客观确定指标权重时，将决策表进行合理分块划分，以层次式计算的方式来逐步实现对各个二级指标权重的客观求取，为小样本数据问题粗糙集求解提供了一个全新的解决方案。通过实证研究，验证了评价指标体系的合理性和粗糙集智能评价模型的有效性与优越性。

社区体育服务；粗糙集理论；评价指标体系；指标权重

党的十八大报告中强调指出：“推动文化产业快速发展，让人民精神文化生活更加丰富多彩……全民健身要取得新成绩。”随着全面建成小康社会，推进社区文化建设发展进程的逐渐深入，社区体育文化作为重要的社区文化建设内容，国家给予了越来越多的重视，为社区体育建设的发展指明了方向。社区体育服务是政府部门积极推进社区体育建设的一项重要内容，是推进社会主义先进文化建设、引领社区居民和社区单位紧密联系的重要环节，在满足社区居民体育需求方面发挥着重要的作用。社区体育服务公众满意度是指社区居民对社区体育服务的满意程度，是社区居民将其对社区体育服务的期望与社区体育实际提供的服务相比较后得出的一个对社区体育服务的评价，是社区居民在接受社区体育一次或多次服务后的内心感受和主观评价[1]634-638。为了检验社区体育服务建设的实际成果，就需要对社区体育服务公众满意度情况进行科学评价，“以评促建”，“以评促改”，达到提升社区体育服务公众满意度的目的。

通过梳理与社区体育服务公众满意度评价相关的研究可以发现：何颖运用文献资料法、问卷调查法、访谈法和数理统计方法，依据系统论、社会评价理论、社会体育学理论和心理学理论建立了一套城市社区体育服务满意度测评模型并进行了实证研究[2]40-42；马葛生引入了基于期望值的模糊多属性决策方法构建了社区体育服务居民满意度测评体系[3]53-58；其他相关的研究主要集中在社区体育实践调查方面[4]39-42，[5]1009-1013。总的来说，鉴于社区体育服务公众满意度的重要性，其近年来越来越受到学者们的广泛关注，然而对社区体育服务公众满意度评价的智能化研究相对较少。

基于已有的研究成果，通过公众参与调查的方式，尝试建立一套社区体育服务公众满意度评价指标体系。研究社区体育服务公众满意度评价，不仅需要构建科学的评价指标体系而且还需要有针对性地选取合理的定量化评价方法。粗糙集理论是Z.Pawlak[6]341-356提出的一种数据推理方法，其具有不依赖样本数据之外的先验知识而真实反映数据本身所隐藏的信息，得到问题的内在规律的独特优势[7]233-246。文章将粗糙集理论引入到社区体育服务公众满意度评价中,尝试构建一种智能化定量获取指标权重的层次式计算新算法，从而实现基于粗糙集理论的社区体育服务公众满意度合理评价分析，为社区体育服务公众满意度研究提供更为合理客观的评价结论。

一、社区体育服务公众满意度评价指标体系构建

(一)构建社区体育服务公众满意度评价指标体系的原则

1. 比较性和完整性。构建社区体育服务公众满意度评价指标体系时尽可能采用相对指标,便于不同对象之间进行比较。但为了反映对象之间规模上的差异,也应选取一些绝对指标。另外,各个指标的计量范围、口径必须一致,才能对社区体育服务公众满意度情况进行综合比较。做到全面不容易,要求所选的指标能够是一个有机整体,考虑到影响社区居民满意度的因素,而且指标间的相互配合能比较科学、准确地涵盖评价所需的基本内容。

2. 引导性和可行性。社区体育服务公众满意度评价指标体系的设置和评价的实施,目的是要对公众起到引导和导向的作用。通过指标的设置和评价,引导公众识别信息、认识信息,从而提高公众的信息搜集、检索、处理、使用的能力，并提升社区体育服务的质量和增加公众获得的利益。所需的社区体育服务公众满意度评价指标原则上从现有的统计指标中产生,少量需重新计算和统计的指标也应尽可能地在现有统计数据的基础上取得。

3. 理论实践结合，定量定性结合。社区体育服务公众满意度评价指标体系构建是一项复杂的系统工程，应从公众的实际需求向实际应用转变，通过理论研究与走访调查相结合的方式才可能获得较为合理的解决方案。同时由于社区体育服务公众满意度评价指标体系研究的特殊性和先进性，在研究分析过程中，采用定量计算和定性分析相结合的手段，对指标体系内涵予以多层面、精细化的丰富，更好地为提高社区体育服务的质量提供实际可行的决策服务。

(二)社区体育服务公众满意度评价指标体系设计

本文通过大量借鉴社区体育服务的研究成果[8]55-59，[9]25-30，[10]19-22,30，考虑到现实数据的可获得性和构建社区体育服务公众满意度评价指标体系的三条原则，经过理论层面上的深入剖析，我们拟从体育基础设施、体育服务活动、体育服务人员三个方面搭建体育服务公众满意度评价指标体系。

据此，我们选取出了包括体育服务项目数、体育服务机构数、年体育服务经费投入、人均体育活动面积、基础设施建设情况、年体育锻炼活动数、年运动康复服务活动数、年体育竞赛服务活动数、年体育信息服务活动数、服务人员学历结构、服务人员年培训次数、服务人员业务考核通过率、体育服务指导员数量共13个二级指标。为了使得该评价指标体系更加符合公众的需求和社区体育服务的发展，有利于提升公众参与下的社区体育服务质量，将初建的社区体育服务公众满意度评价指标体系进行问卷调查。问卷共涉及16个单项选择题，主要是对初建的社区体育服务公众满意度评价指标体系进行满意度调查，包括“1.满意”、“2.不满意”、“3.说不清”。调查对象面向公众、社区居民等，共发放问卷200份，共回收问卷192份，最终确定180份有效问卷。所得到的反馈统计结果如图1所示。

图1 公众参与下的社区体育服务公众满意度评价指标体系问卷调查结果

对问卷调查的结果进行统计和分析，保留赞成率60%以上的指标，去除赞成率60%以下的指标(如：基础设施建设情况、年体育锻炼活动数、服务人员学历结构)。最终汇总得到在公众参与下的社区体育服务公众满意度评价指标体系，如表1所示。

表1 社区体育服务公众满意度评价指标体系

一级指标二级指标指标详情体育服务项目数(个)C11社区体育服务项目的总数体育基础设施C1体育服务机构数(个)C12社区体育服务机构的总数人均体育活动面积(平方米/人)C13社区居民平均体育活动的范围、面积年体育服务经费投入(万元/年)C14社区一年内对体育服务的资金投入量大小年体育竞赛服务活动数(个/年)C21社区一年内开展体育竞赛服务活动的总数体育服务活动C2年运动康复服务活动数(个/年)C22社区一年内开展运动康复服务活动的总数年体育信息服务活动数(个/年)C23社区一年内开展体育信息服务活动的总数服务人员年培训次数(次/年)C31社区体育服务人员一年内参加的培训次数体育服务人员C3服务人员业务考核通过率(%)C32社区体育服务人员业务考核情况体育服务指导员数量(个)C33社区内拥有的体育服务指导员的数量

二、基于粗糙集理论的社区体育服务公众满意度智能评价模型

(一)粗糙集基本理论

定义2[12]154-156：给定决策表S，若有B⊆A，则定义属性集B上的不可分辨关系IND(B)为：

IND(B)={(ui,uj)∈U2|∀b∈B,f(ui,b)=f(uj,b)

定义3[13]157-165：在决策表S中，∀X⊆U且X≠φ,则定义集合X在属性集B⊆A上的下近似划分集B*(X)和上近似划分集B*(X)为：

B*(X)={ui∈U|[ui]B⊆X}; B*(X)={ui∈U|[ui]B∩X≠φ};

其中[ui]B={uj|(ui,uj)∈IND(B)}，B*(X)也称为X的B正域，记作：PosB(X)

定义4[12]154-156：在决策表S中，若有B⊆C,Y∈U/IND(D)，则决策属性D的B正域PosB(D)定义为：

定义5[14]238-241：在决策表中，若U/IND(C)={X1,X2,…,Xq},U/IND(D)={Y1,Y2,…,YP},则对象集U在条件属性集C下相对于决策属性D划分的信息熵定义为：

其中Card(*)表示集合的基数。

定义6[14]238-241：在决策表S中，定义属性c∈C粗糙集信息熵意义下的重要度为：

SGF(c)=I(D|C)-I(D|C-{c})

(二)社区体育服务公众满意度评价决策分析算法

考虑到针对社区体育服务公众满意度评价决策分析的实际应用背景，评价指标体系包含一级指标条件属性集和二级指标条件属性集，我们下面将定义1中在决策表S内的条件属性集(指标集)C进行如下更为细致的描述：

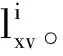
图2 社区体育服务公众满意度评价步骤

通过图2的描述，基于粗糙集的社区体育服务公众满意度评价决策分析具体实现步骤如下：

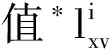
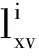
-min(lxv))

(1)

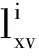
-low(lxv))

(2)

其中，max(lxv)为原始数据集中，在属性cxv下的最大数据取值；min(lxv)为原始数据集中，在属性cxv下的最小数据取值，high(lxv)为成本型属性中不允许值的上限；low(lxv)为效益型属性中不允许值的下限。

2. 连续型数据离散化。由于粗糙集只能处理离散化的数据，因此，需要对连续型数据进行离散化处理，本文采取的是等距离法[14]238-241。具体步骤如下：

1)属性cxv在离散化时的取值区间长度计算为：

(3)

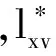
2)对于对象ui，在属性cxv下的离散化结果计算为：

(4)

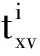
3. 构建决策表。把数据离散化的结果转化成为决策表S=(U,A,V,f)，U={u1,u2,…un}表示各个社区的集合，条件属性评价指标集C={C1,C2,…CZ}，其中Cx(x=1,2,…,z)为一级指标条件属性，该一级指标条件属性包含若干二级指标条件属性，可以描述为Cx={cx1,cx2,…,cxv}，决策属性集D={y1,y2,…,yr}。

4. 客观权重确定。通过把基于信息熵观点下的粗糙集计算方法引入社区体育服务公众满意度智能评价分析中，不依赖任何的先验知识，获取属性(也即指标)的客观权重。此外，考虑在实际的社区体育服务公众满意度评价应用中，待评价的社区对象数据规模通常较少，而相应的评价分析指标数目较多，因此在利用粗糙集方法客观计算评价指标权重时，考虑基于一级指标集进行分块划分，以层次式计算的方式来逐步实现对各个二级指标权重的客观求取，为小样本数据问题粗糙集求解提供了一个全新的解决方案。

在信息熵观点下，粗糙集运算直观性较强，不同属性的重要性可以基于信息熵的运算得到相应的定量化数值。即通过从决策表中剔除某条件属性，再考察在该属性缺失的情况下整个决策分类信息熵的变化情况。如果剔除后变化较大，则说明该属性重要性大；反之，重要性小。

算法1：局部分块下的二级指标条件属性权重计算

输入：决策表S=(U,A,V,f)

输出：各一级指标下的二级指标条件属性权重值w。

Step1. 获得全体对象集在一级指标Cx分块下的划分结果U/IND(Cx)，在决策属性D上的划分结果U/IND(D)，以及在每次剔除一级指标Cx下的条件属性cxv后的划分结果U/IND(CX-{cxv});

Step2. 计算一级指标Cx上的划分相对决策属性D上的划分的信息熵I(D|Cx)；在依次剔除一级指标Cx下的各个条件属性cxv后,计算Cx-{cxv}上的划分相对决策属性D上的划分的信息熵I(D|Cx-{cxv})；

Step3.计算一级指标Cx分块下的各个条件cxv粗糙集意义下的重要度：

SGF({cxv})=I(D|Cx)-I(D|Cx-{cxv});

Step4. 计算一级指标Cx局部分块下的各个二级指标条件属性cxv的权重值：

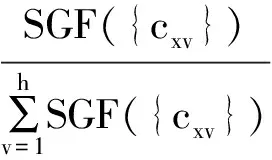
算法2：各一级指标的权重计算

输入：决策表S=(U,A,V,f)

输出：各一级指标的权重值w

Step1. 获得全体对象集U在条件属性集C上的划分结果U/IND(C)，在决策属性D上的划分结果U/IND(D)，以及在每次剔除条件属性集C下的一级指标Cx后的划分结果U/IND(C-Cx)；

Step2. 计算条件属性集C上的划分相对决策属性D上划分的信息熵I(D|C)，以及在依次剔除一级指标Cx后，计算条件属性集C-Cx上的划分相对决策属性D上的划分的信息熵I(D|C-Cx)，其中Cx∈C；

Step3. 计算各一级指标Cx在粗糙集意义下的重要度：SGF(Cx)=I(D|C)-I(D|C-Cx)；

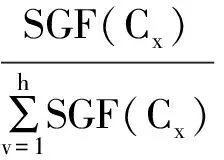
算法3：待评价对象的综合评价值

输入：决策表S=(U,A,V,f)，局部分块下的二级指标权重w(cxv)和一级指标权重w(Cx)

输出：待评价对象ui∈U的综合评价值Ki

Step1. 计算全局意义下的二级指标最终权重值：

Step2. 计算评价对象的社区体育服务公众满意度评价结果：

三、实证分析

本研究对湖南省长株潭城市群中的十个具有代表性的社区进行了实地调查，其中长沙4个社区(砂子塘社区、白沙社区、桔园社区、金地社区)，株洲3个社区(七斗重社区、文化路社区、王塔冲社区)，湘潭3个社区(纯冲塘社区、湘潭大学社区、霞光社区)，共发放问卷500份，回收有效问卷456份，问卷有效回收率为91.2%；并对这十个社区的领导进行访谈，根据指标体系构建的情况针对性地收集了相关数据，基于收集的相关数据对本文所提出的评价指标体系和相应的智能评价算法模型予以验证与分析。

1. 数据采集和预处理。10个待评价的社区记为U={u1,u2,u3,u4,u5,u6,u7,u8,u9,u10}，所有指标的相关数据如表2斜杠前所示。确定指标的不允许值如表2所示，对于成本型属性，不允许值是指现实正常情况下不能接受的最大值；对于效益型属性，不允许值是指现实正常情况下不能接受的最小值。10个二级指标均属于效益型指标，利用公式(2)计算各指标的得分，指标得分如表2斜杠后所示。本文将“公众的满意度情况”作为考核社区体育服务质量的一个表征，作为决策属性D，公众分别根据自己的客观感受对这10个社区的体育服务质量的满意度情况进行打分，100分表示非常满意，0分表示非常不满意，打分结果取平均值，如表2所示。

2. 连续型数据离散化。把所有指标均分为3个等级，利用公式(3)确定各个指标的离散区间；根据公式(4)确定各个指标的离散化结果，如表3所示。

3. 构建决策表。将16个二级指标作为决策表中的条件属性集C；将“公众的满意度情况”作为决策属性D，见表3。

4. 客观权重确定。本文首先以“体育基础设施”一级指标为例，将决策表进行分块，并基于信息熵观点下的粗糙集方法求取“体育基础设施”下的局部分块二级指标权重。由此，将表3所示的决策表进行分块提取，获得如表4所示的“体育基础设施”一级指标下的局部分块决策表。

由表4，根据算法1可得：

w(c11)=0.296,w(c12)=0.296,

w(c13)=0.408,w(c14)=0。

同理，分别以“体育服务活动”、“体育服务人员”这两个一级指标将决策表进行分块，并基于信息熵观点下的粗糙集方法求取“体育服务活动”、“体育服务人员”各自局部分块下的二级指标权重。

可得：

w(c21)=0.333,w(c22)=0.334,

w(c23)=0.333,w(c31)=0.296,

w(c32)=0.296,w(c33)=0.408。

根据以上的结果分析，社区体育服务公众满意度评价指标体系下的年体育服务经费投入为冗余属性，应去除这个冗余属性；二级指标中人均体育活动面积、年运动康复服务活动数以及体育服务指导员数量分别在各自的一级指标下重要性最高。

然后在决策表中分别剔除一级指标“体育基础设施”、“体育服务活动”、“体育服务人员”下的所有二级指标，并基于信息熵观点下的粗糙集方法求取各一级指标的权重。由表3，根据算法2可得：

w(C1)=0.333,w(C2)=0.333,w(C3)=0.334

最后把一级指标下获得的局部分块下的二级指标权重与一级指标权重进行融合，得到全局意义下的各个二级指标最终权重值，根据算法3可得： w*(c11)=0.099,w*(c12)=0.099,w*(c13)=0.136 w*(c21)=0.111,w*(c22)=0.111,w*(c23)=0.111 w*(c31)=0.099,w*(c32)=0.099,w*(c33)=0.136

根据以上的粗糙集智能化分析结果，在社区体育服务公众满意度评价分析中，我们应重点关注社区居民的体育活动场地、社区提供的体育服务活动的开展、社区体育服务指导员等方面的考量因素。

最终，我们容易求得10个待评价社区的社区体育服务公众满意度综合评价值分别为： K1=69.463,K2=68.011,K3=67.039,K4=50.993 K5=66.898,K6=79.054,K7=63.943,K8=61.321 K9=69.026,K10=68.823。

为了进一步验证本文方法的合理性和优越性，特将本文方法与文献[16]61-65中所提出的方法基于本文的数据进行对比计算分析。

采用文献[16]61-65中的方法对本文社区体育服务公众满意度数据进行评价，并对综合评价结果进行排序，如表5所示。

从所得的评价结果中可以看出，两种方法计算得到的各个社区的评价值排序相差不大。为了进一步验证本文模型的合理有效性，特定义评价决策方案区分度为：

(5)

其中n为待评价社区的数目。

区分度越大意味着待评价社区间的优势可分辨性越大，也直接表明该评价方法的优越性。通过公式(5)计算上述两种社区体育服务公众满意度评价方法下的方案间的区分度，如表5所示，本文方法的评价决策方案区分度更大，表明本文方法更具一定的优越性，也表明了本文模型的合理有效。

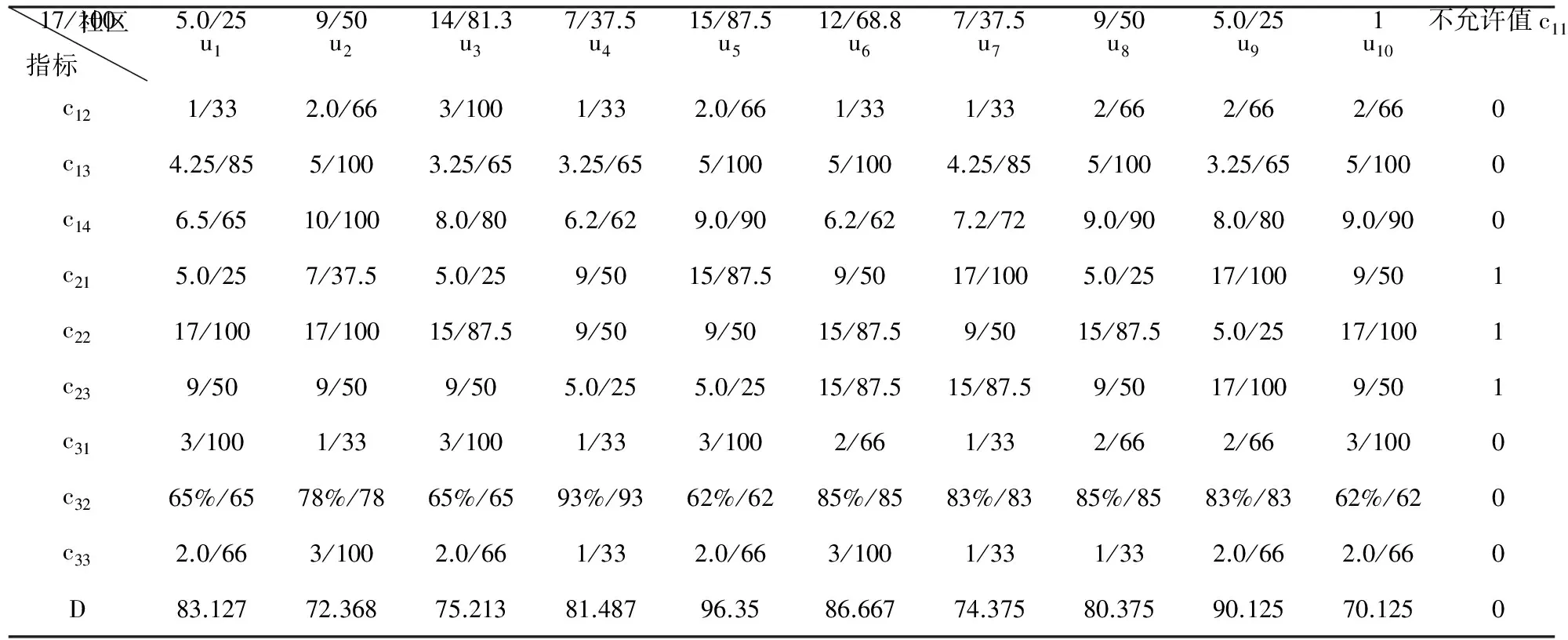
表2 10个社区在指标集下的原始数据

表3 数据离散化后的决策表

表4 “体育基础设施”一级指标下的局部分块决策表

表5 两种方法计算的评价值结果及排序

四、结语

本文通过理论研究和公众参与调查，构建了一套基于公众参与下的社区体育服务公众满意度评价指标体系。把粗糙集方法引入社区体育服务公众满意度评价分析中，在已有的研究基础上建立了基于粗糙集理论的社区体育服务公众满意度智能评价模型。同时考虑到实际社区体育服务公众满意度评价分析中小样本数据的特点，创新性地将评价决策表进行分块解构，利用信息熵观点下的粗糙集方法基于层次式的计算途径，客观获取各评价指标的权重值，为后续的综合评价分析奠定基础，这种求解方法无需依赖于专家的经验，具有严密的逻辑推理和理论依据。实证表明，该粗糙集智能评价模型是切实可行、有效的，为社区体育服务公众满意度评价提供了新的智能化评价方法。当然，由于社区体育服务公众满意度的复杂性，该评价指标体系还不够全面、深入等，这些问题有待进一步研究。

[1]邹凯,马葛生,苏鹏.基于LISREL的社区服务公众满意度测评研究[J].中国管理科学,2008, 16(10).

[2]何颖,徐明.城市社区体育服务满意度测评模型的理论和实证研究[J].武汉体育学院学报, 2007,41(11).

[3]陈旸,马葛生.基于模糊多属性决策的社区体育服务公众满意度测评研究[J].湘潭大学学报(哲学社会科学版),2010(5).

[4]黄波,李薇.广州市荔湾区社区体育服务的调查与分析[J].体育学刊,2007,14(4).

[5]王凯珍.中国城市不同类型社区居民体育活动现状的调查研究[J].北京体育大学学报,2005, 28(8).

[6]Z. Pawlak. Rough sets[J]. International Journal of Information and Computer Science, 1982(11).

[7]Yee Leung, Manfred M. Fischer, Wei-Zhi Wu, Ju-Sheng Mi. A Rough Set Approach for the Discovery of Classification Rules in Interval-valued Information Systems[J]. International Journal of Approximate Reasoning, 2008,5(2).

[8]张俊伟,苗苗,郑卫民.新农村建设中农村社区体育服务体系构建的发展模式探析[J].体育与科学,2011,32(1).

[9]李丽清,刘卫东.基于粗糙集的患者满意度评价模型及其实证分析[J].数学的实践与认识,2009, 14(39).

[10]丁鸿祥.社区公共体育服务供给模式创新研究[J].广州体育学院学报,2012,32(1).

[11]朱红灿,陈能华.基于距离辅助粗糙集的政府信息公开公众满意度评价模型[J].情报杂志, 2010,29(8).

[12]朱红灿,陈能华.粗糙集条件信息熵权重确定方法的改进[J].统计与决策,2011(8).

[13]谭旭,唐云岚,陈英武.基于粗糙集的区间型数据离散化算法[J].系统工程理论与实践, 2009,29(6).

[14]高维春,谭旭.决策属性未知下的学生评教粗糙集分析[J].计算机工程与应用,2012,48(9).

[15]岳超源.决策理论与方法[M].北京:科学出版社,2006.

[16]周志远,沈固朝.粗糙集理论在情报分析指标权重确定中的应用[J].情报理论与实践,2012, 35(9).

责任编辑：熊先兰

Based on Rough Set Theory of Community Sports Service Public Satisfaction Evaluation of Empirical Study

CHEN Yang，ZUO Shan

(Department of Physical Education, Xiangtan University, Xiangtan, Hunan 411105; School of Public Administration, Xiangtan University, Xiangtan, Hunan 411005, China)

This paper attempts to establish an evaluation index system of community sports service public satisfaction, which based on document research and public investigation.In addtion,considering the practical application, stay evaluation object data size is usually less of a problem, introduced rough set theory based on information entropy under the view of community sports service public satisfaction intelligent evaluation model. According to the practical problem of evaluation index system of each evaluation index weight gain with small sample data, we try to divide the decision table into small blocks and use hierarchical way to get the objective to calculate the weight of each evaluation index, which based on rough set theory. At the end of the article, empirical analysis proved that the evaluation index system takes on rationality and the rough set of intelligent evaluation model takes on effectiveness and superiority. Keywords：community sports service；rough set theory；evaluation index system；index weight

2013-09-21

陈旸(1972-)，男，湖南湘潭人，湘潭大学公共管理学院教授，硕士生导师。

G812.4；TP18

A

1001-5981(2014)01-0095-07