对称布尔函数算术Walsh变换的快速算法
赵庆兰, 郑 东,2
(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121;2.西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)
对称布尔函数算术Walsh变换的快速算法
赵庆兰1, 郑 东1,2
(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121;2.西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)
为了提高对称布尔函数算术Walsh变换的实现效率,利用Krawtchouk 多项式研究对称布尔函数的算术Walsh变换。根据算术Walsh变换的定义讨论对称布尔函数的算术 Walsh变换和Krawtchouk 多项式之间的关系,给出并证明基于Krawtchouk 多项式描述的对称布尔函数的算术 Walsh变换的简约表达式。利用得出的简约表达式和Krawtchouk 多项式的性质即可得出一种实现对称布尔函数的算术 Walsh变换的快速算法,该算法具有较低的时间复杂度和空间复杂度。
布尔函数;Walsh变换;2-adic数;Krawtchouk多项式
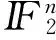
对称布尔函数是一类特殊的布尔函数,它的输出函数值只与输入向量的汉明重量有关,正是由于这个特殊的性质,对称布尔函数在软件硬件实现方面能够使计算复杂度降低,具有广泛的应用,因而受到研究者的关注[8-10]。对称布尔函数的经典的Walsh谱是一个对称实值函数,并且在具有相同汉明重量的向量点具有相同的Walsh变换系数[11]。文献[12]利用文献[5]中的定理2证明了对称布尔函数的算术Walsh谱是对称实值函数。Krawtchouk多项式是描述对称布尔函数的经典Walsh变换的重要工具,本文利用Krawtchouk多项式研究对称布尔函数的算术Walsh谱,并利用Krawtchouk多项式的特殊性质给出了基于Krawtchouk多项式的对称布尔函数的算术Walsh谱的简约表达式。
目前尚无文献讨论对称布尔函数的算术Walsh谱的实现算法,本文借鉴文献[10]中提出的一种对称布尔函数的经典Walsh谱的实现算法,利用基于Krawtchouk多项式的对称布尔函数的算术Walsh谱的简约表达式和Krawtchouk多项式的性质,提出了一种计算对称布尔函数的算术Walsh谱的快速实现算法,该算法在实现过程中利用Krawtchouk多项式的性质减少了计算量,该算法的时间复杂度是O(n2),空间复杂度是O(n)。
1 基础知识
定义1 令n为正整数,n元布尔函数的定义为
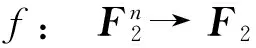
其中IF2={0,1}。记Bn为全体n元布尔函数的集合,且
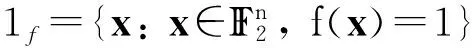
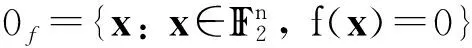
f的汉明重量记为
wt(f)=|1f|。
另设

则x的汉明重量记为
wt(x)=|{xi:xi=1}|。
定义2 设一个n元布尔函数f的Walsh变换
是一个整数值函数,另取

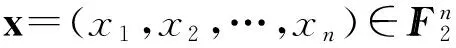
它们的内积
[x·w]2=x1w1⊕x2w2⊕…⊕xnwn,
那么
成为f在点w的Walsh变换系数,f的所有Walsh变换系数的集合称为f的Walsh谱。
定义3 称n元布尔函数f(x)∈Bn为对称布尔函数,如果对任意n×n阶置换矩阵P,恒有
f(x)=f(xP) 。
wt(x)=wt(y),
都有
f(x)=f(y),
则f是对称布尔函数。
根据定义每个n元对称布尔函数f(x)∈Bn可以由一个n+1元向量
来表示,其中分量vf(i)表示重量为i的输入向量的函数值。
度数为i的Krawtchouk多项式的定义为
(i=0,1,…,n)。
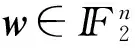
wt(w)=k,
成立下等式
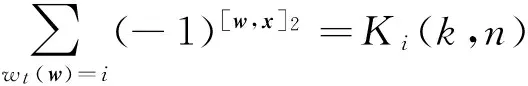
定理1[11]设f(x)∈Bn,Wf(w)表示其Walsh变换,f是n元对称布尔函数当且仅当Wf(w)是一个对称实值函数。
对于n元对称布尔函数f(x)∈Bn,则有
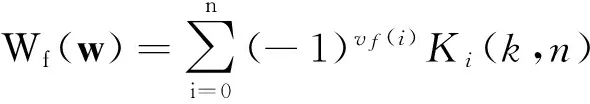
2 算术Walsh变换
关于算术Walsh变换的定义,详细内容可参考文献[4-5]。
定义4 令
={0,1,2,…},
布尔函数f的扩展函数
F:n→ IF2,
F(x1,x2,…,xn)=
f(x1mod2,x2mod2,…,xnmod2)。
扩展集合
Pn={F:F(x+2b)=F(x),b∈n}
是Rn的子集,其中
Rn={F:n→IF2}。
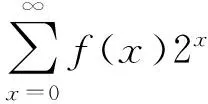
Sn=[(t1,t2,…,tn)]/(t1t2…tn-2)
是同构的,其中
[(t1,t2,…,tn)]=
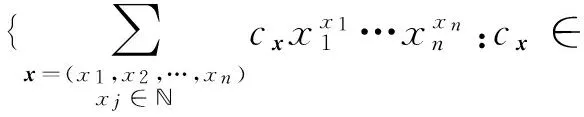
对于任意的x∈n,定义对角线集合
Dx={x+c(1,1,…,1):c∈}。
对于一个固定位于某条对角线上的x∈n,沿着对角线Dx上的所有项的和在同构意义下可定义一个2-adic数
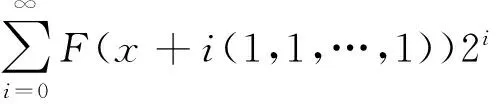
(1)
定义5 对于任意F∈Rn,如果存在一个整数k满足对于任意
x=(x1,x2,…,xn)∈n
(xi≥k,i=1,2,…,n),
使得对于任意b∈n,有
F(x+pb)=F(x),
则F是最终p-周期的。如果对任意
x=(x1,x2,…,xn)∈n,
都有
xi≥k(i=1,2,…,n),
则F在集合
{x+b:b=(b1,b2,…,bn),0≤bi 上的值称为F的一个完整的周期。 假设F∈Rn是严格2-周期的函数,则由式(1)可得 f(x)+f(x+1n)2+f(x)22+…= (2) 定义6 对于任意F∈Rn是最终p-周期的,F的不平衡度为 其中 Un={x=(x1,x2,…,xn): xi∈{0,1},x1=0}。 定义7 一个最终周期的函数F∈Rn的算术Walsh变换定义为实值函数 其中Ta定义为 Ta(b)=[a·b]2(b∈n)。 定理2[12]设f(x)∈Bn是n元对称布尔函数,则f(x)的算术Walsh谱是对称实值函数。 文献[5]利用拉格朗日插值方法求出了布尔函数的算术Walsh谱的计算公式,如下述引理。 引理1[5]令f∈Bn,如果[b·1n]2=0,则 如果[b·1n]2=1,则 [f(x)-f(x+1n)][x·b]2。 利用定理2和引理1可以证明如下定理。 定理3 设f(x)∈Bn是n元对称布尔函数,其向量表示为 如果k为奇数,则有 由定理3和Krawtchouk 多项式的定义我们可以推出如下结论。 推论1 设f(x)∈Bn是n 元对称布尔函数,其向量表示为 如果k为奇数,则有 证明 利用定理3和 (-1)[x·w]2=1-2[x·w]2 即可证明。 推论1给出了对称布尔函数的算术Walsh变换的基于Krawtchouk多项式的一般表达式,根据Krawtchouk多项式的性质,还可得出更加简约的表达式。 定理4[10,15]关于Krawtchouk多项式,成立 K0(k,n)=1, K1(k,n)=n-2k, (i+1)Ki+1(k,n)= (n-2k)Ki(k,n)-(n-i+1)Ki-1(k,n), Ki(k,n)=(-1)kKn-i(k,n), Ki(k,n)=(-1)iKi(n-k,n), 特别当n是偶数且k为奇数时,有 而当n是偶数且i为奇数时,有 定理5 设f(x)∈Bn是n元对称布尔函数,其向量表示为 如果k为奇数,则有 其中 证明 由定理4可知,当k为偶数时,有 Ki(k,n)=Kn-i(k,n), 当k为奇数时, 有 Ki(k,n)=-Kn-i(k,n), 定理得证。 文献[10]给出了一种计算对称布尔函数的经典Walsh谱的快速计算算法,算法的时间复杂度是O(n2),空间复杂度是O(n)。目前尚无文献讨论对称布尔函数的算术Walsh谱的快速实现算法,利用定理5可得出对称布尔函数的算术Walsh谱的快速实现算法。 由于定理5的证明利用Krawtchouk多项式的性质简化了对称布尔函数的算术Walsh谱的Krawtchouk多项式表达式,因此在计算过程中计算出Ki(k,n)后不需要计算Kn-i(k,n),进一步减少了求解过程的运算。该算法的时间复杂度是O(n2),空间复杂度是O(n)。 新算法的主要思想可描述如下。 使用迭代法计算Ki(k,n),不需要存储每个Ki(k,n)。根据定理4可得 (n-i+1)Ki-1(k,n)], K0(k,n)=1, K1(k,n)=2-2k, 在每个循环里计算Ki+1(k,n),只需要暂时存储Ki(k,n)和Ki-1(k,n)的值,在下一轮的计算中会被新的值覆盖。 具体算法可描述如下。 输入 函数变量个数n,对称布尔函数 vf=(vf(0),vf(1),…,vf(n))。 输出 对称布尔函数的算术Walsh谱af。 开始 s=K0(k,n)=1; t=K1(k,n)=n-2k if (k是偶数) h1=vf(0)vf(n); else h1= vf(0)-vf(n); if (n-k是偶数) h2=vf(0)vf(n); else h2=vf(0)-ff(n); if (k是偶数) h1=h1+vf(i)vf(n-i)t; else h1= h1+[vf(i)-vf(n-i)]t; if (n-k是偶数) h2= h2+vf(i)vf(n-i)(-1)it; else h2= h2+(vf(i)-vf(n-i))(-1)it; s=t, t=r; } if (n是偶数){ af(k)=2n-2p+q+2h1; af(n-k)=p-q-h2 } if (n是偶数) { h1=vf(0)vf(n); s=K0(k,n)=1; t=K1(k,n)=n-2k h1= h1+ vf(i)vf(n-i) t; s=t, t=r; } af(k)=2n-2p+q+2h1 } 结束 研究具有特殊密码学性质的对称布尔函数的算术Walsh变换的性质和实现算法。首先证明了对称布尔函数的算术Walsh变换和Krawtchouk 多项式之间的关系,并根据两者之间的关系和Krawtchouk 多项式的性质提出了一种时间复杂度和空间复杂度较低的对称布尔函数的算术Walsh谱的快速计算算法。算术Walsh变换作为对经典Walsh变换的进位模拟,是一种全新的研究布尔函数的方法,其本身的性质有待进一步深入的研究。下一步的工作将重点研究算术Walsh变换和布尔函数的其他密码学性质的联系,以及与算术Walsh变换相关的某种类型的密码攻击。 [1] Carlet C. Boolean Functions for Cryptography and Error Correcting Codes[M]. Cambridge: Cambridge University Press, 2007:4-6. [2] 温巧燕,钮心忻,杨义先. 现代密码学中的布尔函数[M]. 北京: 科学出版社, 2000:1-3. [3] Cusick T, Stanica P. Cryptographic Boolean Functions and Applications[M]. San Diego: Academic Press, 2009:1-10. [4] Klapper A, Goresky M. A With-Carry Walsh Transform (Extended Abstract)[C]//Sequences and Their Applications-SETA 2010, Lecture Notes in Computer Science. Paris: Springer Berlin Heidelberg, 2010: 217-228. [5] Klapper A, Goresky M. Arithmetic Correlations and Walsh Transforms[J]. IEEE Transactions on Information Theory, 2012, 58(1):479-492. [6] Klapper A. Arithmetic Walsh Transform of Quadratic Boolean Functions[C]// Sequences and Their Applications-SETA 2012, Lecture Notes in Computer Science. Waterloo: Springer Berlin Heidelberg, 2012:65-76. [7] Carlet C, Klapper A. On the Arithmetic Walsh Coeffients of Boolean Functions[J/OL].Designs, Codes and Cryptography. (2014-02-30)[2014-05-20].http://cs.engr.uky.edu/~klapper/pdf/AWT-PSF.pdf.DOI:10.1007/s10623-013-9915-3. [8] Canteaut A, Videau M. Symmetric Boolean Functions[J]. IEEE Transactions on Information Theory, 2005, 51(8):2791-2811. [9] Braeken A, Preneel B. On the Algebraic Immunity of Symmetric Boolean Functions[C]//Progress in Cryptology - INDOCRYPT 2005: 6th International Conference on Cryptology in India, Bangalore, India, December 10-12, 2005. Berlin: Springer Berlin Heidelberg, 2005: 35-48. [10] Dalai D K, Maitra S, Sarkar S. Basic Theory in Construct ion of Boolean Functions with Maximum Possible Annihilator Immunity[J]. Design, Codes and Cryptography, 2006, 40(1): 41-58. [11] Dawson E, Wu Chuankun. on the linear structure of symmetric Boolean functions[J]. Australasian Journal of Combinatorics, 1997(16): 239-243. [12] 赵庆兰,郑东.布尔函数性质Walsh谱与算术Walsh谱[J].科学技术与工程,2013,13(17), 4804-4811. [13] Koblitz N. p-Adic Numbers, p-Adic Analysis, and Zeta Functions[M]. New York: Springer, 1984:1-5. [14] Klapper A, Goresky M. Feedback Shift Registers, Combiners with Memory, and 2-Adic Span[J]. Journal of Cryptology, 1997, 10(2): 111-147. [15] Krasikov I. On integral zeros of Krawtchouk polynomials[J]. Journal of Combinatinal Theory: Series A, 1996,74(1):71-99. [责任编辑:王辉] A fast algorithm for computing arithmetic Walsh spectra of symmetric Boolean functions ZHAO Qinglan1, ZHENG Dong1,2 (1.School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2.National Engineering Laboratory for Wireless Security, Xi’an University of Posts and Telecommunications, Xi’an 710121, China) In order to improve the algorithm efficiency for computing the arithmetic Walsh spectra of symmetric Boolean functions, Krawtchouk polynomial is used to study arithmetic Walsh transform of symmetric Boolean functions. Firstly the relationship of Krawtchouk polynomial and arithmetic Walsh transform of symmetric Boolean functions is discussed. Secondly it is proved that the arithmetic Walsh spectra of symmetric Boolean functions has simple expression related to Krawtchouk polynomial. Finally a fast algorithm for computing the arithmetic Walsh spectra of symmetric Boolean functions using properties of Krawtchouk polynomial is presented. This algorithm has low time and space complexity. Boolean functions, Walsh transform, 2-adic number, Krawtchouk polynomial 10.13682/j.issn.2095-6533.2014.05.008 2014-07-07 国家自然科学基金资助项目(61272037, 61070249);陕西省自然科学基础研究计划基金重点资助项目(2013JZ020);西安邮电大学青年基金资助项目(ZL2013-12) 赵庆兰(1981-),女,博士研究生,讲师,从事密码学与信息安全研究。E-mail:qlz@snnu.edu.cn 郑东(1964-),男,博士,教授,从事云计算安全与密码学研究。E-mail: zhengdong@xupt.edu.cn TN918 .1 A 2095-6533(2014)05-0040-06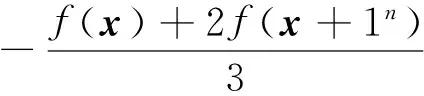
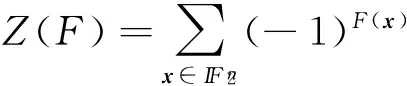
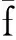
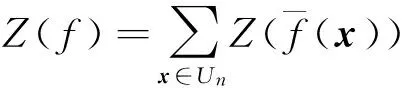
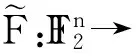
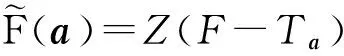
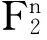
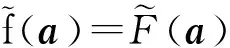
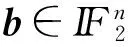
3 对称布尔函数的算术Walsh谱
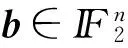
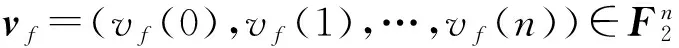
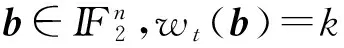
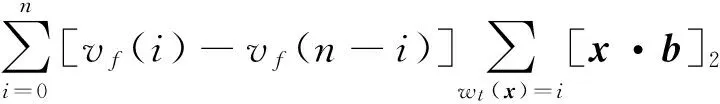
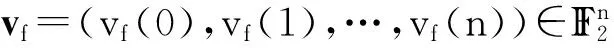
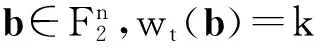
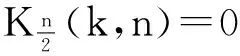
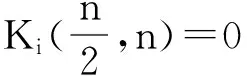
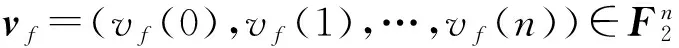
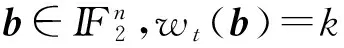
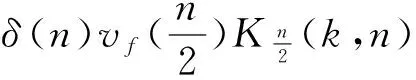
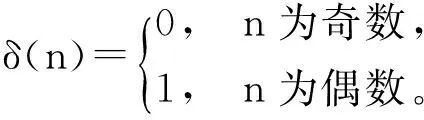
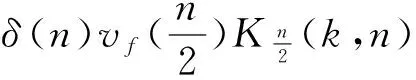
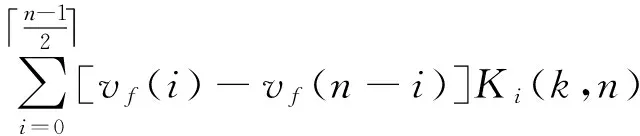
4 算术Walsh谱快速算法
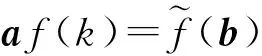
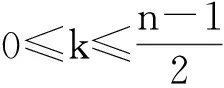
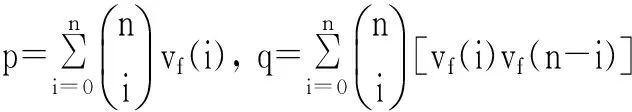
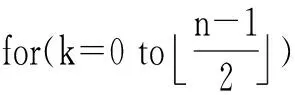
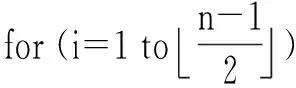
5 结语

