特征值类频谱感知算法的仿真分析
弥 寅, 卢光跃, 关 璐
(西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)
特征值类频谱感知算法的仿真分析
弥 寅, 卢光跃, 关 璐
(西安邮电大学 无线网络安全技术国家工程实验室, 陕西 西安 710121)
为了全面了解基于特征值类的合作频谱感知算法的性能,通过Matlab仿真实验对该类算法进行仿真,以探究门限值随虚警概率的变化、采样次数和认知用户数对检测性能的影响,并分析针对不同信噪比的检测概率和实际的虚警概率。仿真结果显示,基于特征值类的算法不需预知主用户信号和噪声方差信息,能够克服噪声不确定度的影响,相较于传统的能量检测,有着更加稳健的检测性能;基于最小特征值极限分布的改进算法在低信噪比、采样次数和认知用户数较少时,判决门限更低、检测概率更高。
认知无线电;频谱感知;随机矩阵理论;采样协方差矩阵;特征值
随着近些年无线通信技术的显著发展,智能手机、可穿戴设备等增长迅猛,加剧了有限无线频谱资源紧张的局面。在频谱的利用方面,出现了利用率不高、公共频谱拥堵和授权频谱空闲率高等特点。如何改善频谱拥堵现状、有效地提高频谱资源利用率,是下一代无线通信亟待解决的问题[1-3]。美国联邦通信委员会(Federal Communications Commission, FCC)提出的认知无线电(Cognitive Radio, CR)[3]技术可以实现对频谱的二次利用,在不对授权用户(Primary User, PU)造成有害干扰的情况下,使CU能够检测到并合理地利用空闲授权频段,能够有效地缓解频谱拥堵。
频谱感知是实现CR的前提条件和首要任务。CU通过频谱感知,以无监督的方式来发现在特定时间、特定地理位置未被充分利用的“频谱空洞”[4],一方面可以检测到可用的频谱资源,另一方面也限制了对PU造成潜在的干扰,因此CU采用何种的频谱感知方法将直接影响整个CR网络的性能。经典的频谱感知算法[5]有匹配滤波器检测(Matched-Filtering, MF)、能量检测、循环平稳特征检测(Cyclostationary Feature Detection, CFD)等。其中MF算法[6]在加性高斯白噪声环境下性能最优,但其同步要求较高,且必须预知PU发射机信号的先验知识;最常用的ED算法[7]是盲感知,实现简单,但受噪声不确定度影响大,存在信噪比墙(SNR wall)现象,门限设置困难[8];CFD算法[9]利用通信信号本身具有的循环周期特性来检测PU的存在性,性能较好,同为盲感知,缺点是计算较复杂,需要更长的检测时间,降低了系统的灵敏度。
在不同的检测算法中,有不同的门限确定方法。文[1]对现有的算法进行了分类,并对基于特征值和协方差矩阵[10]的感知算法做了详细的综述。通过对Wishart随机矩阵的特征值进行分析,文[11]提出了LSC合作感知算法,采用特征值之比作为检验统计量,门限使用特征值的渐近值直接做近似,检测性能相比ED算法有所提高,但在采样数较小的实际应用情形下性能不够理想。MME算法[12]的检验统计量与LSC算法一致,利用最大特征值的极限分布,结合最小特征值的渐近值,从而推导出给定虚警概率条件下的判决门限,这属于半渐近的理论,在采样数较小的情形下性能优于LSC算法[13]。基于MME算法,文[14]提出了一种改进的NMME算法,利用最大特征值的渐近值,对采样协方差矩阵最小特征值的极限分布进行了研究,从而使判决门限更加精确,算法的检测性能也得到明显提高。文[15]提出了DMM算法,检验统计量采用最大最小特征值之差,在推导判决门限时使用了最大特征值的极限分布,通过估计噪声对门限实时更新,其检测性能明显优于ED算法,并能有效克服噪声不确定度的影响。为了提高实际情形下的感知性能,基于DMM算法,利用最小特征值的极限分布和最大特征值的渐近值,文[16]提出了改进的NDMM算法,在给定虚警概率的条件下,门限判决更加准确,在低信噪比的情况下,检测概率更高,同样属于盲感知算法,并能有效抵抗噪声方差的影响。
本文将针对基于采样协方差矩阵特征值的合作频谱感知算法,通过MATLAB仿真实验,分析门限值与虚警概率之间的关系、采样次数和认知用户数的变化对检测性能的影响、检测概率和实际虚警概率随信噪比的变化,以求得出不同参数对特征值类算法的性能影响。
1 检测模型及理论
基于采样协方差矩阵特征值类频谱感知算法的主要思想是充分利用PU信号与白噪声不同的相关性进行的。通常,频谱感知可以表述为一个二元假设检验问题[17],即存在两种假设:H0表示PU不存在,频段空闲,CU可接入该频段;H1表示PU存在,频段被占用,CU不可接入该频段。因此,频谱感知的数学模型为
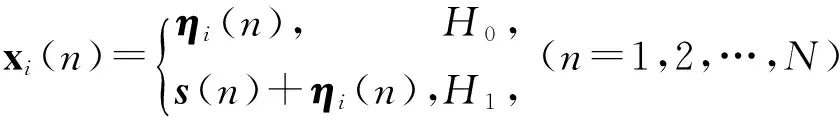
其中xi(n)表示第i个CU在第n个时刻采样到的信号向量;s(n)表示PU发射机信号经过路径损失和多径衰落后被第i个CU接收到的信号向量;ηi(n)表示均值为零、方差为σ2的独立同分布加性高斯白噪声向量。
M个CU对PU发射机信号采样得到的信号构成一个向量
X=[x1,x2,…,xM]T,
同理可得
S=[s,s,…,s]T,
η=[η1,η2,…,ηM]T。
因此,X可以用一个M×N维的矩阵表示为
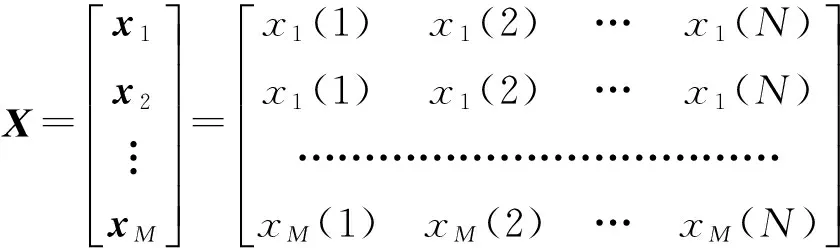
假设S与η相互独立,H1成立时,考虑M个CU接收信号的采样协方差矩阵
RX=E[XXH],
经过信道后的PU信号的统计协方差矩阵
RS=E[SSH],
则有
RX=RS+σ2IM。
实际情况中,由于无法准确计算RX,所以只能用有限的采样来估计协方差矩阵[18],即
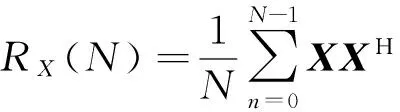
(1)
假设H0成立时,s(n)不存在,即RS=0,则
RX=σ2IM;
而当H1成立时,RS≠0。令RX的最大最小特征值分别为λmax和λmin,RS的最大最小特征值分别为ρmax和ρmin,容易得出
λmax=ρmax+σ2,λmin=ρmin+σ2。
显然,当H0时,有
λmax=λmin=σ2,
而当H1时,有
λmax>σ2=λmin。
也就是说,H0和H1两种情形时,RX特征值分布的差异为频谱感知提供了一条解决思路。通过研究发现,特征值之比与之差能够用来作为检验统计量进行频谱感知判决。
近年来,最新的随机矩阵理论(Random Matrix Theory, RMT)成果不断被应用到频谱感知领域。当H0时,RX(N)为特殊的Wishart随机矩阵[19]。当噪声为实信号时[18],Wishart随机矩阵最大特征值服从1阶Tracy-Widom分布F1(t)。文[20]给出了M-P律,即最大最小特征值的渐近值。有研究表明[21],当M,N→∞时,Wishart随机矩阵最小特征值也服从F1(t)。
利用这些理论可以进行特征值算法的门限确定,渐近理论不够准确,而且在小采样时性能不够理想。半渐近理论结合了特征值的渐近值和极限分布,能够实时地更新门限,提高了准确度,从而改善了算法的检测性能,而且最小特征值的分布比最大特征值的分布函数更加精确。下面对基于特征值之比和之差的算法分别进行介绍。
2 基于特征值类的频谱感知算法
特征值类频谱感知算法可描述如下。
步骤1 进行数据采样,并根据式(1)估计接收信号采样协方差矩阵RX(N)。
步骤2 对RX(N)进行特征值分解,求得λmax和λmin,进而得出检验统计量T,不同的检测方法有不同的T。
步骤3 根据系统设定的虚警概率,利用特征值的渐近值或极限分布,得出判决门限γ。
步骤4 按照规则判决,即当T<γ时,假设H0成立;否则,假设H1成立。
2.1MME算法
MME(Maximum-minimum Eigenvalue)算法[12]的检验统计量为
TMME=λmax/λmin。
在给定虚警概率Pf时,通过分析H0时Wishart随机矩阵最小特征值的渐近值和最大特征值的极限分布,推导出MME算法的判决门限

(2)
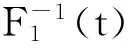
2.2DMM算法
DMM (Difference between the Maximum and the Minimum Eigenvalue)算法[15]的检验统计量为
TDMM=λmax-λmin。
利用最小特征值的渐近值和最大特征值的极限分布,可求得DMM算法的判决门限
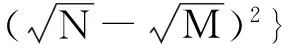
(3)
其中
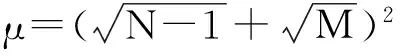
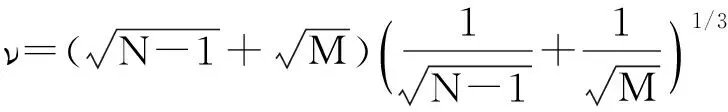
由式(3)的门限表达式可以看出,γDMM与噪声方差有关,为了尽量降低利用最小特征值估计噪声方差时带来的误差,这里对噪声方差进行估计,即
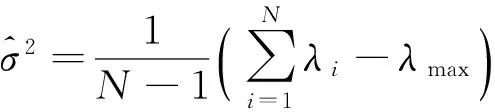
(4)
2.3 NMME算法
随着近些年RMT的发展,文[21]研究发现了最小特征值的极限分布,而且比目前所采用的最大特征值的极限分布函数更精确。因此采用与MME算法相同的检验统计量,在推导判决门限时,使用最大特征值的渐近值和最小特征值的极限分布,由此得出的改进的NMME算法[14]。在噪声为实信号时,虚警概率Pf可表示为
Pf=P{λmax>γNMMEλmin|H0}=
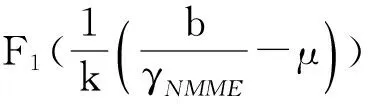
(5)
经变换,求得NMME算法的判决门限
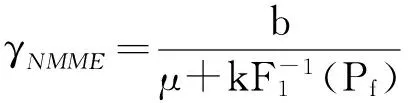
(6)
其中

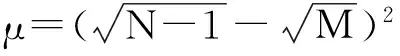

2.4NDMM算法
与NMME算法原理一致,使用最大特征值的渐近值和最小特征值的极限分布推导门限,检验统计量与DMM算法相同,由此得出的改进的NDMM算法[16]。门限表达式为
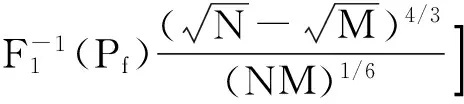
(7)
对于复信号,阈值中的不同仅在于用函数F2代替F1。由式(7)可以看出,NDMM算法的门限也与噪声方差有关。同样需要根据式(4)进行噪声估计,即实现对判决门限的实时更新,从而抵抗噪声方差对算法性能的影响。
3 仿真分析
进行10 000次Monte-Carlo模拟仿真实验。通过考察在给定虚警概率Pf的条件下NMME算法和NDMM算法所能达到的检测概率Pd来评价其性能,并且与原算法、ED算法进行比较。考虑固定路径衰落的情况,PU发送信号为经过升余弦脉冲成型的QPSK调制信号;考虑噪声不确定度的影响,基于特征值类的算法噪声不确定度为1 dB,“ED-xdB”表示有噪声不确定度为xdB的ED算法,估计的噪声方差为

设噪声不确定度
B=max{10 log10α}(dB),
其中α服从[-B,B]的均匀分布。
3.1 门限值曲线比较
选取参数
M=5,N=3 200,RSN=-18 dB,
在不同虚警概率Pf时算法的门限值曲线对比结果如图1所示,从中可知,NMME算法和NDMM算法的门限值曲线缓慢上升,而MME算法和DMM算法的门限值随虚警概率Pf的增加呈递减趋势。
在对相同数据进行感知时,当Pf<0.5时,由于NMME算法和NDMM算法的门限值更小,因此其检测性能将优于原算法;当Pf=0.5时,曲线都相交,即有着相同的门限值,因此二者检测性能相同;当Pf>0.5时,MME算法和DMM算法有着更好的检测性能。由于实际系统的虚警概率Pf都取较小的值,所以NMME算法和NDMM算法的检测性能更加优越。
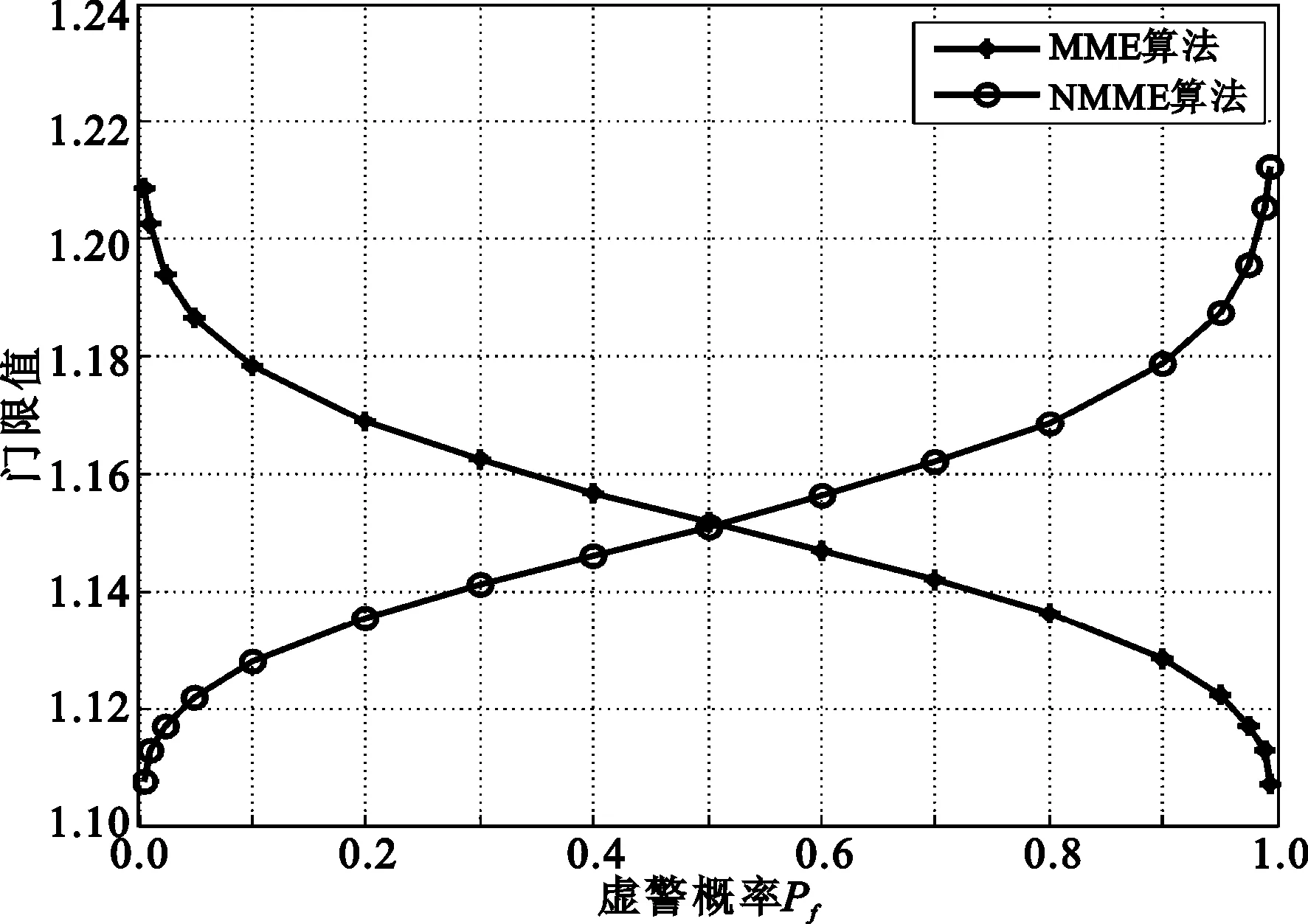
(a) MME算法和NMME算法
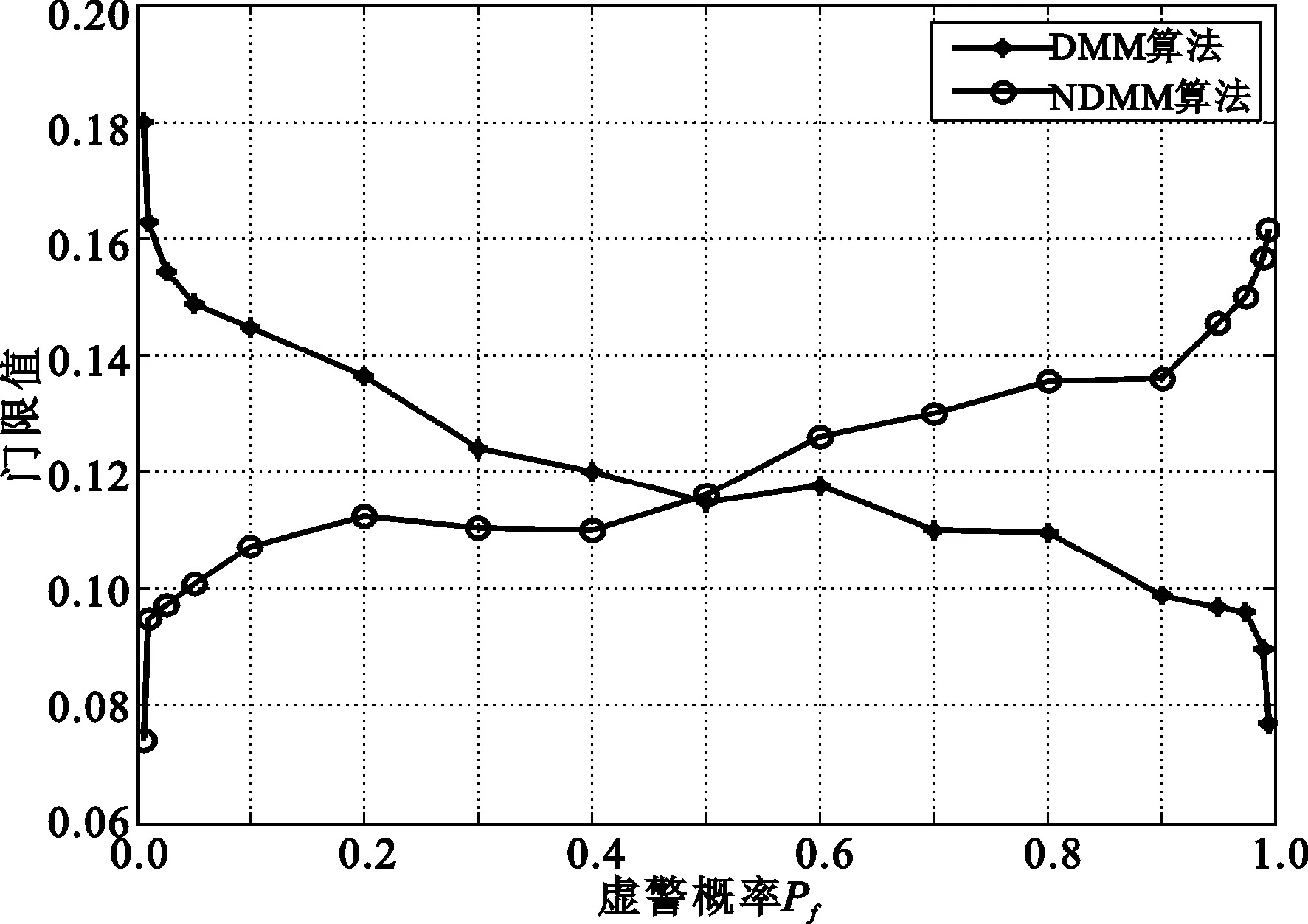
(b) DMM算法和NDMM算法
3.2 检测性能比较
选取参数
Pf=0.1, RSN=-18dB,
采样次数N对检测性能的影响如图2所示,从中可知,如果噪声方差确知(B=0),则ED算法最优。M不变,N增加时,原算法与改进算法的Pd都升高,其中MME算法和DMM算法的性能提升较快。
当N从4 000增大到6 000时,由图2(a),MME算法从22%提高至48%,NMME算法则从91%提高至98%;由图2(b),DMM算法从28%提高至56%,NDMM算法则从90%提高至98%。这与图1分析的结果一致,NMME算法和NDMM算法相比MME算法和DMM算法有着更优越的检测性能。同时发现,ED-0.5dB和ED-1dB算法的性能几乎没有变化,说明通过增加M或N并不能解决噪声不确定度问题。

(a) MME算法、NMME算法和ED算法

(b) DMM算法、NDMM算法和ED算法
认知用户数M对检测性能的影响如图3所示(N=3 200),从中可知,N不变,M增加时,原算法与改进算法的检测性能也得到了提高。
当M从5增加到10时,由图3(a),MME算法从12%提高至89%,NMME算法则从82%提高至100%;由图3(b),DMM算法由16%提高至94%,NDMM算法则从87%提高至100%。同样与图1分析的结果一致。
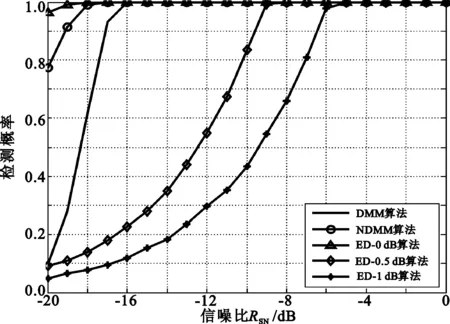
对NMME和NDMM算法的检测性能进行验证。图4是改进算法、原算法和ED算法的检测概率Pd随信噪比变化的曲线(M=5,N=6 400)。
参见图4(a),当RSN=-20dB时,NMME算法的检测概率Pd能达到77%,而MME算法仅达到9%,ED-0.5dB与ED-1dB分别为10%与5%;由图4(b)知,NDMM算法为78%,而DMM算法仅为10%。可以看出,存在噪声不确定度时,ED算法的检测性能明显下降,而改进算法与原算法均不受噪声方差的影响,在低信噪比的情况下,改进算法仍有较高的检测概率,NDMM算法的性能稍好于NMME算法。
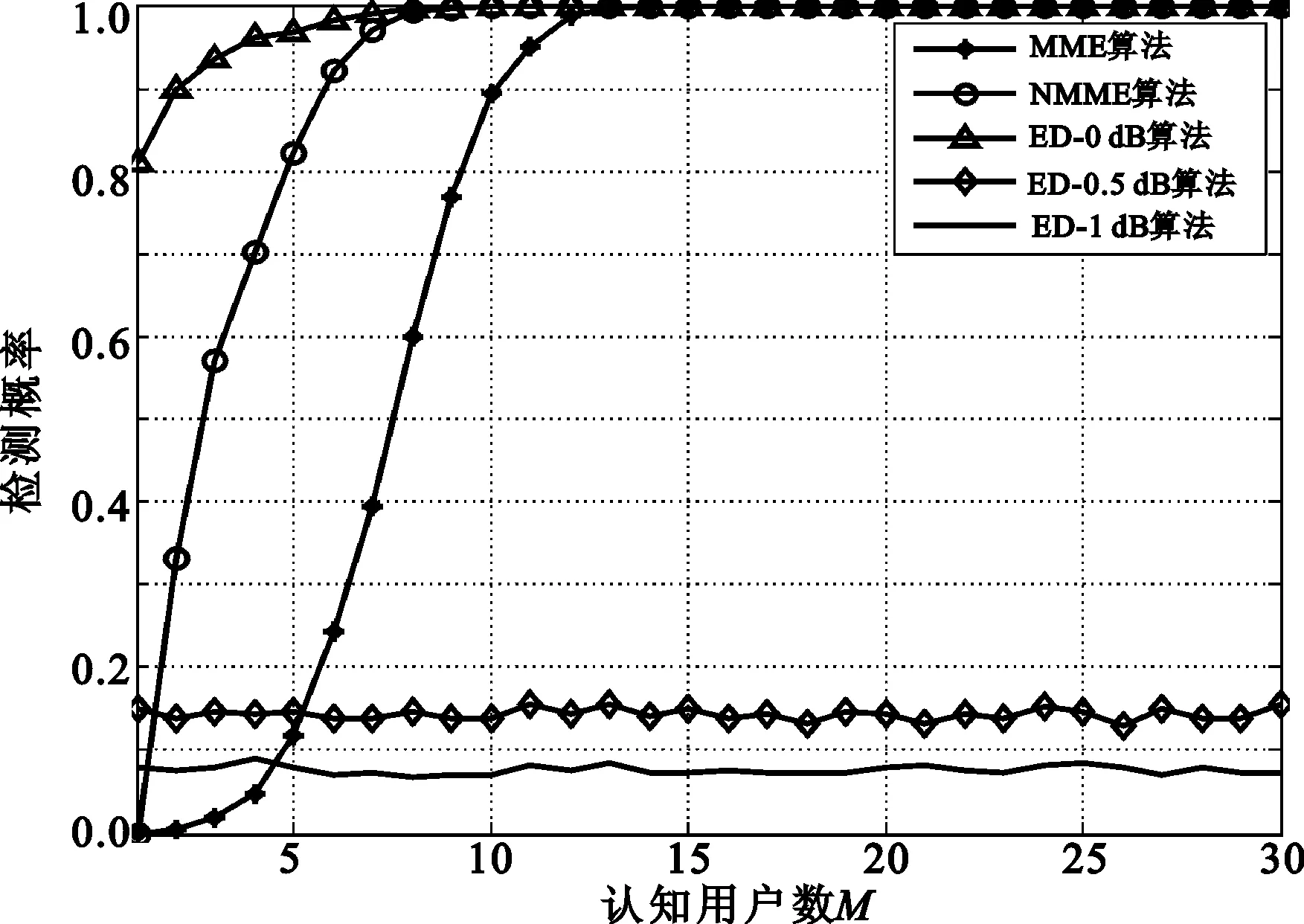
(a) MME算法、NMME算法和ED算法

(b) DMM算法、NDMM算法和ED算法
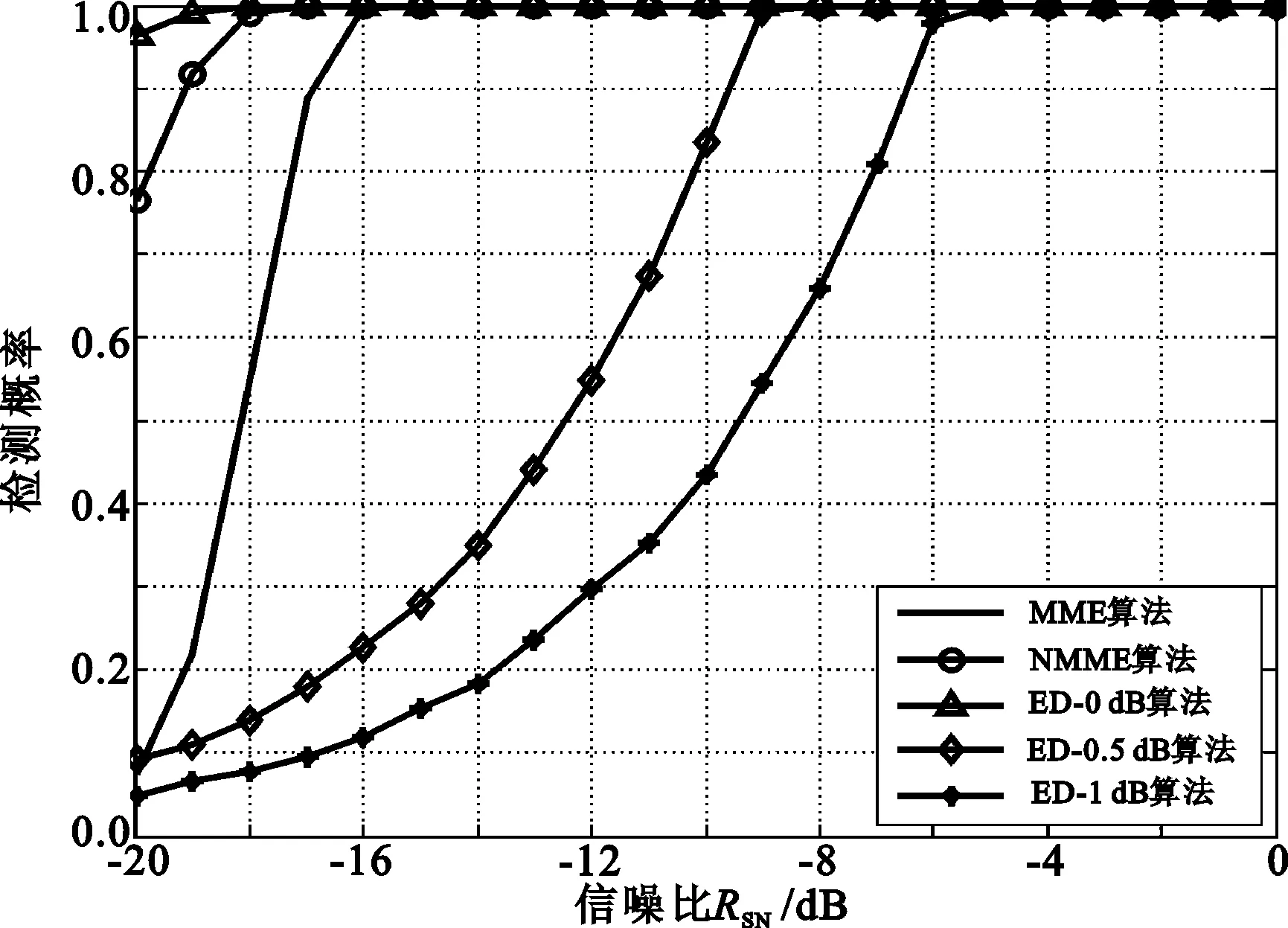
(a) MME算法、NMME算法和ED算法
(b) DMM算法、NDMM算法和ED算法
选取参数
Pf=0.1, N=6 400,
算法的实际虚警概率Pf随信噪比变化的曲线如图5所示,从中可见,改进算法和原算法满足给定虚警概率Pf的要求,而ED-0.5dB与ED-1dB远大于0.1,导致频谱利用率下降,这意味着在噪声不确定度存在的情况下,ED算法很不可靠。
结合图4检测概率Pd随信噪比RSN变化的曲线可以得出,NMME算法和NDMM算法在达到设定虚警概率Pf的同时检测概率Pd最大,充分体现了改进算法的优越性。
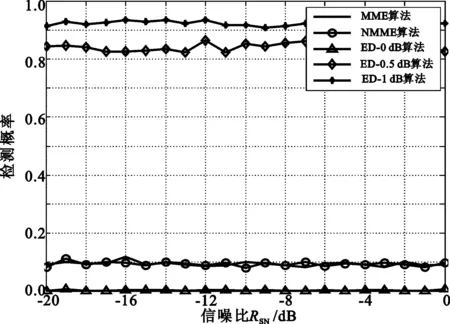
(a) MME算法、NMME算法和ED算法
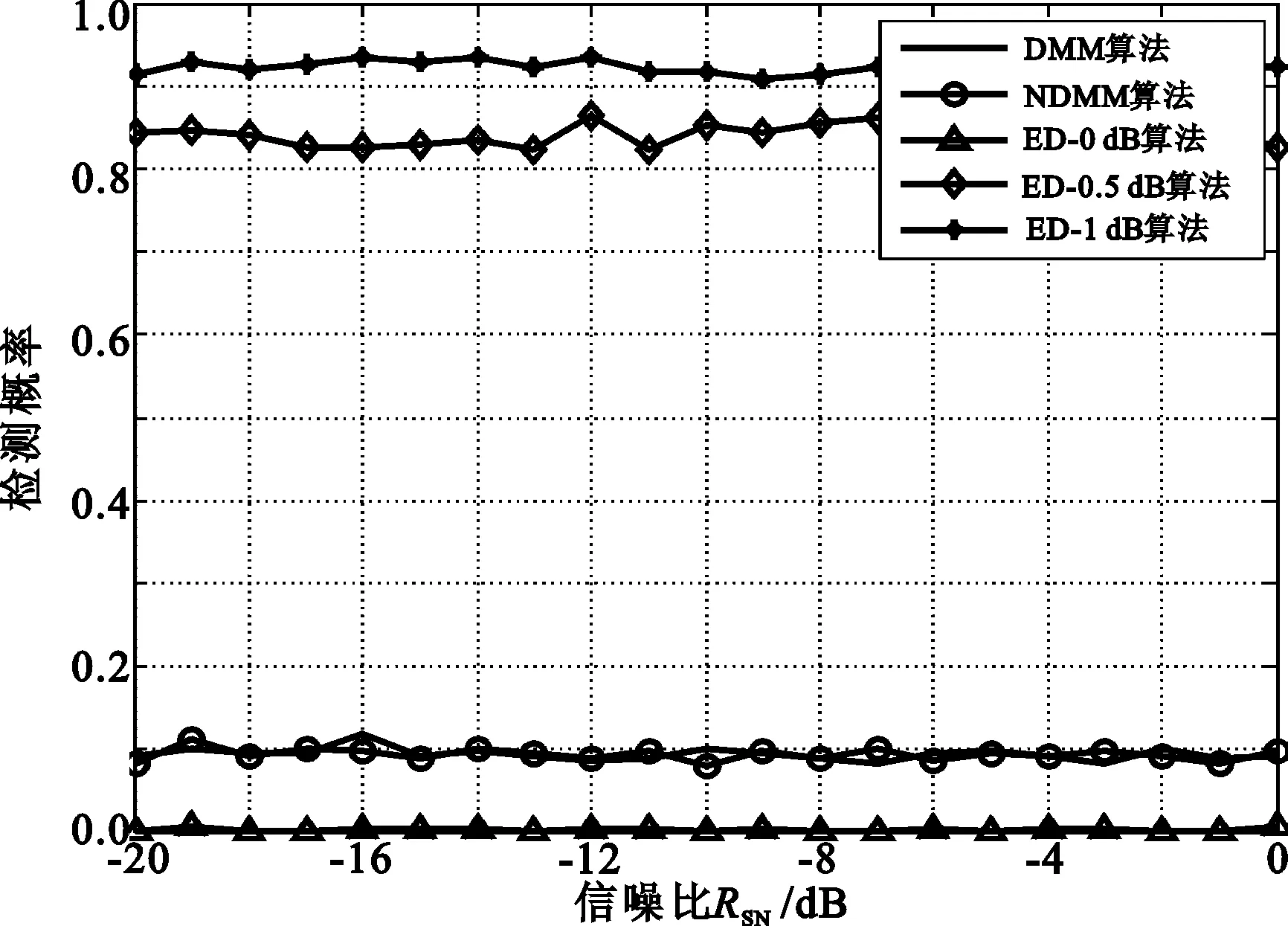
(b) DMM算法、NDMM算法和ED算法
4 结 语
仿真分析了特征值类频谱感知算法。基于MATLAB仿真实验,从门限值和虚警概率的关系、采样次数和认知用户数对检测性能的影响,以及检测概率和实际虚警概率随信噪比的变化等角度,深入分析了特征值类算法的性能。仿真结果表明,相较于传统的ED算法,特征值类算法有更优越的检测性能,实现盲感知并且能够克服噪声不确定度的影响。利用近年来RMT成果,使用最小特征值极限分布提出的改进算法,在虚警概率较小时,判决门限更低,在低信噪比、采样次数和认知用户数较少时,在达到设定虚警概率的同时能获得较高的检测概率,性能更加稳健。
[1] 卢光跃, 弥寅, 包志强, 等.基于特征结构的频谱感知算法[J].西安邮电大学学报,2014,19(2): 1-12.
[2] 宋志群,刘玉涛,王荆宁.认知无线电技术及其应用[M].北京:国防工业出版社,2012:1-10.
[3]FederalCommunicationsCommission.FacilitatingOpportunitiesforFlexible,Efficient,andReliableSpectrumUseEmployingCognitiveRadioTechnologies[J].EtDocket, 2003(03-108):05-57.
[4]HaykinS,ThomsonDJ,ReedJH.SpectrumSensingforCognitiveRadio[J].ProceedingsoftheIEEE, 2009, 97(5):849-877.
[5]YucekT,ArslanH.ASurveyofSpectrumSensingAlgorithmsforCognitiveRadioApplications[J].IEEECommunicationsSurveysandTutorials,2009, 11(1):116-130.
[6]CabricD,MishraSM,BrodersenRW.ImplementationIssuesinSpectrumSensingforCognitiveRadios[C]//ConferenceRecordofthe38thAsilomarConferenceonSignals,System,andComputers.CAMonterey:IEEE,2004:772-776.
[7]DighamFF,AlouiniMS,SimonMK.OntheEnergyDetectionofUnknownSignalsOverFadingChannels[J].IEEETransactionsonCommunications, 2007,55 (1):21-24.
[8]TandraR,SahaiA.SNRWallsforSignalDetection[J].IEEEJournalofSelectedTopicsinSignalProcessing,2008,2(1):4-17.
[9]LundenJ,KoivunenV,HuttunenA,etal.CollaborativeCyclostationarySpectrumSensingforCognitiveRadioSystems[J].IEEETransactionsonSignalProcessing,2009,57(11):4182-4195.
[10] 宋云飞, 卢光跃. 基于采样协方差矩阵的频谱感知算法仿真分析[J]. 西安邮电学院学报,2011,16 (5):12-16.
[11]CardosoLS,DebbahM,BianchiP,etal.CooperativeSpectrumSensingUsingRandomMatrixTheory[C]//3rdInternationalSymposiumonWirelessPervasiveComputing.Luxembourg:IEEE,2008:334-338.
[12]ZengYonghong,LiangYingchang.Maximum-minimumEigenvalueDetectionforCognitiveRadio[C]//The18thAnnualIEEEInternationalSymposiumonPersonal,IndoorandMobileRadioCommunications.Athens:IEEE,2007: 1-5.
[13] 杨晓妮, 卢光跃. 基于特征根比分布的协作频谱感知算法研究[J]. 西安邮电学院学报,2010,15(5): 5-8.
[14] 弥寅, 卢光跃. 一种基于特征值极限分布的合作频谱感知算法[J]. 通信学报,2014:出版中.
[15] 王颖喜, 卢光跃. 基于最大最小特征值之差的频谱感知技术研究[J].电子与信息学报,2010,32(11): 2572-2574.
[16] 卢光跃, 弥寅, 包志强. 特征值极限分布的改进合作频谱感知[J]. 信号处理, 2014,30(3):261-267.
[17]LiuShulei,ShenJ,ZhangR,etal.InformationTheoreticCriterion-basedSpectrumSensingforCognitiveRadio[J].IETCommunications,2008,2(6): 753-762.
[18]BaikJ,benArousG,PecheS.PhaseTransitionoftheLargestEigenvalueforNonnullComplexSampleCovarianceMatrices[J].AnnalsofProbability,2005,33(5):1643-1697.
[19]TulinoAM,VerduS.RandomMatrixTheoryandWirelessCommunications[M].USAHanover:NowPublisherInc, 2004:3-73.
[20]BaiZhidong.MethodologiesinSpectralAnalysisofLargeDimensionalRandomMatrice,areview[J].StatisticaSinica,1999,9(3):611-677.
[21]PennaF,GarelloR,SpiritoMA.CooperativeSpectrumSensingBasedontheLimitingEigenvalueRatioDistributioninWishartMatrices[J].IEEECommunicationsLetters,2009,13(7):507-509.
[22]JohnstoneIM.Onthedistributionofthelargesteigenvalueinprinciplecomponentsanalysis[J].TheAnnalsofstatistics,2001,29(2):295-327.
[责任编辑:瑞金]
Simulation and analysis of eigenvalue-based cooperative spectrum sensing algorithms
MI Yin, LU Guangyue, GUAN Lu
(National Engineering Laboratory for Wireless Security, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
In order to comprehensively analyse the performance of eigenvalue-based cooperative spectrum sensing algorithms, the detailed simulation and analysis of this kind of algorithms are completed by simulation experiments with Matlab based on review. The threshold varies with probability of false alarm, the number of the sampling and the cognitive user (CU) varies with the performance of detection, as well as probability of detection and actual Pf as a function of the signal to noise ratio (SNR) are explored. Simulation results show that the eigenvalue-based algorithms do not need any knowledge of the primary user and noise variance in advance, that they are robust against noise variance uncertainty and that they have better performance than the conventional energy detection. Among them, the improved algorithms based on the limit distribution of the smallest eigenvalue have lower decision threshold and higher Pd than the existing algorithms with low SNR, fewer sampling and CU.
cognitive radio, spectrum sensing, random matrix theory, sample covariance matrix, eigenvalue
10.13682/j.issn.2095-6533.2014.05.006
2014-05-09
国家科技重大专项基金资助项目(2012ZX03001025-004);国家自然科学基金资助项目(61271276, 61301091);陕西省自然科学基金资助项目(2012JQ8011);陕西省国际合作基金资助项目(2013KW01-03);工业和信息化部通信软科学基金资助项目(2014R33)
弥寅(1986-),男,硕士,助教,从事认知无线电研究。E-mail:miyin0404@163.com 卢光跃(1971-),男,博士,教授,主要从事通信信号处理研究。E-mail:tonylugy@163.com
TN92
A
2095-6533(2014)05-0027-07

