一种改进的彩色图像多水印嵌入算法
林椹尠, 李源盛
(1.西安邮电大学 理学院, 陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
一种改进的彩色图像多水印嵌入算法
林椹尠1, 李源盛2
(1.西安邮电大学 理学院, 陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
针对彩色图像的版权认证问题,提出一种改进的多水印嵌入算法,采用量化索引调制(QIM)量化方法与提升小波变换结合,将水印分别嵌入到高频和低频系数矩阵,即将载体图像转换到YCbCr空间后,对三个分量分别进行提升小波变换,再用QIM量化方法在Cb和Cr分量的高频系数,以及Y分量的低频系数嵌入水印。实验结果表明,利用改进算法嵌入的水印具有较好的隐蔽和不可见性。抗攻击性测试结果显示,在高斯噪声、椒盐噪声、JPEG压缩和1/4裁剪四种攻击方式下,改进算法比基于DCT的纹理特征嵌入算法的水印NC平均值分别提升6%、2%、46%、2%,具有更强的鲁棒性。
提升小波变换;多水印嵌入;QIM量化;低频系数;高频系数
数字水印[1-2]主要思想是通过设定好的算法改变数字图像的冗余数据位,将版权信息、公司标志等具有特殊意义的信息嵌入到数字图像中。水印嵌入以后,不影响原数字图像的使用和价值,并且不会被人的视觉系统[3]察觉到,从而起到保护数字图像版权的作用。数字水印一般具有隐蔽性[4]、安全性、鲁棒性和可证明性。
水印算法可分为空域水印算法和频域水印算法。空域水印算法[5]在最不重要的像素位(Least Significant Bits,LSB)嵌入信息,此算法容易实现,但是最低有效位容易被破坏或者丢失,在抗攻击性上难以满足要求。频域水印算法则是在经过频域变换后的系数中嵌入水印,从而提高安全性。文[6]通过使用二维小波变换分别在R、G、B三个分量高频和低频区域嵌入水印,但是二维小波变换后系数是浮点数,计算量大、效率低,并且在进行压缩时,R、G、B分量能量损失严重,不适宜嵌入水印。文[7]通过对图像分块,选出纹理复杂程度较高的块来嵌入水印,如果嵌入的图像块被剪切,那么水印将随之丢失,并且水印嵌入位置的选择范围和水印嵌入信息量也受到很大的局限。
针对上述这些方法存在的问题,在对这些方法深入分析后提出一种在YCrCb空间域上,基于量化索引调制(Quantization Index Modulation, QIM)量化方法[8]与提升小波变换相结合的高频和低频系数同时嵌入水印的算法,简称IQIM量化算法,目的在于加大水印嵌入量同时提高抗攻击性能。
1 数字水印相关技术
1.1 离散余弦变换
离散余弦变换(简称DCT)具有很好的能量压缩能力和较强的去相关能力[9]。基于纹理特征的DCT水印嵌入的主要思想是将彩色图像某个分量图像分块,选出图像子块中方差最大的n个分块,对各分块进行DCT变换,然后将水印嵌入到n个分块的中频系数上。经过DCT变换后,图像能量主要集中在低频系数上,将水印嵌入低频系数上具有较好的鲁棒性,但嵌入后图像降质较明显,故一般选择在中频区域嵌入水印。
1.2 提升格式小波变换
提升小波变换(Lifting Wavelet Transform, LWT)也称为第二代小波变换。提升小波的基本思想是通过多项式插补获取信号的高频信息,构建尺度函数来获取信号的低频信息。规范的提升方法由 3 个步骤组成:分解(Split)、预测(Predict)和更新(Update)。与传统的第一代小波类似,在对图像的处理中,提升小波变换将图像分为水平(HL)、垂直(LH)和对角线(HH)三个高频子带以及一个低频子带(LL),图像的大部分信息集中在低频子带,高频子带则代表图像的水平、垂直和对角线的边缘信息,而经DCT变换后的图像却无法反映出图像的边缘信息。与传统的第一代小波变换相比,提升格式具有以下优点:(1)继承了第一代小波的多分辨率特征;(2)不依赖于傅立叶变换;(3)效率高,利用复合幅值,减少了浮点运算量,小波变换后的系数是整数,计算速度快;(4)图像的恢复质量与变换时边界采取何种延拓方式无关;(5)计算时无需额外的存储开销,实现了本位操作,不需要辅助寄存器,节省了内存。
1.3 水印置乱处理
水印置乱的目的是用一定的规则打乱图像中像素的位置或颜色,使图像变得杂乱无章,人眼无法辨认出原图像,在图像恢复的过程中,置乱变换将会把原先遭到损坏的比特分散到全图中,这样就减少损坏部分对人视觉的影响。在水印的预处理阶段,可以通过置乱去除水印图像像素间的相关性,分散错误比特的分布,从而提高数字水印的鲁棒性。
为了保证水印的安全性,考虑到置乱时间和复原时间开销选择,对将要嵌入的水印进行N次Arnold变换[10],破坏其空域的相关性,以抵抗压缩旋转等攻击。对于一副大小为N×N的图像,Arnold变换式为

(1)
其中x,y∈{0,1,…,N-1}。Arnold变换经过之乱后图像变得杂乱无章,但Arnold变换具有周期性,重复经过一定次数的变换后可以还原出原始图像,Arnold变换周期如表1所示。

表1 常用图像尺度Arnold变换周期表
给出Arnold置乱的实例,结果如图1所示。


2 改进的QIM量化多水印嵌入算法
2.1 QIM量化嵌入算法
QIM量化方法是一种非线性方法,根据嵌入的二值水印信息0,1的不同,选择相应的量化方法,具体过程分为以下3步。
第1步:对原始图像进行提升小波变换,得到变换后的系数矩阵,用Sk(i,j)(k=LH,HL,HH)表示变换后的高频细节系数,分别代表水平、垂直和对角线高频细节系数。
第2步:由密钥确定嵌入水印的位置(i,j),对同一级的三个小波细节系数进行排序,使得
Sk1(i,j) k1、k2、k3∈ {LH,HL,HH}, 对Sk1(i,j)和Sk3(i,j)间的值进行量化分段,即 (2) 其中Q是常量,Q越大量化层次就越多,嵌入后的图像在视觉上降质的可能性就越小,但提取出的水印可能就越不准确。Q的取值需要使用者作折衷选择。这里Q值取3。 第3步:量化分段后,当嵌入的水印信息为0时,Sk2(i,j)向最靠近它的实垂线量化,当嵌入的水印信息为1时,Sk2(i,j)向最靠近它的虚线量化,如图2所示。 Sk1(i,j) Sk3(i,j) 图2 量化分段示意图 2.2QIM量化算法的实现 嵌入水印信息的基本步骤如下。 步骤1 选择1张1024×1024的彩色图像作为原始载体图像,3张64×64的二值图像作为水印图像,并对水印图像进行Arnold置乱变换预处理。 步骤2 将图像从R、G、B空间转换到YCrCb空间,然后将Y、Cr、Cb3分量分离。 步骤3 在Cr、Cb分量的上,经过二维提升小波变换后得到4个系数矩阵,其中有3个高频子带RcHint、RcVint、RcDint和一个低频子带RcAint,其中,RcHint、RcVint、RcDint分别代表水平、垂直和对角线的3个高频系数。 步骤4 运用QIM量化算法,通过改变3个高频系数中排序在中间位置的高频系数,完成对高频区域水印的嵌入。 2.3 改进的QIM量化算法的实现 QIM量化嵌入算法实现了将水印嵌入到提升小波变换后的高频系数,虽然嵌入水印后有良好的不可见性,但却无法抵抗低通滤波攻击。为了保证水印的抗低通滤波特性,对QIM量化算法加以改进,得出IQIM量化算法。 分别对Cr和Cb分量的高频系数嵌入水印后,在Y分量的低频系数YcAint嵌入水印来提高安全性[11-12]。在Y分量低频系数选择相应的嵌入位置,运用嵌入公式 (3) 改变嵌入位置系数来完成水印嵌入。 上式中YcAint(i,j)为Y分量高频系数矩阵点,w(i,j)为经过处理后的0,1水印矩阵的像素点,λ、γ为拉伸因子。由于此算法是将水印嵌入到低频系数上,而图像的能量大部分集中在低频系数上,因此,拉伸因子过大会影响图像质量,另外随着拉伸因子的变化嵌入水印的可见性也会有所不同。经过多次实验,折衷选取 λ=0.008,γ=0.006。 IQIM量化算法嵌入水印的过程如下。 步骤1 将图像转换到YCbCr空间上,对每个分量进行提升小波变换得到3个高频系数RcHint、RcVint、RcDint和一个低频系数RcAint。 步骤2 按照原QIM量化方法的步骤4改变Cb、Cr分量的高频系数来实现高频水印的嵌入。 步骤3 运用公式(3)改变Y分量的低频矩阵系数完成对低频系数的水印嵌入。 步骤4 将3个分量嵌入水印后的4个矩阵系数进行提升小波逆变换,再进行图像融合,可得到嵌入水印的图像。 2.4 IQIM算法的水印提取 提取过程与嵌入过程相反。 步骤1 将嵌入水印的图像进行空间转换,对图像进行Y、Cb、Cr3分量分解。 步骤2 对Cb、Cr分量高频系数的水印,按照原QIM量化方法的步骤3和步骤4的逆方法提取。 步骤3 对Y分量低频系数的水印,用公式(3)的逆向公式提取出低频的水印。 步骤4 对提取出的3个水印进行Arnold逆变换得到水印图像。 3.1 水印的嵌入结果 基于MATLAB7.0平台,选取1024×1024的彩色图像作为水印嵌入的原始图像,嵌入三个分量的水印图像为64×64的二值图像,结果如图3所示。 (a) Cb分量高频水印 (b) Cr分量高频水印 (c) Y分量低频水印 (d) 待嵌入水印载体图像 (e) 嵌入水印后的图像 用峰值信噪比(Peak Signal to Noise Ratio, PSNR) (4) 来衡量嵌入水印的效果。上式中 而p′(i,j)和p(i,j)分别是嵌入水印后和嵌入水印前的像素点,M和N代表行和列。 PSNR值RPSN可以评价水印算法的隐蔽性,RPSN值越大,水印的不可见性越好,通常情况下,当RPSN>30 dB时,人眼就无法察觉到原始图像和含水印图像之间存在的差异。 使用公式(4)可得IQIM算法的PSNR值为57.99 dB,可见,IQIM算法嵌入水印后的图像基本与原图像无视觉差别,其峰值性噪比明显高于文[7]的41.57 dB,嵌入效果相对要好。 3.2 水印的提取结果 水印提取结果如图4所示。 (a) Cb分量提取水印 (b) Cr分量提取水印 (c) Y分量提取水印 图4 水印提取结果 采用归一化相似系数来衡量提取出的水印和原始水印的相似程度。归一化系数定义为 CN(W,W′)= (5) 其中W和W′代表原始水印和提取出来的水印。对未受任何攻击的图像,Cb分量水印的归一化相似系数为0.999 8,Cr分量水印的归一化相似系数为1.000 0,Y分量水印的归一化相似系数为1.000 0。归一化相似系数越接近1,则提取出的水印越接近于原始水印,因此,IQIM算法可以将水印从图像中完好的提取出来。 3.3 水印的抗攻击性分析 对嵌入水印的图像分别加入高斯噪声和椒盐噪声,以提取水印与原始水印的相似程度来检查水印的抗攻击性,并计算出归一化相关系数作为算法鲁棒性的评价标准。 给嵌入水印图像加入均值为0,方差为0.002高斯噪声,提取水印结果如图5所示。给图像加入均值为0,方差为0.005的椒盐噪声,提取结果如图6所示。对图像进行JPEG有损压缩,压缩因子为80,提取结果如图7所示。剪切1/4水印图像,提取结果如图8所示。 (a) 加入噪声图像 (a) 加入噪声图像 (a) JPEG压缩图像 (a) 1/4剪切后图像 根据实验结果和表3可以看出,对图像进行常见的攻击后,提取出水印的图像质量虽然有所下降,但仍能将三个分量的水印完整的提取出来,可见,该水印算法具有良好的稳健性。对文献[7]算法进行相同的攻击后,三个分量提取出水印的归一化相似系数如表4所示。 表3 IQIM算法提取水印归一化相似系数值 表4 文献[7]算法提取水印的归一化相似系数值 对比表3和表4的可以看出,IQIM算法的抗攻击性能总体上明显优于文献[7]中基于DCT的纹理算法,特别是在抗JPEG有损压缩攻击方面[13]表现出更优的性能。 利用提升小波变换和量化算法的特性和优点,提出了高、低频多水印嵌入的算法,为了在低频嵌入水印,既保证水印的鲁棒性,又使嵌入水印不致影响寄主图像的质量,故可选择数值较小的两个拉伸因子λ和γ。在高频嵌入水印可增加嵌入水印的信息量,又可以保证嵌入水印的不可见性。仿真实验结果表明新算法嵌入水印具有不可见性,在无攻击情况下,从视觉上很难看出提取出水印后和原始图像的差别。在对抗噪声、压缩等常见的攻击具有优越的抗攻击性能,攻击后提取出水印的归一化相似系数均在0.8以上,可以实现版权保护和恶意篡改认证的功能。新算法对现有的图像压缩标准(如 JPEG、 MPEG)具有较好的稳健性,但对更高压缩算法则不能保证也具有同样好的鲁棒性,这也将是下一步继续深入研究的方向。 [1] Cox I J, Kilian J, Leighton T. Secure spread spectrum watermarking for multimedia[J]. IEEE Transactions on Image Processing, 1997, 6(12): 1673-1687. [2] Hsu C T, Wu J L. Hidden digital watermarking in images[J]. IEEE Transactions on Image Processing, 1999, 8(1):58-69. [3] 刘思奇,吕建平.视觉系统结合小波域的水印算法[J].西安邮电学院学报,2012,17(2):89-93. [4] 杨钒,薛模根,崔松.一种兼具版权保护及窜改认证双重功能的数字水印算法[J].计算机应用研究,2009,26(8):3050-3052. [5] 蔺鹏.基于小波变换的彩色图像数字水印技术的研究[D].兰州:兰州理工大学,2005:19-21. [6] 王侃.彩色图像双水印嵌入算法研究[D].北京:北京交通大学,2012:15-41. [7] 柏均,郑泽国.基于RGB空间的DCT域彩色图像水印算法[J].现代电子技术,2010, 4(26):26-28. [8] 黄羿博.基于QIM的自适应音频水印算法研究[D].兰州:兰州理工大学,2011:20-24. [9] 严亚俊,梁猛,陆蓉.一种基于离散余弦变换的数字水印算法[J].西安邮电大学学报,2013,18(5):42-44. [10] 秦海,孙刘杰.基于Arnold置乱自适应图像数字水印法[J].微计算机信息,2010, 26(2):208-210. [11] 吕海翠,傅鹂,王丹.小波变换的低频数字水印[J].计算机工程与应用,2009,45(11):99-101. [12] 贺兴华.Matlab7.x图像处理[M].北京:人民邮电出版社,2006:13-68. [13] 王立平,喻东芝,刘思奇.基于DWT和DCT相结合的数字图像水印算法[J].西安邮电学院学报,2010,15(3):113-115. [责任编辑:王辉] An improved multiple watermarking algorithm for color image LIN Zhenxian1, LI Yuansheng2 (1.School of Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2.School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China) An improved multiple watermark embedding algorithm is put forward in this paper for the problem of color image copyright authentication. Combined with QIM quantitative and lifting wavelet transform, the watermark are embedded into high frequency and low frequency coefficient matrix. The carrier image is transformed into YCbCr space, the three component into the lifting wavelet transform. Then the QIM quantization method is used in high frequency coefficients of Cb and Cr component, and Y component of low frequency coefficients to embed watermark. Experimental results show that embedded watermark obtained by the improved algorithm has good invisibility and concealment. Anti attack test results show that, compared with the texture feature embedding algorithm based on DCT, the watermark NC average values obtained by the improved algorithm of are increased by 6%, 2%, 46%, 2% under the four attacks of the Gauss noise, salt and pepper noise, JPEG compression and 1/4 clipping respectively. Therefore the improved algorithm is more robust. lifting wavelet transform, multiple watermark embedding, QIM quantization, low frequency coefficient, high frequency coefficient 10.13682/j.issn.2095-6533.2014.06.010 2014-06-30 林椹尠(1969-),女,博士,教授,从事小波理论及其应用研究。E-mail:lzhx126@126.com 李源盛(1988-),男,硕士研究生,研究方向为信号与信息处理。E-mail:756473017@qq.com TP309 A 2095-6533(2014)06-0053-05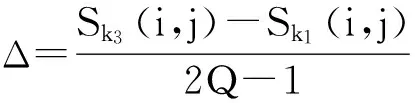

3 实验结果与性能分析





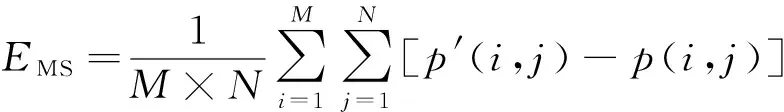



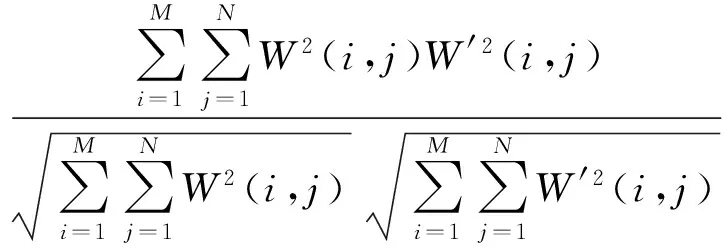






4 结论

