发动机零件泄漏测试传热分析

王勐喆，张 钧，王恩禄，汪丽芬

(1.上海交通大学 机械与动力工程学院，上海 200240；2.上海通用汽车有限公司，上海 201206)

发动机零件泄漏测试传热分析

王勐喆1，张 钧2，王恩禄1，汪丽芬1

(1.上海交通大学 机械与动力工程学院，上海 200240；2.上海通用汽车有限公司，上海 201206)

针对车用发动机零部件泄漏测试过程中温度差异导致结果偏差的问题，对泄漏测试中各过程建立数学模型，并采用集总热容法对测试过程进行瞬态分析和数值模拟。研究结果表明在发动机零部件泄露测试过程中，其第一阶段即充气和稳压阶段零件被测容积能够达到压力和温度平衡，即充气参数和充气过程并非测试结果偏差的因素；在其第二阶段即测试阶段，零件温度会依负指数规律随时间变化，是导致测试结果偏差的主要原因。进一步给出了气体温度变化关系式，为发动机零部件泄漏测试提供参考。

发动机装配线；泄漏测试；温度补偿；数值模拟；集总参数法

0 引言

车用发动机结构中存在包括冷却水回路、润滑油路、气缸等多个密闭腔体。在发动机工作过程中这些腔体需要保持高度的密封性，因此在发动机生产过程中，各零件的密封性测试是零件合格与否的重要标准。现代发动机生产过程中，干式检测法普遍地应用于生产线自动化测试[1]。干式检测法的应用方式主要是在被测容积内外制造压力差，并通过检测压力变化、或与标准件相连检测由压差产生的流量，从而得到零件的泄漏率[2]。

泄漏并非是引起零件内部压力变化的唯一因素，零件内气体的温度同样是内部压力的影响因素之一。实际生产中，由于季节、天气的不同，生产环境温度也会有所不同；根据生产工序的不同，进入测试环节的零件温度与环境温度也就有所不同。测试环节采用的充气源温度也可能对测试结果产生影响。由于对各种温度条件的控制成本较高、加之会拖慢生产节拍[3-4]，因此相比于在测试前对零件、设备等进行强制冷却，在测试环节中通过温度补偿抵消温度的影响是目前较为普遍的处理方式。

生产实践中应用温度补偿的方式，通常是对特定型号零件进行多次基准测试，从而得到测点温度与泄漏率的经验曲线，实际生产时根据这一经验曲线进行补偿处理。由于不同型号零件的测试结果无法通用，该方法在实际使用中存在精度有限、应用成本较高等问题[3]。现有研究也基本围绕实验结果进行经验分析，多数采用直线对数据进行拟合[2-4]，并发现在温差较大时试验数据可能不符合线性规律[2,9]。

为提供温度补偿的理论依据、减少温度补偿方案的设计成本，对干式检测法的各环节分别进行分析。干式检测法一般具有四个典型环节：充气、稳压、检测和放气[5]。其中前三个环节的温度特征均有可能对检测结果产生影响。根据各环节的特点，将整个测试流程分为两个阶段，分别各阶段的特征、建立数学模型并通过数值模拟进行验证，得出被测气体温度的变化规律。所得研究结果可以简化温度补偿的实验流程，为适应性更强的温度补偿方案提供理论依据。

1 测试过程分析

本研究以某汽车公司生产的某型号发动机缸盖为研究对象，其测试参数如下：

位置测试方法充气时间(s)稳压时间(s)测试时间(s)测试压力(bar)泄漏限值(cm3/min)油道压差法4.51141.7512水道流量法10.561.75-1.936

由于零件在进入泄漏测试之前，可能经过加工、清洗等操作，在测试开始时零件温度往往高于环境温度5 K左右。因此选取环境温度293 K，零件初始温度303 K的典型情况进行研究。

1.1 充气和稳压阶段

对常见的测试流程而言，充气和稳压是对同一过程的初态和末态的人为区分，稳压阶段中被测容积仍与恒压气源接通，各已知量没有任何改变，因此可以作为一个完整的过程进行分析。

对某型号发动机缸盖的水道和油道的充气和稳压阶段测试，得到压力曲线如图1、图2所示。

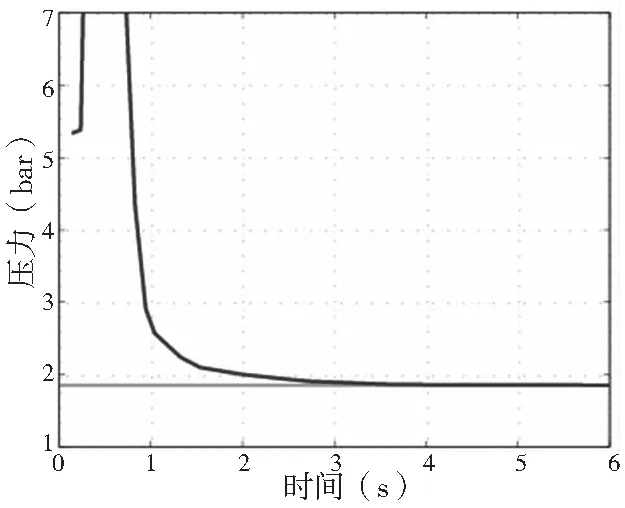
图1 缸盖水道测试过程压力变化

图2 缸盖油道测试过程压力变化

从图 1、图 2可知，水道和油道压力均在5s以内达到平衡，小于充气和稳压阶段的总时间(10～15s)。在压力能够达到平衡的前提下，可对该阶段建立数学模型。

1.1.1 充气和稳压阶段数学模型

在不高于2bar，接近室温的环境条件下，空气可近似为理想气体。假设充气口不发生热传导，忽略重力势能，对充气直到压力平衡的过程进行建模。

由能量平衡可得控制体内能量变化：

ΔUCV=uFmF-uImI=hin(mF-mI)+Q1

其中

Q1=ΔQ-∫houtdmout

(1)

平衡时容积压力与充气压力相同：

ρFTF=ρinTin

式中：

ρin,Tin,hin——恒压气源的气体密度(kg/m3)、温度(K)、比焓(J/kg)；

uI,mI,TI——充气前容积内气体的比热力学能(J/kg)、质量(kg)、温度(K)；

uF,mF,TF——达到平衡容积内气体的比热力学能(J/kg)、质量(kg)、温度(K)；

hout,mout——泄漏气体的比焓(J/kg)和质量(kg)，在整个测试过程中为变化量；

ΔQ——测试过程中气体从容器壁吸热量(J)。

整理以上等式，得到压力平衡时容器内温度：

(2)

式中:除Q2外其余均为已知量。其中Q2为容积内气体与容器壁的热交换以及泄漏导致的能量损失的总和(J)。

根据换热量Q1的范围，即可给出压力平衡时气体温度的上下界。首先考察Q1=0的绝热条件。

对于本文的研究对象，其水道体积为V=0.82×10-3m3。恒压气源温度可视为环境温度Tin=293K，容积内气体初始温度近似为零件进入检测设备时的温度Tin=303K。充气和稳压阶段共历时15.5s。假设充气过程绝热、无泄漏，则有Q2=0。计算得到：

TF=341.1K

充气达到平衡后的温度明显高于初始温度和充气温度。这是由于高压气体所携带的推动功转化为容积内热力学能所致。由于实际情况中不可能达到绝热，该温度也是实际测试中终态温度的上界。

再考察Q1≠0的情况，由于绝热无泄漏条件下平衡态温度高于壁温和环境温度，因此在有自发能量交换的条件下，平衡温度只可能低于前述温度。根据式(2)可知Q1<0。因此温度下界应为气体向容器壁放热最多，即气体与容器壁充分热交换，达到容器初始温度。

1.1.2 热平衡模拟

由于气体与零件壁的传热量与零件形状密切相关，因此基于1.1.1确定的温度上下界，采用数值模拟确定测试过程中的导热特征。

由发动机CAD模型提取冷却水道的腔体模型，并将零件体简化为壁厚不小于1mm的长方体。采用平均边长为2mm的四面体单元划分网格，并在大曲率位置加密。

使用Fluent针对压力达到平衡后的情况进行瞬态模拟，初始条件为流体域压力1.75 bar，温度293 K，固体域温度303 K。由于被测容积与气源压力平衡，流动仅有自然对流，在10 K的温差和约65 mm的尺度下，可根据竖直平板自然对流关系求得瑞利数Ra：

APN TOC模式是国外的TOC的主要模式之一。国际护理协会将APN定义为一名注册护士，其拥有深厚的专科知识、复杂问题的决策能力及扩展临床实践的才能[9]。2002年，Brooten等[10]建立APN TOC模式并将其应用于患者的综合出院计划。与其他TOC模式不同的是，APN是Naylor建立TOC模式的核心，其先进的护理实践技术和丰富的成功经验，可帮助患者在环境变化过程中顺利完成过渡。虽然由不同身份的医疗卫生保健人员领导的TOC模型多种多样，但Naylor[7]研究表明，由APN领导的团队管理项目中最有效地降低再住院率，证明TOC模式可预见性地将照顾者与APN联系，以确保患者平稳过渡。

由于瑞利数远低于层流向湍流过渡的临界值109[6]，因此可认为模拟中仅发生层流流动。依据以上前提采用基于压力的Coupled求解算法，在压力、密度和能量分量上采用二阶迎风格式以获得较高的精度。采用0.1s的时间步长进行非稳态计算，计算结果如图 3所示。

图3 温度平衡模拟(T0=293 K, p=1.75 bar)

图中三条实线自上而下分别为流体域内的最高温度、平均温度和最低温度，虚线为平均温度与终态温度的差值。由图可见流体域温度变化与时间呈对数关系，根据模拟结果，最低温度与零件壁温度的差值在3.3s后即减至0.5 K以下。

采用同样的参数，模拟腔内气体由341 K降温的过程，所得计算结果如图 4所示。

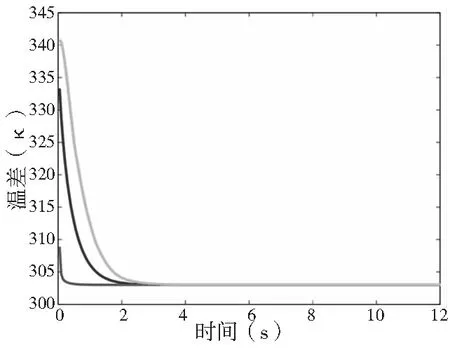
图4 温度平衡模拟(T0=341 K, p=1.75 bar)

对传热过程的模拟同时得出了自然对流下零件内表面的传热系数：

h=111.78W/m2·K

(3)

由图 4可知，流体域温度以对数时间规律趋近于零件壁温，结合1.1.1得出的温度范围，可知在充气和稳压过程结束时，被测容积能够达到温度平衡。

1.2 应用集总热容法分析零件整体散热

1.2.1 前提条件

因此可对零件整体采用集总热容法进行瞬态分析，忽略零件与零件内容积的热交换，仅考虑外部空间与零件体的热交换。首先验证应用集总热容法的前提条件，假设测试阶段零件外部无强制对流，计算Bi数：

其中当量长度L采用零件体积和暴露在外部的表面积之比；根据零件外部与内部在形状、尺度、环境上的相似性，对流换热系数采用式(3)中的值进行计算。

由于计算出的Bi数远小于应用集总热容法的上限值[7]，可见对于20倍以内的对流换热系数变化，均适用于集总热容法分析。

1.2.2 瞬态分析

由集总热容法温度与时间的关系式：

其中，无量纲时间Fo为：

可得到零件温度随时间变化的关系：

(4)

由上式可得到零件温度随时间变化的曲线。

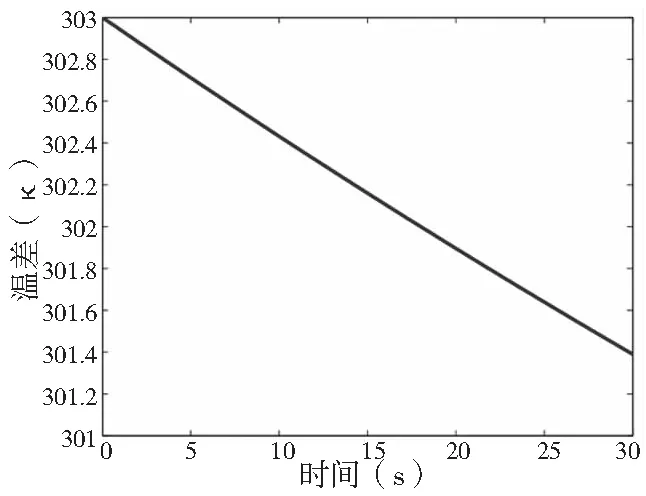
图5 零件温度随时间变化的关系

由式(4)和图5可以看出，温差与时间的关系为负指数关系，但时间与温度跨度较小的局部曲线近似于线性规律。

进一步研究零件腔体内空气的温度变化规律，由于已知零件内壁与腔体内气体的对流换热系数，由对流换热关系式和能量守恒列出方程组：

与式(4)联立得到一阶微分方程组，可求得被测容积内气体温度随时间变化的关系式。代入上文条件，求得的气体温度与零件温度差值在10-2K以内，基本等于零件温度。

1.2.3 参数变化对结果的影响

从物性参数而言，本文研究对象为铸铝材质，热导率约为铸铁的3至4倍。因此应用集总热容法的前提条件对于铸铁仍待验证。现代发动机采用铝材的比例较大且处于上升趋势[8]，因此本研究的适用范围处于合理水平。充气参数和测试时间上，现有文献给出的数值与上文中零件的生产测试参数基本处于同一量级[4-5]。

从几何形态而言，需要进行泄漏测试的容积，包括水道、油道、气道等，属于工作压力较高、起传热或输运功能的容积，均具有容积较小、比表面积较大的特点。由于得出的压力和热平衡的结论能够在较大的参数变化范围内成立，因此研究成果适用于大多数同类型发动机零部件。

2 结论

通过对发动机零部件泄漏测试中，充气和稳压阶段的理论计算和数值模拟，证明了这一阶段结束时腔内气体足以达到温度和压力平衡，其后的测试阶段并不会受这一阶段充气温度和充气时间等参数的影响。测试阶段的温度变化和测试结果仅受到测试期间零件温度和环境温度的影响。

通过计算，证明了测试阶段零件作为一个整体符合应用集总热容法的条件，并计算得出零件温度和气体温度与时间呈负指数关系。对于较小的时间和温度范围，该关系曲线较为平缓，近似于线性规律。这一结论支持了现有研究中实验数据的分布规律，并对现有研究中，采用线性方程描述实验结果在温度范围增大时产生偏差的现象提供了解释。

研究成果给出了泄漏测试中各外部因素与结果误差的关系，从而为温度补偿方案设计中简化实验方案、扩大方案适用范围提供了方向和理论依据。

[1] 朱正德. 泄漏检测技术在现代汽车制造业中的应用[J]. 机械开发, 1999(3):30-35.

[2] 田广奎. 发动机气密性检测技术与温度补偿[J]. 现代零部件, 2012(7):64-67.

[3] 朱正德. 温度因素对密封性测试的影响及其应对技术措施[J]. 组合机床与自动化加工技术, 2012(8):85-88.

[4] MEURER K-H. 在自动化密封检验中对温度影响的补偿[J]. 组合机床与自动化加工技术, 1992(6):40-41，47.

[5] 李锦云, 朱会学, 马林. 压降检漏过程中温度对漏率检测影响研究[J]. 机床与液压, 2010,38(13):10-12，21.

[6] INCROPERA F P, DEWITT D P, BERGMAN T L, et al. Fundamentals of Heat and Mass Transfer[M]. INCROPERA F P, INCROPERA F P F O H A M T. Water, John Wiley & Sons, 2007, 6th: 997.

[7] 王普凯, 赵以贤, 毕小平，等. 基于集总参数法的车用内燃机传热计算机仿真研究[J].内燃机学报, 2003，21(4):239-243.

[8] 姜海涛, 王孟君, 黄电源. 汽车用铝合金的研究进展[J]. 金属热处理, 2006,31(9):34-38.

[9] 袁云峰. 温度补偿对零部件泄漏检测的精度控制[J]. 现代零部件, 2013(1):75-76.

[10] 刘洋, 张永娟, 纪春华，等. 基于数据融合的流量式泄漏检测温度补偿方法研究[J]. 液压与气动, 2010(10):52-55.

(编辑 李秀敏)

Analysis of Heat Transfer in Engine Leak Test

WANG Meng-zhe1,ZHANG Jun2,WANG En-lu1,WANG Li-fen1

(1.School of Mechanical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2.Shanghai General Motors Co.,Ltd.,Shanghai 201206,China)

Temperature difference in vehicle engine parts leak test can cause error in test results. Mathematical model is built and numerical simulation is applied separately for each procedure of leak test. Transient analysis of testing procedure is proceeded using lumped heat capacity method. The results shows that in the first procedure, charging and stabilizing, the tested capacity can achieve balance of temperature and pressure. During the second procedure i.e. testing procedure, the part and capacity temperature has a negative exponential relationship with testing time, which affects test results. In addition, the transient temperature pattern is provided for further analysis.

engine assembly line; leak test; temperature compensation; numerical simulation; lumped parameter method

1001-2265(2014)07-0066-04

10.13462/j.cnki.mmtamt.2014.07.018

2013-10-08；

2013-10-24

王勐喆(1988—)，男，甘肃天水人，上海交通大学硕士研究生，主要从事汽车动力总成装配线测试系统研究，(E-mail)wmz@sjtu.edu.cn。

TH122;TG65

A