基于网格变形技术和响应面模型的机床床身优化方法*
王万金,殷国富,胡 腾,姬坤海
(四川大学 制造科学与工程学院,成都 610065)
基于网格变形技术和响应面模型的机床床身优化方法*
王万金,殷国富,胡 腾,姬坤海
(四川大学 制造科学与工程学院,成都 610065)
针对数控机床的轻量化设计要求,提出了一种基于网格变形、响应面模型和多岛遗传算法集成的机床床身轻量化优化设计方法。将网格变形技术和基于响应面模型的优化技术相结合,开发了基于VC++的软件模块,将有限元模型转化为能够进行网格变形的动态分析模型。采用优化拉丁方对设计空间进行采样,获取相关变量的灵敏度,剔除低灵敏度变量后,拟合高精度二阶响应面模型。以多工况下床身导轨最大变形、首阶固有频率和床身体积作为评价指标,在保持动静态特性基本稳定的条件下,采用多岛遗传算法对近似模型进行轻量化优化设计。优化设计实例结果对比分析表明,所提出的优化方法可使某型精密卧式加工中心床身的质量减轻7.5%,取得了较好的优化设计效果。
网格变形;响应面模型;多岛遗传算法;床身
0 引言
精密卧式加工中心是我国航空航天、精密模具、汽车工业等制造行业领域的关键加工设备[1]。床身作为精密卧式加工中心重要部件之一,起支撑各种零部件的作用,其动静态性能的好坏直接影响到机床的工作性能。对于这类复杂的机械结构,目前国内外学者对其优化设计进行了大量的研究。文献[2]利用ANSYS 有限元分析软件, 研究了不同床身高度时床身固有频率的变化趋势, 以及筋板不同布置方式对床身动态特性的影响。这种设计方法的缺点是缺乏明确的理论指导, 依赖于设计者的经验,因此效率低下。为了避免机床设计过多依赖设计者的经验,文献[3]开发了优化设计平台,综合运用Pro/E对锻压机床进行参数化建模和MATLAB编写遗传算法,对锻压机床进行尺寸优化,确定了机床合理的结构尺寸。但是这种方法每优化迭代一次就需要求解新的有限元模型,耗时长,因此不适合用于大型复杂零件的优化设计。为了解决这一问题,Kogl 等[4]运用近似模型的优化方法,对车身结构进行多学科优化,以实现车身减重设计。文献[5]提出了一种将响应面模型与多目标遗传算法相结合的优化设计方法,用近似模型替代了有限元模型对某型机床立柱进行了优化,减少了优化求解时间。但是该方法在对样本点数值求解和验证在近似模型下获得最优解的立柱参数时,需要重新构建立柱三维模型和有限元模型,效率仍不够高。
基于上述问题的考虑,本文在参考文献[6]中利用商用软件DEP Meshworks/Morpher 网格变形技术对白车身多目标形状优化和综合上述各种优化求解方案的优点之后,提出了基于网格变形技术和响应面模型的床身优化设计方法。
1 优化模型
以某型精密卧式加工中心床身为研究对象,在实际装配边界条件下,以两种工况(限于篇幅两种工况具体加载未在本文中指出)下床身导轨最大变形、最大应力和首阶固有频率作为床身动静态特性评价指标,进行有限元分析,得到以下结论:①最大应力(17.6MPa)远小于材料许用应力(120MPa)②床身筋板主要有两种厚度20mm和25mm,某些筋板厚度改变之后基本上不会造成动静特性降低。故可以对床身筋板厚度进行尺寸优化。床身简化模型如图1所示,床身内部筋板布局如图2所示。
根据上述分析,确定了以床身体积最小为目标,以考虑多工况下床身导轨最大变形和首阶固有频率基本稳定为约束条件的优化模型。
优化数学原模型表述如下:
其中volume为床身体积,Disp_1为工况1最大变形上限,Disp_2为工况2最大变形上限,Freq_1为首阶固有频率下限,X为床身内部各处筋板厚度的增量值,x1b,x2b,,,x9b为设计变量下限值,x1u,x2u,,,x9u为设计变量上限值。
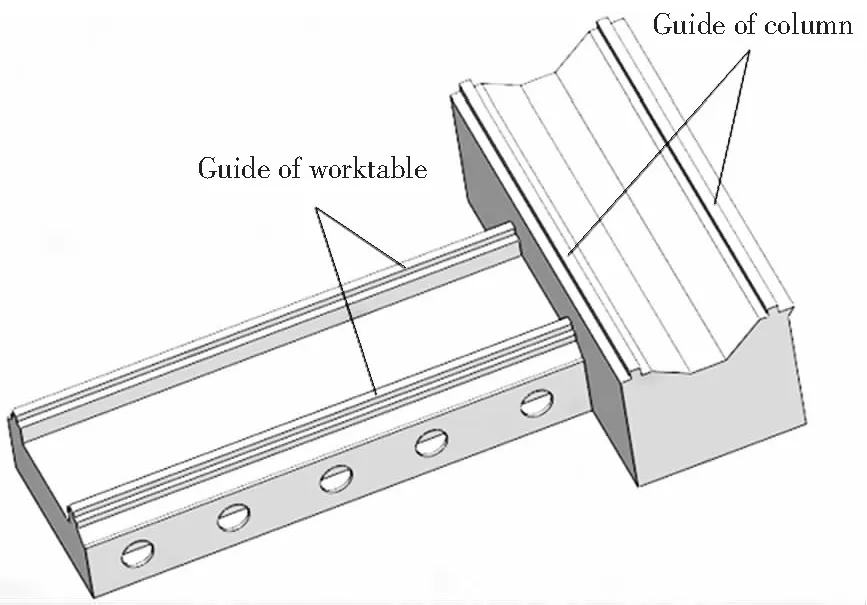
图1 床身简化模型图
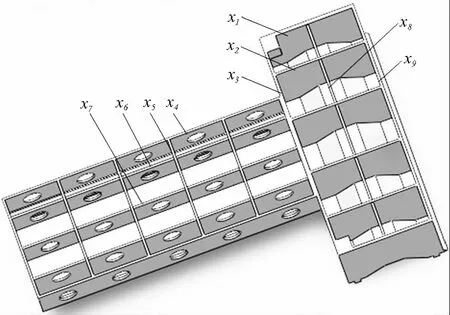
图2 床身内部筋板布局图
2 优化流程
具体流程叙述如下:
步骤1:利用HyperMesh中的ANSYS模板对床身划分网格和加载,得到求解的原始有限元模型;接着对原始有限元模型中需要变形的网格节点集分别平移特定值(注:这里约定特定值分别为0.0005、0.0010、0.0015…,一个特定值代表一个变量),得到修改有限元模型。
步骤2:利用自行开发的软件对原有限元模型和修改有限元模型进行对比,提取出变量值,得到具有网格变形的动态分析模型。
例:原有限元网格中节点坐标为N,1,1.0,1.0,1.0,修改有限元网格中节点为N,1,1.0,1.0,1.001;那么,经过软件对比处理后,得到具有网格变形的节点坐标为N,1.0,1.0,1.0+x2(注:x2为变量)。
步骤3:用ANSYS对原有限元模型求解,将得到的多工况下床身导轨最大变形和首阶固有频率作为优化求解的约束条件的上下限值。
步骤4:对优化模型进行试验设计,得到各个变量的灵敏度,为建立响应面模型做准备。
步骤5:对试验设计得到的各变量的灵敏度进行分析,踢出灵敏度低的变量,建立响应面模型。
步骤6:利用多岛遗传算法对步骤5建立的响应面模型进行优化。
步骤7:对步骤6中得到优化结果进行数值求解,判断其是否满足优化要求,若满足优化要求,则判断是否满足收敛准则;若不满足优化要求或者不满足收敛准则,则将优化结果的数值求解值增加至样本点,更新响应面模型,重复步骤5~步骤7。
具体流程图如图3所示。
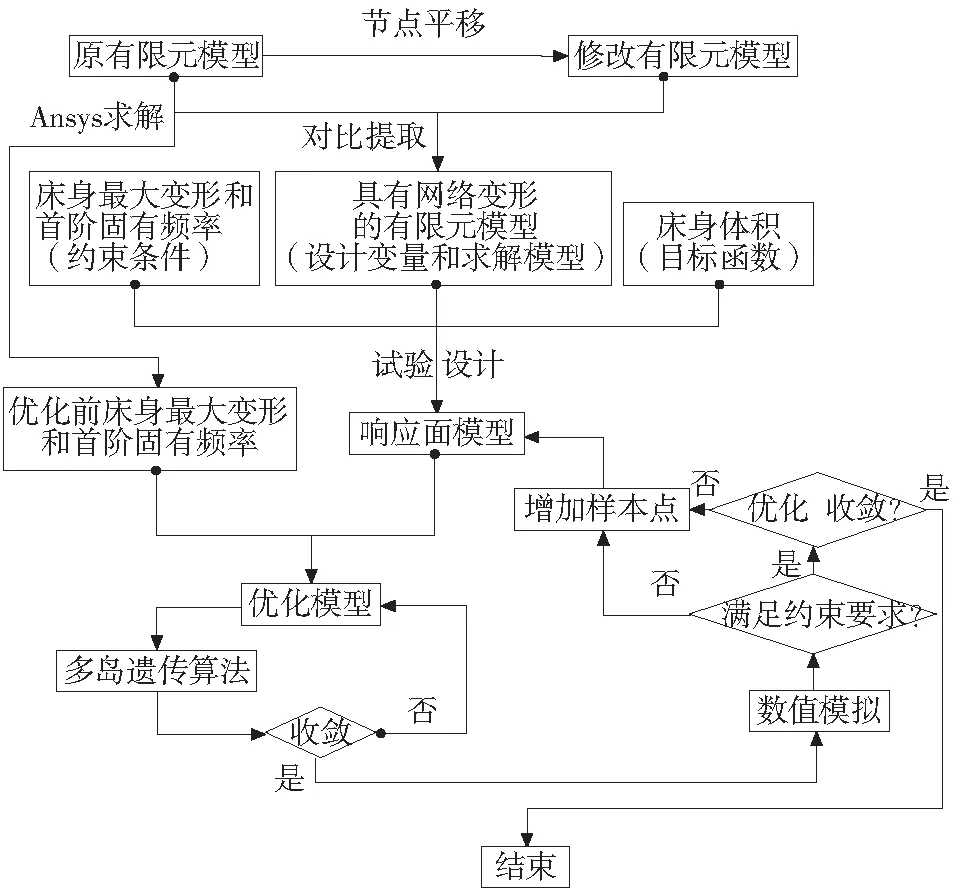
图3 优化流程图
3 网格变形
有限元模型的网格变形的实质是网格中的节点按照给定的表述形式进行移动。这种表述形式既可以是数学表达式,也可以是自由目标形状定义的几何形式[7]。文中由于只是对筋板厚度的尺寸进行优化,所以只涉及到节点的平移,如图4所示。通过网格的变形,避免了传统优化方法中每次优化迭代后重新构建CAD模型和CAE模型,提高了优化求解效率。
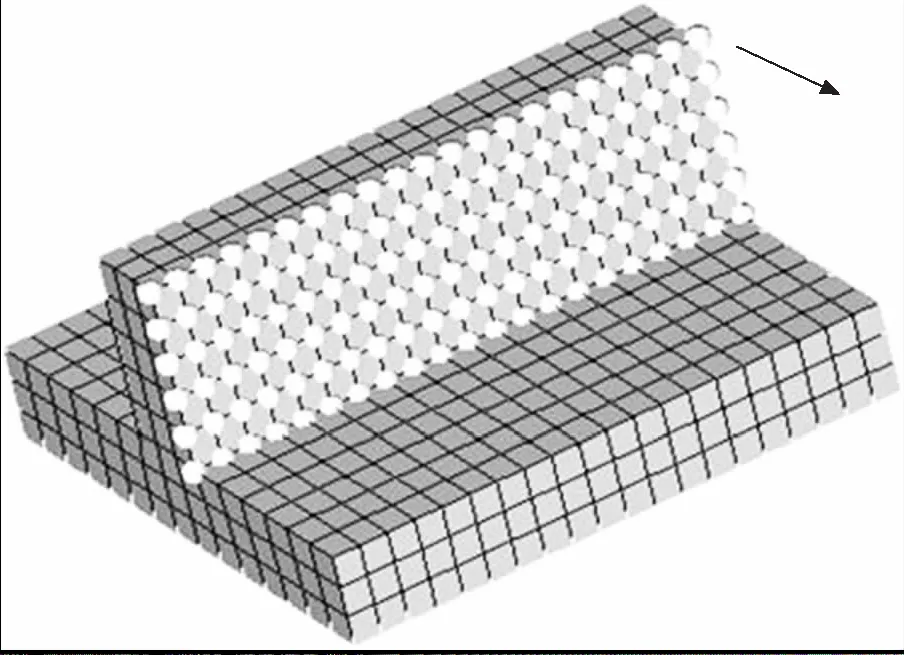
图4 节点集移动示意图
4 响应面模型
响应面法(RSM)的实质是构造一个近似表达式来替代原模型中设计变量与约束条件以及目标函数之间的复杂映射关系。该方法将试验设计与数理统计相结合,可以全面观察响应变量在设计空间的变化[8]。响应面模型的构造主要包括:①试验设计,即从设计空间中选择能构建响应面模型足够数量的样本点。②将试验设计得到样本点进行数值求解,并将求解结果进行数据拟合,建立响应面模型。
4.1 试验设计
要建立高精度的响应面模型绝大程度取决于能否对设计空间进行合理均匀采样。目前应用最多的采样方法是拉丁方采样,但是这种方法是一种随机均匀采样方法,它的随机性使得采样的均匀程度不够好。本文选择Jin等[9]提出的优化拉丁方进行空间采样。该方法是拉丁方的改进采样方法,它从一个随机的Latin Hypercube matrix开始,通过优化输入采样点的空间分布,使得设计点在空间尽可能地均匀分布,如图5所示。
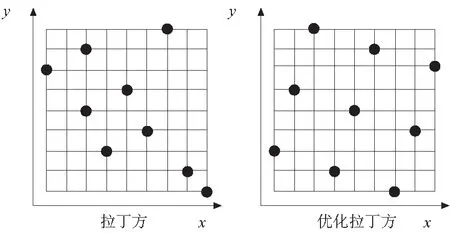
图5 拉丁方采样与优化拉丁方采样对比示意图
为了建立二阶响应面模型,最小采样数目是(N+1)×(N+2)/2,其中N为试验变量的个数。此外,在设计空间内采样点的个数越多,响应面模型拟合精度就越高。文中总共9个设计变量,为了保证响应面模型足够的精度,最小样本数目是55个,本文取110个样本,用优化拉丁超立方生成9×110的样本矩阵,如表1所示,其中第16个样本所得到的体积最小。
4.2 响应面模型的建立
在建立响应面模型之前,要对试验设计获得的各个变量的灵敏度进行分析,踢出影响小的变量,保留影响大的变量,然后再进行响应面模型的拟合。本文采用具有较高准确性的二阶多项式响应面拟合模型,n个设计变量的二阶多项式响应面模型可表示为[5]:
其中y为响应量;x为设计变量;β为回归系数,可用最小二乘法拟合回归得到。
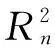
为了对近似模型进行误差检验,本文取50个点进行误差计算。图6为近似模型的总误差图,最大总误差不超过1%。由此可见,近似模型对实际模型的预测精度高。
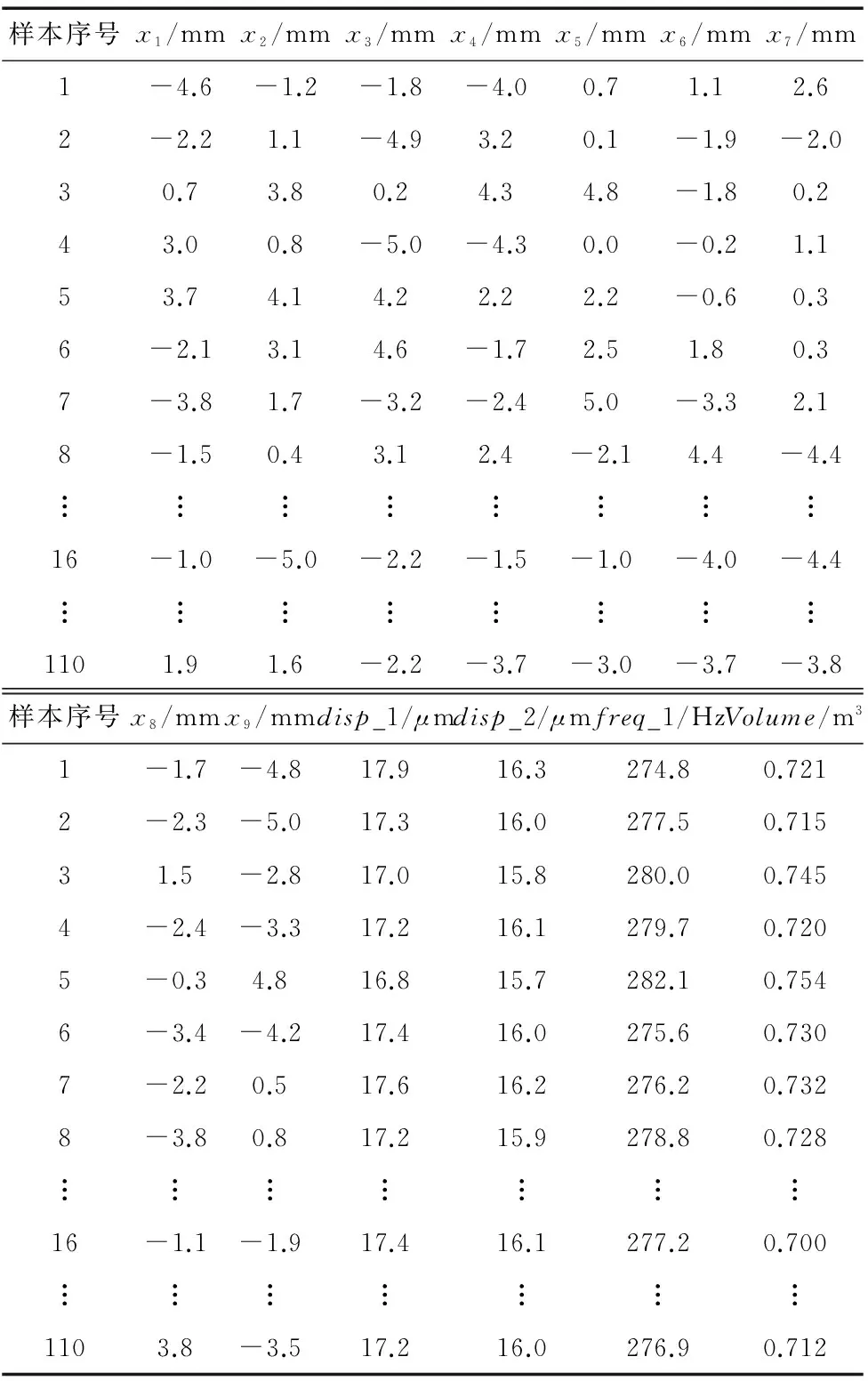
表1 试验设计方案及评价指标样本
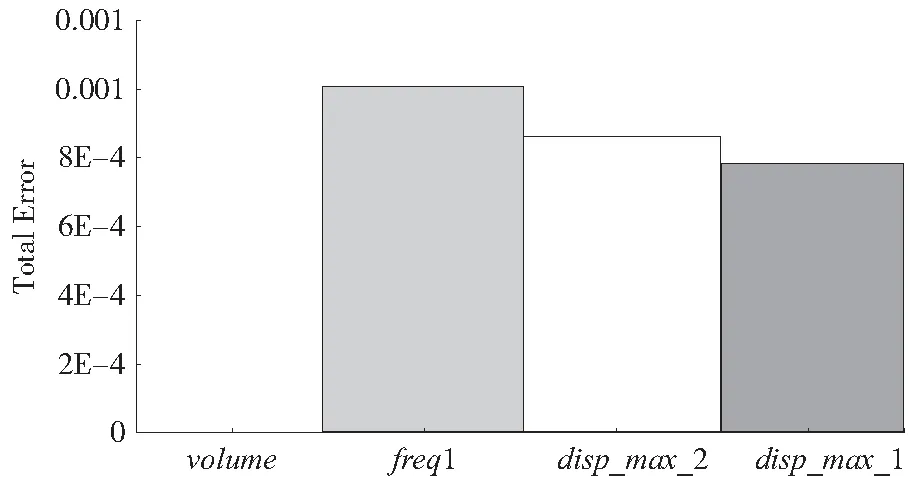
图6 各个响应的总误差图
5 优化算法
从上文的分析可知,机床床身结构的最优尺寸是9个筋板厚度的典型组合问题,优化求解可能存在多峰问题。因此,优化求解算法必须是全局探索方法。常用的全局探索法有遗传算法和自适应模拟退火算法等。
遗传算法是一类模拟生物界自然选择和遗传的启发式随机搜索算法,能同时对搜索空间中的多个点进行评估,具有较好的全局搜索性能,减少了陷于局部最优解的风险。由于遗传算法具有简单通用、鲁棒性强、适用于并行处理等显著特点[11],其在机床优化方面得到了广泛应用。但是传统的遗传算法,由于参与遗传进化的种群的单一性,使得其在优化上容易陷入早熟[12]。为了解决这一问题,在传统的遗传算法的基础上,发展了众多改进算法,其中一种是多岛遗传算法。多岛遗传算法与传统的遗传算法不同之处在于增加了岛屿,将原来的单一种群,分成多个子种群,遗传进化在子种群中进行,子种群之间存在定期迁徙,如图7所示。多岛遗传算法的迁徙操作保持了解的多样性,提高了包含全局最优解的机会,可抑制早熟现象的发生。
本文选择多岛遗传算法作为优化方法,具体参数设置如表2。
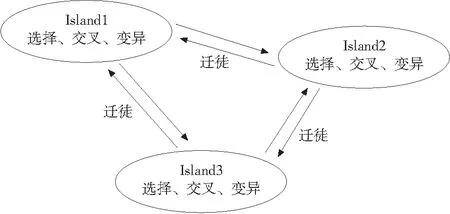
图7 多岛遗传算法示意图表2 多岛遗传算法参数设置

每个岛屿中个体数目岛屿个数进化代数迁移率迁移间隔交叉概率变异概率502100.520.90.01
经过多岛遗传算法对近似模型和实际模型的组合优化迭代1000次之后得到最优解,如表3所示。由表可知,优化后多工况下的最大变形和首阶固有频率变化很小,而机床体积减少了7.5%,机床床身轻量化优化设计效果明显。

表3 优化前后设计变量及评价指标
6 结论
本文以某型精密卧式加工中心床身的优化设计为应用实例,提出了一种基于网格变形、响应面模型和多岛遗传算法集成的机床床身轻量化优化设计方法。该方法通过运用网格变形技术,避免了每次优化迭代后复杂三维模型的重构,提高了优化的效率。为了寻找最优筋板尺寸,引入多岛遗传算法,考虑到全局探索的优化迭代计算次数量十分庞大,引入响应面模型来近似替代有限元模型,缩短了计算时间。故该方法与目前机床结构优化中普遍采用的基于多次数值分析的方案优选法相比,具有较好的计算精度和较高的计算效率。该方法也适合于机床中其他类似零部件的优化问题。
[1] 巫修海,马云芳,张建润. 高速高精度卧式加工中心动态优化设计[J]. 振动与冲击,2009,28(10):74-77.
[2] 李小彭, 赵志杰, 聂慧凡, 等. 某型数控车床床身的模态分析与结构优化[J]. 东北大学学报(自然科学版),2011, 32(7):988-991.
[3] 申远金, 褚彪, 骆念武, 等. 基于遗传算法的锻压机床多目标优化设计方法[J]. 中国机械工程,2012,23(3):291-294.
[4] Kogl M, Klimetzek F R, Pletschen B, et al. Multidisciplinary Optimization of Body-in-white[J]. Simvec-Numerical Analysis and Simulation in Vehicle Engineering, 2008, 2031:721-744.
[5] 于海莲, 王永泉, 陈花玲, 等. 响应面模型与多目标遗传算法相结合的机床立柱参数优化[J]. 西安交通大学学报,2012,46(11):80-85.
[6] 方剑光, 高云凯, 王婧人, 等. 基于网格变形技术的白车身多目标形状优化[J]. 机械工程学报,2012,48(24):119-126.
[7]Auweraer H Van der, Langenhove T V, Brughmans M, et al. Application of Mesh Morphing Technology in the Concept Phase of Vehicle Development[J]. International Journal of Vehicle Design, 2007, 43:281-305.
[8] 伊卫林, 黄鸿雁, 韩万金. 基于模拟退火算法与响应面模型的三维气动优化设计方法[J]. 空气动力学学报,2008,26(1):36-41.
[9]Jin R, Chen W, Sudjianto A. An Efficient Algorithm for Constructing Optimal Design of Computer Experiments[J]. Journal of Statistical Planning and Inference, 2005, 134(1):268-287.
[10]Wei S, Nilay P, Rajkumar V, et al. Global Design Optimization for Aerodynamics and Rocket Propulsion Components[J]. Progress in Aerospace Sciences, 2001, 37(1): 59-118.
[11] 王小平, 曹立明. 遗传算法—理论应用与软件实现[M]. 西安: 西安交通大学出版社, 2003.
[12] 牟淑志, 杜春江, 牟福元, 等. 基于多岛遗传算法的连续体结构拓扑优化[J]. 机械科学与技术,2009,28(10):1316-1320.
(编辑 李秀敏)
Optimization Method for the Bed Structure of Machine Tool Based on Mesh Morphing and Response Surface Model
WANG Wan-jin,YIN Guo-fu,HU Teng,JI Kun-hai
(College of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065,China)
Aiming at the purpose of lightweight design for machine tool, an optimization approach which was integrating mesh morphing technology(MMT) with response surface model(RSM) and multi-island genetic algorithm(MIGA), was proposed for lightweight design of machine tool bed. Combining MMT and optimization technology based on RSM, a software module based on VC++ was developed to convert original finite element model(FEM) into a dynamic FEM that was capable of mesh morphing. An optimal Latin hypercube was employed to sample the design space, and to obtain sensitivities of the variables. After eliminating the insensitive variables, a second-order RSM was constructed. MIGA was adopted to execute the optimization procedure, where the minimum volume of the bed was regarded as object function, and the stabilization of its maximum deformation and 1st-order natural frequency were regarded as constraint conditions. A conclusion can be drawn that the proposed approach performs a good optimization for the machine center bed which is lightened by 7.5%.
mesh morphing; response surface model; multi-island genetic algorithm; bed
1001-2265(2014)07-0005-04
10.13462/j.cnki.mmtamt.2014.07.002
2014-01-09
国家科技重大专项"高档数控机床与基础制造装备"课题 (2013ZX04005-012)
王万金(1989—),男,四川简阳人,四川大学硕士研究生,主要研究方向为机床结构优化、数字化设计,(E-mail)wwj1234567@yeah.net;通讯作者:殷国富(1956—),男,成都人,四川大学教授,博士研究生导师,主要研究方向为制造自动化、智能设计技术、CAD/CAM/CIMS,(E-mail)gfyin@scu.edu.cn。
TH122;TG65
A

