车轮扁疤引起的轮轨冲击分析

王忆佳，曾京，高浩，罗仁

(西南交通大学牵引动力国家实验室，四川 成都 610031)

自时速200 km/h的CRH系列动车组开行以来，我国高速铁路得到了迅猛发展.高速动车组虽然采用了先进的防滑和防空转技术，车轮和钢轨的擦伤已减少到较低水平，但车轮擦伤是不可避免的，这是世界各国铁路普遍存在且难以解决的问题，车轮擦伤问题不仅困扰车辆运行部门，且会给钢轨、轨枕等带来伤害.轮轨间的垂向冲击作用，是限制机车车辆轴重增大和列车速度提高的关键因素.因此，研究车轮擦伤及其引起的动力学问题很有现实意义，已经引起了不少学者的关注.

车轮扁疤是踏面擦伤、剥离、缺损、熔渣等影响车轮滚动圆圆度造成车轮周期性撞击钢轨故障的统称.随着车轮的旋转，发生扁疤的车轮在列车行驶过程中对轮轨产生间歇性的脉冲激扰源，当车轮滚至扁疤处时，产生的冲击力比平时大几倍，有时甚至十几倍.Newton［1］较早的给出了扁疤导致的冲击载荷的研究方法，同时将扁疤数学模型的计算结果与试验结果进行了比较.Newton与Clark［2］将扁疤冲击效应等效为轨道低接头冲击效应，认为车轮运行至扁疤处引发的冲击与无扁疤车轮运行至轨道低接头引发冲击的轮轨动力学模型上是相同的，并根据低接头冲击模型导出扁疤冲击力计算公式.Wu和Thomson［3］研究扁疤冲击引发的轮轨噪声问题时，也在动力学模型上将扁疤等效为轨道周期不平顺.

国内许多学者对扁疤信号的检测做了大量研究，也有学者对扁疤冲击引起的轮轨噪声进行探索性研究.王建斌等［4］利用简化的扁疤冲击力公式，给出了含扁疤冲击时车轴危险截面的应力谱.翟婉明［5］建立了轮轨系统垂向模型，并用其所编制的VICT软件进行了扁疤冲击响应的仿真计算，给出货车扁疤长度限值.刘建新等［6］分析了重载车辆车轮踏面擦伤时轮轨系统动态作用特征.就车轮扁疤引起的轮轨冲击问题而言，传统等效轨道激扰法是将车轮扁疤等效为轨道上的周期激扰，并没有考虑车轮半径变化对轮轨接触几何关系的影响，无法准确的计算车轮扁疤引起的轮轨冲击力.

本文在上述文献的基础上，针对我国高速车辆，对车轮扁疤仿真模型进一步改进，建立了车辆系统整车动力学模型，采用变化车轮半径的方法模拟车轮扁疤，同时考虑车轮半径对轮轨接触状态和接触参数的影响，研究车轮新旧、扁疤引起的轮轨冲击力的变化规律，给出高速车辆车轮扁疤的安全限值.

1 车辆系统动力学建模及扁疤模型

1.1 车辆系统动力学模型

本文应用多体系统动力学理论，建立了高速车辆非线性系统动力学仿真模型.模型由1个车体、2个构架、4个轮对和8个轴箱、一系悬挂和二系悬挂组成多刚体系统.一系悬挂装置采用双拉杆轴箱定位方式，安装垂向减振器和钢弹簧;二系悬挂安装有摇枕、抗侧滚扭杆、空气弹簧、横向减振器、垂向减振器、横向止挡、抗蛇行减振器等.车体、构架和轮对各考虑6个自由度，轴箱考虑1个自由度，系统共计15个刚体，50个自由度.模型中考虑了悬挂系统以及轮轨接触的非线性，建立的车辆系统动力学方程的一般表达式为

式中:

q为车辆系统广义坐标;

t为运行时间;

M、C、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;

Fn(˙q，q，t)为非线性力元引起的广义力向量;

Fc(˙q，q，t)为轮轨接触力广义力向量，包括由轮轨法向力和轮轨蠕滑力［7］.

轨道模型为离散的刚性轨道模型，直接固定在惯性坐标系中，通过垂向刚度、横向刚度和阻尼元件弹性的连接在轨道坐标系上，轨道具有与车轮相关方向上的质量和惯性.在非线性接触关系中，轮轨接触几何参数是轮对横移量的非线性函数，包括车轮滚动圆半径、车轮横断面曲率半径、轮对侧滚角、接触角.车轮扁疤所导致车轮半径在周向不再为定值，而是随车轮不同周向角度发生变化.因此，本文采用如车轮踏面一样的描述方式，用车轮周向半径描述文件描述车轮扁疤.传统的查表法计算轮轨接触几何关系不再适用，本文采用轮轨接触几何参数实时计算，根据轮对滚动角度，查找当前接触点对应的车轮半径和其他轮轨接触参数.轮轨间的蠕滑力由Kalker非线性蠕滑理论计算.考虑扁疤的车辆系统动力学仿真流程如图1所示.

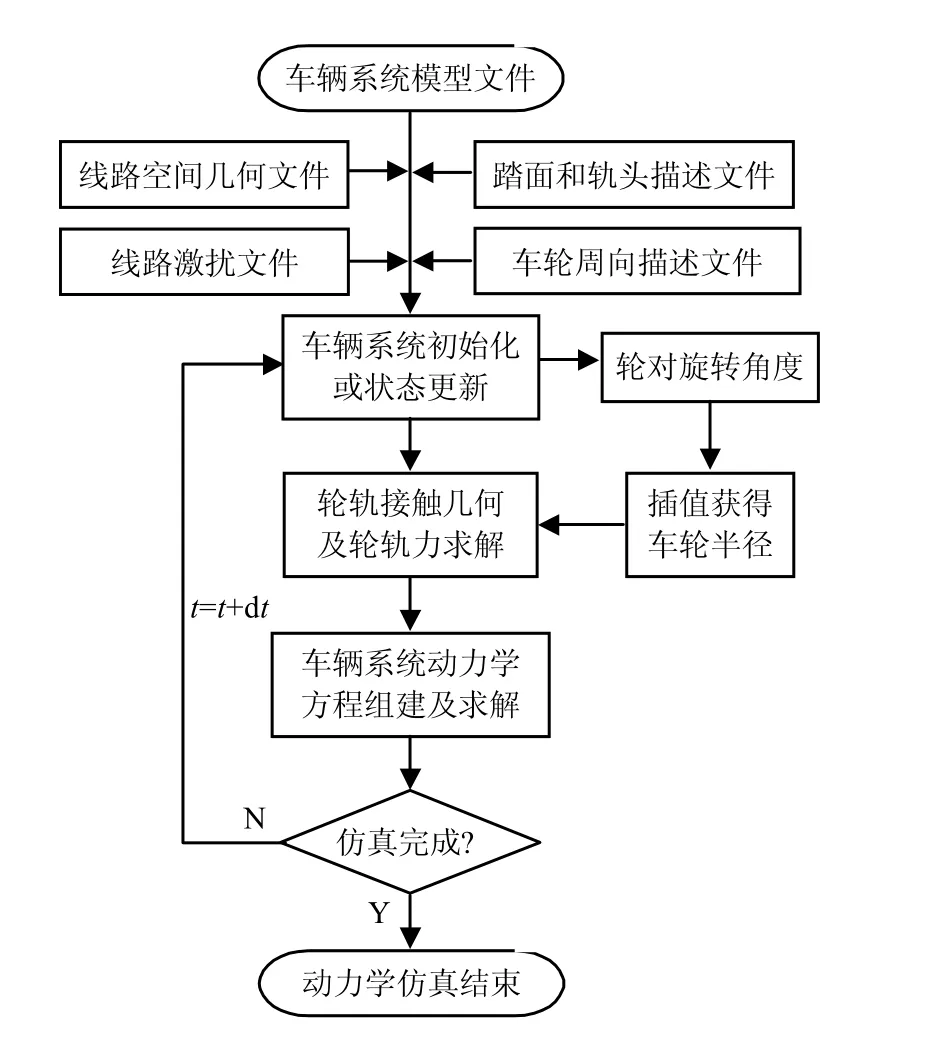
图1 考虑扁疤的车辆系统动力学仿真流程Fig.1 Flow chart of vehicle dynamics simulation with wheel flats

1.2 车轮扁疤模型

当车辆轮对制动或空转时(特别是发生车轮抱死时)，车轮容易产生擦伤，并在车轮踏面上形成一块扁疤.随着车轮的旋转，扁疤将对轮轨系统造成周期性的冲击作用.这种冲击载荷通过轮对传递到车辆的关键部件，如齿轮箱和电机等，引起车辆的动态运行特性发生改变.由于新、旧擦伤车轮对线路的动力学效应是迥然不同的，两种仿真分析模型也存在差异，所以本文分别从新扁疤和旧扁疤角度，通过仿真计算来分析轮轨系统的冲击振动.新、旧扁疤的示意如图2所示，图中:L0为旧扁疤长度;Ln为新扁疤长度;h为擦伤深度.

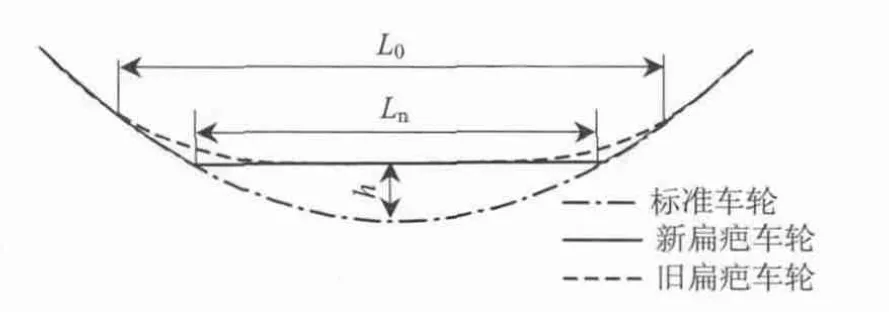
图2 扁疤形状Fig.2 Geometry of wheel flats

1.2.1 车轮新扁疤模型

文献［8］中对车轮新扁疤冲击机理做了详细的论述，理想的新擦伤类似于车轮踏面圆周上的弦线.对高速车辆而言，由于车速较快，擦伤面可能接触不到轨面，而在擦伤端点处撞击钢轨形成冲击.经过推导，得到高速时的车轮冲击速度为

式中:

L为扁疤长度;

R为车轮半径;

v为车速;

γ为车轮旋转惯量转换为往复惯量的系数;

μ=(M1+M2)/(M2g)，

其中，M1、M2分别为车辆一系簧上、簧下质量，g为重力加速度.

由式(2)可见，高速时的扁疤冲击速度也与扁疤长度成正比，但随速度增加而略有下降，最终趋于恒定值为

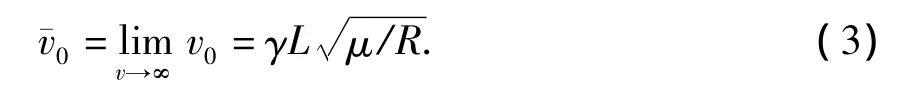
1.2.2 车轮旧扁疤模型

车轮扁疤取决于扁疤长度和车辆速度，有效的擦伤形状对于产生的冲击载荷峰值影响较大.在实际运营中，理想新擦伤并非经常出现，一旦出现，经过一段时间运行后，车轮踏面擦伤棱角受冲击荷载作用很快被磨圆，俗称旧扁疤.用lyon扁疤冲击激扰模型表示［9］.

扁疤不平顺公式为［4］

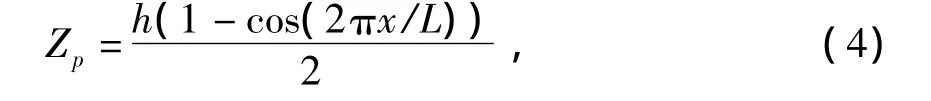
式中:h=L2/(16R);

x为沿车轮表面的弧长.

将扁疤深度与扁疤长度的关系折算为扁疤深度与旋转角度之间的关系，用车轮半径减去扁疤深度得到旧扁疤的车轮周向半径.

不同扁疤长度的外形如图3所示.

图3 车轮旧扁疤的外形Fig.3 Profile of old wheel flats

2 轮轨冲击振动

文献［10-11］中认为车轮通过轨道低接头时，轮轨间动态接触力会出现两个峰值:力P1和力P2.文献［12-13］中的理论计算和实验也反应出这一规律.

图4为脉冲激扰下的轮轨垂向冲击力响应，是典型的轮轨垂向冲击力波形.

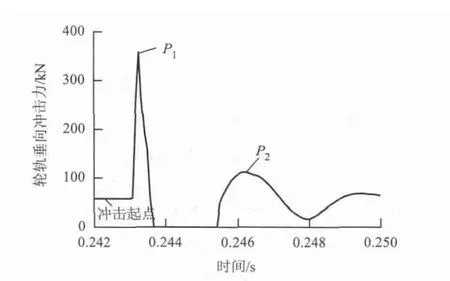
图4 脉冲激扰下的轮轨垂向冲击力响应Fig.4 Responses of vertical impact force under impulsive excitations

2.1 新扁疤模型仿真分析

在扁疤长度一定时，轮轨垂向力随着车速增大先增大后减小，当车速为50 km/h时，P1、P2均达到最大，如图5所示，这一结果与理论相符.当车速一定，随着扁疤长度增大，P1、P2均增大，如图6所示.

从图7可以看出，P1随着车速的增大，先增大后减小，当扁疤长度小于等于 30 mm，车速为50 km/h时，P1最大;当扁疤长度大于30 mm车速为100 km/h时，P1最大，达到350 kN.如图8所示，P2的基本趋势与P1相仿，都随着车速的增高而先增大后减小，当车速为50 km/h时最大.

图5 车速对扁疤轮轨垂向冲击力的影响(新扁疤)Fig.5 Influence of train's running speed on wheel/rail vertical impact due to new wheel flats

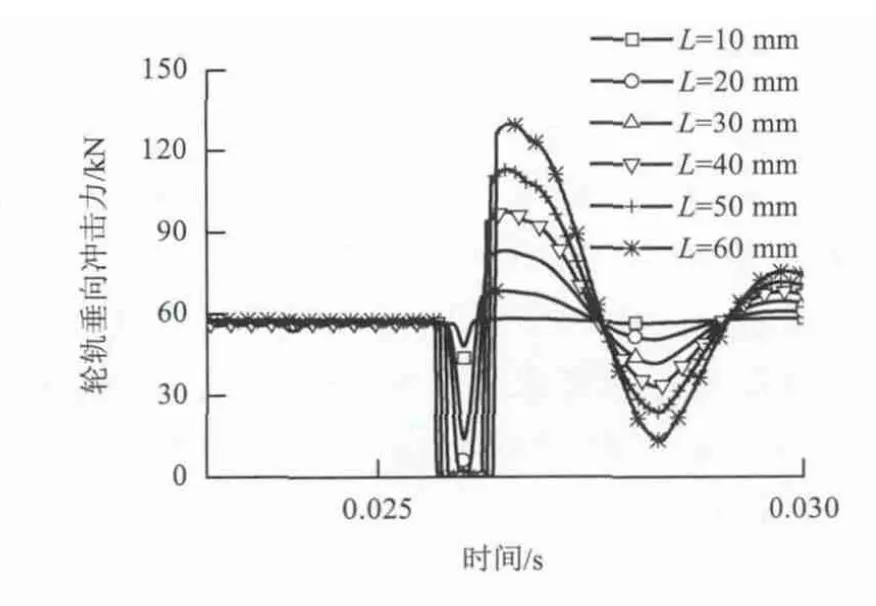
图6 扁疤长度对轮轨垂向冲击力的影响(新扁疤)Fig.6 Influence of flat length on wheel/rail vertical impact due to new wheel flats

图7 车速对P1的影响(新扁疤)Fig.7 Influence of train speed on wheel/rail vertical force P1under new wheel flats

图8 车速对P2的影响(新扁疤)Fig.8 Influence of train speed on whee/rail vertical force P2under new wheel flats

2.2 旧扁疤模型的仿真分析

通过仿真计算，比较扁疤长度和车速对轮轨冲击力和振动加速度的影响.图9为扁疤长度为30 mm，不同车速下的轮轨垂向冲击力.

从图9中可以看出，轮轨垂向力随着车速的增高而增大，但车速为250 km/h时，P1最大，车速为50 km/h时，P2最大.

图9 车速对扁疤轮轨垂向冲击力的影响(旧扁疤)Fig.9 Influence of train speed on wheel/rail vertical impact due to old wheel flats

图10为车速300 km/h下，不同扁疤长度下的轮轨垂向力.从图10可以看出，P1、P2均随着扁疤长度的增大而增大.

对于旧扁疤模型，P1随着车速和扁疤长度的增大呈线性增大的趋势，如图11所示.P2随车速的增大先增大后趋于恒定值，当车速为50 km/h时，P2最大，如图12所示.

比较新扁疤和旧扁疤的P1和P2，由车速的变化规律可知，旧扁疤产生轮轨垂向冲击力将对高速车辆轮轨系统的危害更大.而新扁疤会发展成旧扁疤，因此要在扁疤发展到一定程度时对车轮进行镟修.高速车辆扁疤长度限值计算时也应该采用旧扁疤模型.

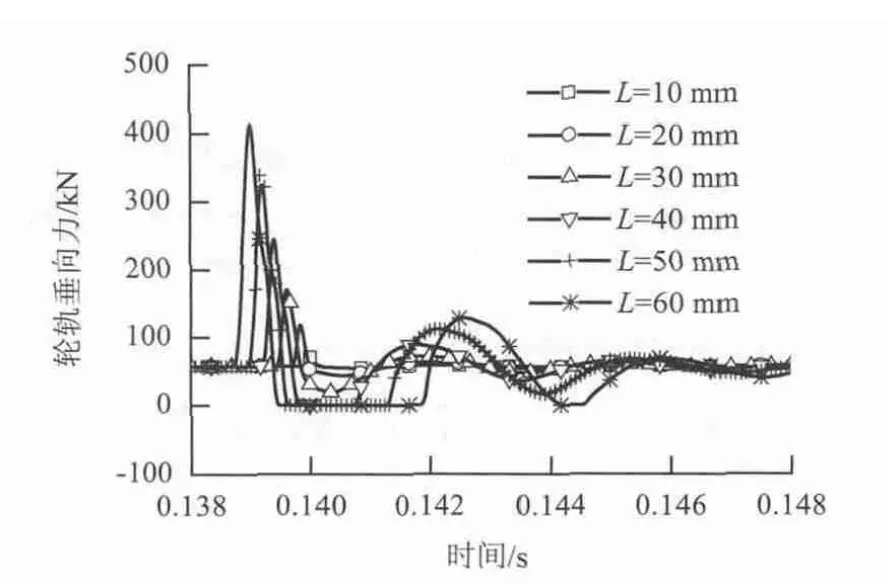
图10 扁疤长度对轮轨垂向冲击力的影响(旧扁疤)Fig.10 Influence of flat length on wheell/rail vertical impact due to old wheel flats

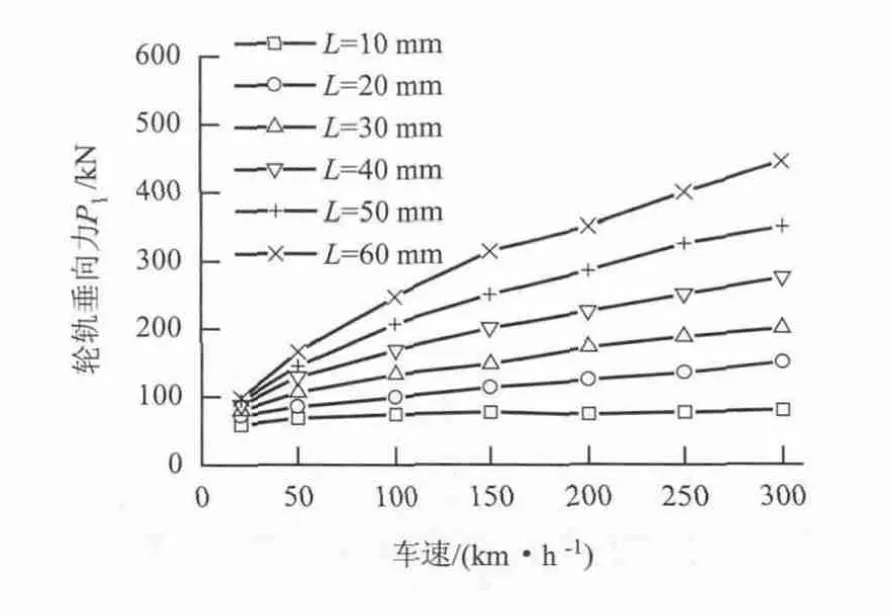
图11 车速对P1的影响(旧扁疤)Fig.11 Influence of train speed on wheel/rail vertical force P1under old wheel flats

图12 速对P2的影响(旧扁疤)Fig.12 Influence of train speed on wheel/rail vertical force P2under old wheel flats

3 安全限值

P1和P2是评价轮轨垂向相互作用的重要指标，也是设计机车车辆走行部分和选择轨道结构参数时重要参考依据.目前，关于轮轨垂向作用力.一般沿用英国铁路所定义的P1、P2作为衡量车辆对线路动力破坏效应的指标.各国的铁路具体条件不尽相同，尚无统一的限定值标准.我国铁标TB10621—1999《高速铁路设计规范(试行)》对250 km/h线路，垂向设计载荷按静载荷的2.5倍考虑;对300 km/h高速客运专线，垂向设计载荷按静载荷的3倍考虑.由于轮轨垂向力没有明确规定采样频率和滤波频率，现在我国的轮轨力检测方法还不能准确的测量得到P1和P2.以上规定只能作为参考.

根据国内外铁路的规定，应对高速车辆车轮扁疤做出以下限制.

考虑到一般不会出现理想的新扁疤，且在高速条件下旧扁疤的作用力远大于新扁疤，因此，本文采旧扁疤模型作为扁疤限制的计算模型，计算不同扁疤长度在不同车速下的轮轨垂向冲击力.参考我国《高速铁路设计规范》，以170 kN作为P1的限定值(P2幅值较小，不做评判)，计算结果如图13所示.由图13可知，当车速高于200 km/h时，车轮扁疤长度需要限制在35 mm以内;当车速高于250 km/h时，车轮扁疤长度需要限制在30 mm以内.

图13 扁疤安全限值Fig.13 Safety limits of wheel flats

4 结论

建立了50自由度车辆系统模型和新、旧两种扁疤冲击模型，采用轮径变化扁疤模拟法考虑了轮径对轮轨接触几何的影响，与传统的等效轨道激扰法相比，轮轨接触状态更加合理，轮轨力计算结果更准确.通过仿真分析得到扁疤冲击的基本规律，得到如下结论:

(1)旧扁疤产生轮轨垂向冲击力随车速增大而增大，在高速条件下远大于新扁疤产生的垂向冲击力.新扁疤会发展成旧扁疤，因此，扁疤发展到一定程度时需要对车轮进行镟修.

(2)以170 kN作为轮轨垂向力P1的限制值，当车速高于200 km/h时，车轮扁疤长度需要限制在35 mm以内.当车速高于250 km/h时，车轮扁疤长度需要限制在30 mm以内.

［1］NEWTON S G.An iterative procedure for the oscillatory laminar boundary layer［J］. International Journal for Numerical Methods in Engineering，1973，5(3):49-52.

［2］NEWTONS G，CLARK R A.An investigation into the dynamic effects on the track of wheel flats on railway vehicles［J］. Journal of Mechanics Engineering Science，1979，21:287-289.

［3］WU T X，THOMPSON D J.A hybrid model for the noise generation due to railway wheel flats［J］.Journal of Sound and Vibration，2002，251(1):115-139.

［4］王建斌，邬平波，唐兆.车轮扁疤引发附加冲击力对车轴应力谱影响的计算［J］.铁道学报，2006，28(1):39-43.WANG Jianbin，WU Pingbo，TANG Zhao.Research on the axle stress spectrum considering extra［J］.Journal of the China Railway Society，2006，28(1):39-43.

［5］翟婉明.铁路车轮扁疤的动力学效应［J］.铁道车辆，1994(7):1-5.ZHAI Wanming.The effect of wheel flat on vehicle dynamic performance［J］.Rolling Stock，1994(7):1-5.

［6］刘建新，易明辉，王开云.重载铁路车轮踏面擦伤时的轮轨动态相互作用特征［J］.交通运输工程学报，2010，10(3):52-56.LIU Jianxin，YI Minghui，WANG Kaiyun.Characteristic of dynamic interaction between wheel and rail due to wheel tread flat on heavy haul railway［J］.Journal of Traffic and Transportation Engineering，2010，10(3):52-56.

［7］WICKENS A H. Fundamentals of railvehicle dynamics［M］. Leicestershire:Swets ＆ Zeitlinger Publishers，2003:21-31.

［8］翟婉明.车辆-轨道耦合动力学［M］.3版.北京:中国铁道出版社，2007:55-62.

［9］DEREK L.Review of vertical dynamic track forces［R］.London:Office of Rail Regulation，2002.

［10］JENKINS H H，CLAYTON G A，MORLAND G W，et al.The effect of track and vehicle parameters on wheel/rail dynamic forces［J］. The Railway Engineering Journal，1974，3(1):2-16.

［11］LYON D.The calculation of track forces due to dipped rail joints［R］.Derby:BR Tech.，1972.

［12］张立民，张卫华.轮轨波磨形成机理与再现试验［J］.西南交通大学学报，2005，40(4):435-439.ZHANG Limin，ZHANG Weihua. Mechanism and experimental formation of wheel/rail corrugation［J］.Journal of Southwest Jiaotong University， 2005，40(4):435-439.

［13］MAIR W A，STEWART A J.The flow past yawed slender bodies with and without ground effects［J］.Journal of Wind Engineering and Industrial Aerodynamics，1985，18:301-328.

［14］JOHANSSON A，NIELSEN J C O.Out-of round railway wheels-wheel-railcontact forces and track response derived from field tests and numerical simulation［J］.Journal of Rail and Rapid Transit，2003，217:135-146.

［15］NIELSEN J C O，JOHANSSON A.Simulation of dynamic train-track interaction with state-dependent track properties［J］.Journal of Sound and Vibration，2004，275:515-532.