深水铺管船推力分配策略研究

姚明捷，许鹏鹏

（南通中远川崎船舶工程有限公司 技术部，江苏 南通 226005）

0 引言

船舶动力定位技术近年来在国内外发展十分迅猛，在军民用特种船舶上获得了较为广泛的应用，自1977年挪威船级社发布了船舶动力定位规范后，在20世纪90年代中后期，国外各大船级社均先后制定了相应的规范。随着动力定位技术的发展，动力定位的概念也在逐步扩大，动力定位/动态跟踪（Dynamic Positioning&Dynamic Tracking，简称“DP/DT”）作为一种高新技术在应用中越来越受到人们的重视。在船舶动力定位系统中，传感器测得对象船舶的位置和艏向角，之后与设定值进行运算比较，将位置及艏向角的偏差输入到控制器，控制器通过运算产生控制指令，经过推力分配，传达到执行机构，推进器产生的力、力矩来抵抗外界环境的力、力矩，使得船舶保持在所需求的位置以及艏向上。[1]

深水铺管船是当前海洋石油技术领域中非常重要的设备之一，担负着海底油气管道的铺设任务，其工作性能直接影响着石油产业的发展。要实现深水铺管船在环境多变海面上的船位和艏向的保持能力，动力定位系统必不可少，其利用自身推进器产生的推力，有效产生力矩和反力矩以抗衡外界力和力矩以保持船位。深水铺管船因作业要求而需要对船舶进行特种运动控制，而动力定位系统成为其特种运动控制不可缺少的支持系统，在这种的形势下，如熔盛重工建造的海洋石油201这类装配有动力定位系统的深水铺管船应运而生。本文根据深水铺管船动力定位系统的特殊性并结合其推进器配置方案，重点分析在此配置方案下的推力分配策略，采用SQP算法进行推力最优分配，通过Matlab仿真结果确立了具体推力分配的方案。

1 深水铺管船推力分配问题描述

推进器的推力分配策略是将控制系统发出的一系列变化的推力指令转换为时变控制信号给各个推进器，以此来产生相应推力的过程。推力分配逻辑的设计直接影响到推进器推力大小和方位角的输出，多推进器之间的推力分配问题实质上就是一个优化问题，要求推进器在每一个采样时刻都给出每个推进器所需要的推力，推进器系统整体性能要求的提高，以及新型推进器的引入都促进了推力分配逻辑的发展。深水铺管船动力定位系统依靠自身配备的7个全回转推进器为全船提供推力，以保持船舶的位置、艏向角与指令位置和艏向角一致，如图1所示。

推力分配模型的研究方法为假设铺管船推进系统配备n台全回转推进器，推进器i坐标位置为ri=[lx，i，ly，i]（在铺管船固定坐标系中相对于船体本身旋转中心的位置），每个推进器可以在角度θi的方向上产生大小为Fi的推力。因为全回转推进器在水平面上可以产生任意方向的力，可以将其分解在铺管船固定坐标系的两个方向上，即 u=[ui，x，ui，y]，其中 ui，x=Fx，ui，y=Fy是广义推力 u 在纵向和横向上的分量，广义推力 u 和推力指令τref存在线性关系，如式（1）、（2）所示。

图1 推进器布置示意图

目前关于动力定位系统推力分配问题的研究比较广泛，很多国内外专家与学者提出了推力分配的多种要求，当下已经形成系统的多目标优化问题，推力分配问题基本要求主要包括能耗最小化、保证动力定位的位置精度、避免推进器的推力峰值、艏向最优等。[2]

结合推力分配的目标，推力分配问题如式（3）所示。

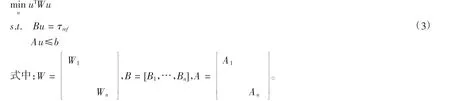
这是最简单形式的以最小化能量消耗的推力分配问题的描述，应用二次规划方法解决。其中需要解决的是每个推进器推力区域的非线性不等式Au≤b的约束问题，在此基础上为了最小化推力指令与推进器实际输出之间的推力误差，引入了松弛因子s，同时考虑避免推进器达到推力峰值，对推力分配的模型进行改进，如式（4）所示。

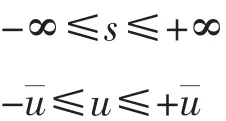
2 SQP算法基本原理

序列二次规划算法结合了线性搜索和信赖域方法，在求解小规模的非线性约束最优化问题上相对具有较大的优势，其工作原理是把最优化问题离散成一组等效的凸规划序列，形成序列间的迭代，从而求得最优解，如式（5）所示。

处理上述非线性规划问题时，其中目标函数f和所有的ci均为定义于Rn中的二阶连续可微函数，等式约束条件和不等式约束条件的下标集合分别记为E={1，2，…，me}，K={me+1，me+2，…，me}。在有约束最优化问题中，通常要将该问题转换为更简单的子问题，这些子问题可以求解并作为迭代过程的基础。

早期的方法通常是通过构造惩罚函数将有约束的最优化问题转换为无约束最优化问题进行求解，现在这些方法已经被更有效的基于K-T（Kuhn-Tucker）方程解的方法所取代，K-T方程是有约束最优化问题求解的必要条件。

因为f（x）、ci（x）、cj（x）二阶连续可为正则点，则存在拉格朗日乘子，如式（6）所示，这组条件就称为Kuhn-Tucker条件。

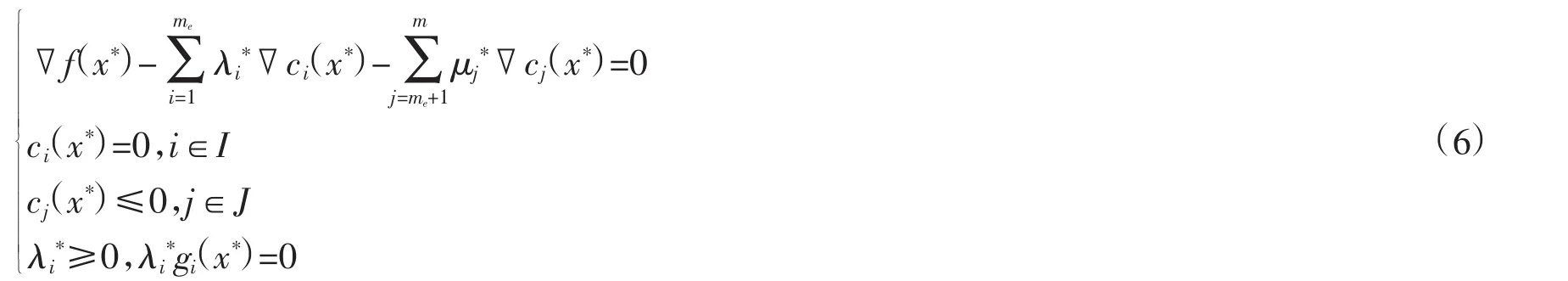
这个条件可以用来确定某个点是全局最优解，适用于有等式和不等式约束的NLP，其拉格朗日函数如式（7）所示。

式中：sk=xk-xk-1。

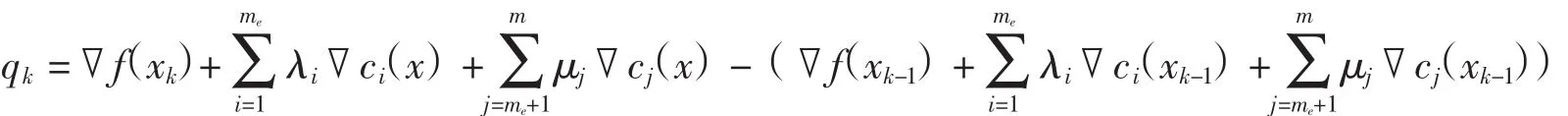
二次规划问题如式（9）所示。[3]

SQP法的基本迭代过程是：给定初值x0，B0，k=0；解二次规划子问题，确定搜索方向dk和λk+1；令xk+1=xk+dk，判断（xk+1，λk+1）是否满足收敛条件。若是，则令（x*，λ*）=（xk+1，λk+1），停止计算；否则令 k=k+1，返回上一步。

3 SQP算法数值算例与仿真

本文结合SQP算法考虑对象船舶推力分配的优化算例，在仿真程序中采用14×1数组代表所有的推力分配的输出值，包括每个推进器的推力大小和推力方位角的输出，转换成最优化问题，如式（10）所示。[4]

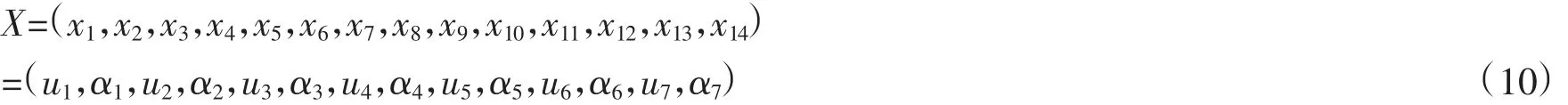
深水铺管船推力系统配备了7台全回转推进器，由于深水铺管船作业的特殊性，各推进器位置布置情况如1上表1所示。

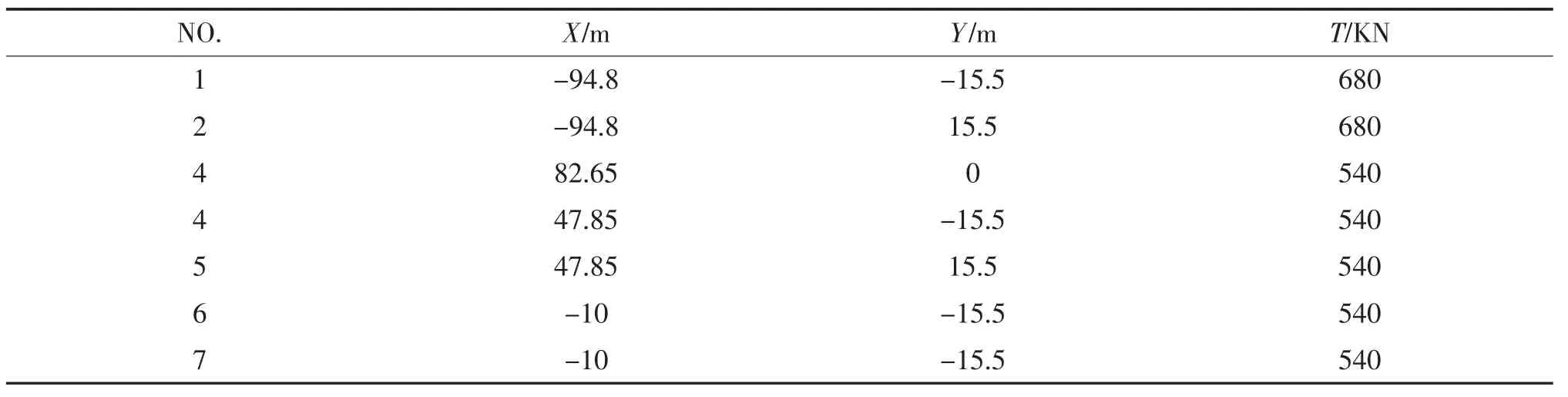
表1 推进器布置方案

模拟控制器的推力分配指令τref=[Fx，Fy，Mz]T作为推力分配模型的输入值，应用SQP算法得到输出值，即7个推进器的推力大小和推力方位角，图2为7#推进器的推力变及推力方位角随时间变化的曲线。仿真显示，作为主推进器的1#、2#推力值较大，其余推进器的最大推力峰值基本保持在600kN以下，且推力大小的变化表明在一定环境作用力下全船没有全方位控位能力，这主要是由于7#艏推所产生最大推力相对较小而导致。推进器方位角的变化则是由于对环境载荷模型简化及环境影响采用线性叠加引起的，故仿真结果会出现方位角的全回转过程，即1#、2#、5#、6#推进器的推力角度变化存在0°-360°/360°-0°陡转的情况。实际上铺管船在一定恶劣海况下是不允许出海作业的，外部严峻环境的影响会造成管道敷设过程中管子的拖曳及塑性变形等后果，所以对于恶劣环境载荷下的考虑并没有实际应用价值。

图2 7#推进器推力变化曲线与推力方位角变化曲线

同时，通过研究铺管船动力定位系统的推力分配策略，实现最小化能量消耗和推力误差，所以在仿真中模拟了控制器的推力指令，分别为水平方向上的力与艏摇力矩。图3所示为求解得到的各推进器推力产生的实际推力与模拟推力指令之间的比较，推力分配优化输出和控制器输入数值在纵荡、横荡方向基本吻合，在艏摇方向略微存在优化偏差，但总体上能够满足控制器的需求。本算例应用SQP算法求解推力分配的最优解过程中，每个推进器产生的推力视为一个有限区域的凸多边形，能够有效结合序列二次规划优化算法，使得推进器方位角变化更平缓，在一定程度上降低了能源损耗和减少推进器机械磨损，其对于推力分配策略选取来说是一种更加合理的选择，从而很好的满足了铺管船动力定位的要求。

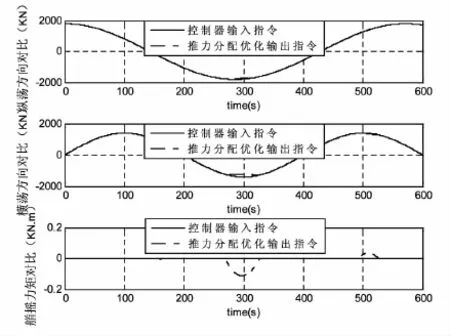
图3 推进器产生的实际推力与推力指令之间比较

4 结束语

本文应用SQP算法求解铺管船动力定位系统推力分配的最优解，给定了目标函数以及约束条件的确定方法。由本文的算例表明，SQP算法可以较好地满足深水铺管船动力定位的要求，对于提高动力定位系统的安全系数、可靠性以及控位能力具有重要作用，对于铺管船实际工程研究有一定的参考意义。

[1]童进军,何黎明,田作华,等.船舶动力定位系统的数学模型[J].船舶工程,2002(5):27-29.

[2]杨冰.实用最优化方法及计算机程序[M].哈尔滨:哈尔滨船舶工程学院出版社,1994.

[3]张申,王磊.动力定位推力系统研究[J].实验室研究与探索,2010(10):4-9.

[4]刘鹏.半潜式深海平台动力定位系统推力分配策略的研究[D].镇江：江苏科技大学,2012.