基于ESO算法的深孔机床多工况拓扑优化*
阴书玉 薄瑞峰 闫帅印 沈兴全
(①中北大学机械与动力工程学院,山西 太原030051;②山西省深孔加工工程技术研究中心,山西 太原030051)
床身是深孔机床的重要基础件,其自身质量和静动态性能对机床的加工精度和整机态性能均有较大影响。Z8016小直径深孔钻床床身的原始结构设计借鉴以往的设计经验,未充分考虑结构、材料的最优布局及床身的轻量化问题,导致结构粗大笨重,从而直接影响到机床的静动态特性及加工性能(深孔加工的直线度)。随着机床向高速化和精密化的发展,传统的经验类比设计方法已远远不能满足高性能和轻量化的设计要求。如何在满足动静态性能要求的前提下实现其轻量化设计,有着重要的研究意义和应用价值。拓扑优化技术提供了一种很好的解决方案。
国内游小红等人[1]利用ANSYS软件对T2120深孔钻镗床床身进行拓扑优化,优化后床身低阶固有频率有明显提高,并达到了减轻其质量的目的。郭媛美等人[2]利用尺寸优化及拓扑优化对外圆磨床床身结构进行设计,在保证机构具有足够强度和刚度的基础上,实现了磨床床身设计重量的大幅度下降。但是,以上采用的都是基于变密度法的单工况拓扑优化。相对而言,渐进结构优化(ESO)不仅仅可解决各类结构的尺寸优化,还可同时实现形状和拓扑优化,无论应力,位移/刚度优化,或振动频率,都可遵循ESO的统一原则和简单步骤进行[3-4]。渐进法在优化过程中,单元只会出现删除或者保留两种情况,并不会产生类似于变密度法的中间密度这种情况,可以有效提高优化质量,并且容易利用现有的有限元分析软件实现,具有很好的通用性。
因此,本文首先利用ANSYS的APDL语言进行二次开发,开发了基于应变能准则的多工况结构渐进优化算法,并将其应用于床身的拓扑优化,得到了其最优的材料分布,最终显著减轻了质量,实现了床身的轻量化设计。
1 基于ESO算法的优化数学模型
ESO算法的优化准则为:逐步去掉结构中的低效材料(单元),使所获得的拓扑结构具有更好的承载性能。本文以多工况下允许的最大应变能为约束条件,重量最小化为目标函数,其数学模型表示为:
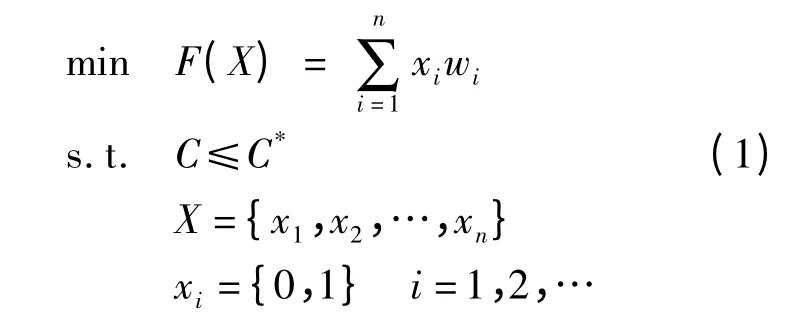
式中:目标函数F(X)表示结构总重量的最小化;设计变量xi表示第i个单元在模型中是保留还是删除,即取1或0两个值;wi为第i个单元的质量;C*表示允许的总体应变能的最大值,即结构总体刚度的最小值;n为单元个数。
结构柔度或者整体应变能的最小化等价于结构整体刚度最大化。
2 基于单元应变能密度的ESO法
2.1 单元应变能密度的公式推导
对于静力结构问题分析而言,相关的有限元公式如下:

式中:[K]是总刚度矩阵,{δ}是节点的位移矢量,{P}是节点的载荷矢量。结构的总应变能定义为:

从一个由n个有限单元构成的结构中删除第i个单元,总体刚度矩阵变化量为:
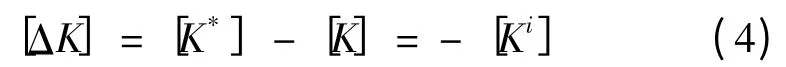
式中:[K*]是删除第i个单元后结构的总刚度矩阵,[Ki]是被删除的第i个单元的刚度矩阵。假设删除第i个单元不影响载荷矢量{P}。忽略高阶项的影响,从方程(2)得位移变化量为:

由式(3)、(4)、(5)可得:
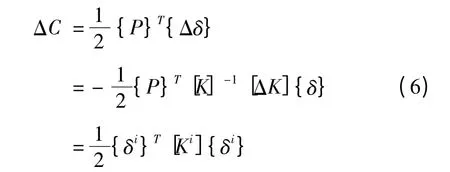
式(6)为由于删除第i个单元而引起的应变能的变化量,也就是单元应变能Ce,即

则单元应变能密度(灵敏度)为:

式中:vi为有限元单元的体积。
2.2 多载荷工况下的单元灵敏度公式
由式(8)可知多载荷下对应各个工况单元的灵敏度可表示为:

式中:{δik}是第k个工况单元的位移向量。
根据文献[5],可运用折衷规划法和功效函数法对多工况下单元灵敏度公式进行分析处理,即表示为:

上述对单元灵敏度公式的处理方法不仅能够使优化后的结构有效地减轻载荷“病态”现象,而且能够利用变化的权系数对优化过程进行动态调节。
2.3 多工况下的ESO优化算法步骤
对于各向同性线弹性材料静力结构优化而言,应变能优化准则的表达式可表示为:
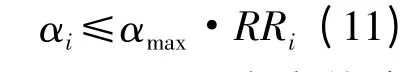
式中:αi是单元应变能密度(灵敏度);αmax是最大的单元应变能密度;RRi为删除率。
ESO算法原理简单,即通过将无效或低效的材料一步步去掉,使结构逐渐趋于优化。具体对于本文而言,ESO算法的思想是通过逐步删除单元应变能贡献最小的单元,使剩余结构的整体刚度逐步趋于最优化。
在ANSYS平台上实现ESO优化算法的流程图如图1所示。
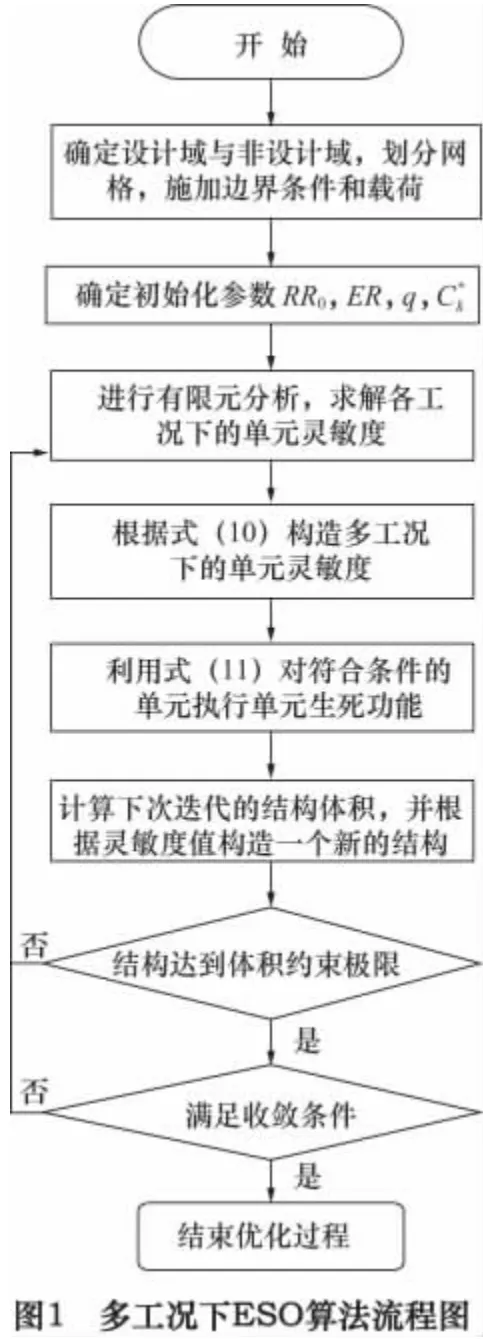
3 床身的拓扑优化
3.1 床身有限元模型的建立
Z8016深孔钻床床身为焊接件,床身长5 000 mm,宽416 mm,高870 mm,筋板厚度20 mm,前后壁厚27 mm,其内部筋板结构由7组V型结构的筋板组成。Z8016深孔机床如图2所示。

床身的材料为HT150,弹性模量为1.5×105MPa,泊松比为0.27,密度为7×10-6kg/mm3。采用Pro/E软件建立原床身三维实体模型,并将其导入ANSYS中进行计算分析。ANSYS采用智能网格划分技术对三维实体模型进行网格划分,单元类型采用soild92,得到148 943节点和75 504个单元。
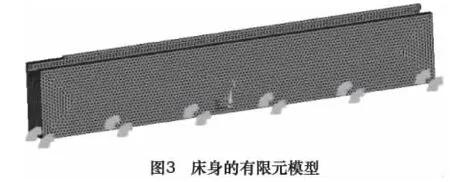
将床身的上面导轨部分和主轴箱支撑部分设为非设计区域,其他部分定为设计区域。ANSYS中设计区域划分的单元定为1号单元,非设计区域划分的单元定为相同材料属性的2号单元[6]。床身的有限元模型如图3所示。
3.2 床身的工况条件
床身的工况条件对于其结构拓扑优化设计的结果起着重要的作用。深孔钻床在切削加工时,主轴电动机功率、进给箱(尾座)相对于床身的位置、切削参数等主要因素影响切削工况。因此,综合上述的主要因素来确定床身的合理工况如下所述:
(1)极限工况 为确保床身具有良好的静动性能,选取深孔钻床重钻削时相应的极限工况为设计工况。
(2)进给箱位置的加权工况 进给箱相对床身位置的不同会导致床身的受力情况也有所不同。分别选取进给箱运行至床身的最小极限位置、中间位置和最大极限位置,并概率统计钻床的实际工作状态,通过引入加权系数来校正进给箱不同位置对床身载荷受力的影响。
综上所述,床身的典型设计工况为:钻床在重钻削条件下即主轴电动机满载功率时的切削力作为外部载荷;进给箱位于床身的最小极限位置、中间位置和最大极限位置作为3个典型工况。
3.3 床身的载荷和约束条件
床身3个典型工况的约束条件相同。即床身底部通过12个地脚螺栓跟地面连接,故在床身底部连接螺栓处定义全约束,各个方向的自由度为0。施加面约束后如图3所示。
床身所受载荷主要由两部分组成:重力和扭矩。即主轴箱、中心架、授油器、进给箱等的重力,以及由切削力转化而成的扭矩。将位于床身导轨上主要部件的重力等效为面载荷进行施加,由主要部件相应位置的平轨和V型轨上各平均承受总重力的一半[7];切削加工时,床身所受的扭矩同样等效为面载荷施加在支撑主轴箱和进给箱的导轨面上,施加载荷后如图4所示。

3.4 床身的ESO方法优化结果
选取基于应变能准则的单元初始删除率为RR0=1%,进化率为ER=1%[8],通过上述基于ESO法的多工况结构拓扑优化最终获得良好的拓扑优化图样,即删除率为RR=25%的结构稳定状态,如图5所示。

从图5所示可以看出,床身的材料主要集中分布在受力的导轨和工作台支撑部分的下侧以及进给箱(尾座)经常工作的床身区域部位。
为了更加形象地展示拓扑优化中床身的变化情况,因此绘出了床身的进化历程曲线,如图6所示。

从图6a可以看出:在删除率达到17%后体积减小的速度变缓慢;删除率从25%到27%的过程中,体积比基本不变,即也说明了拓扑形状不再发生变化;当删除率到达28%时,计算终止;最后拓扑结构体积为原体积的46%左右。
图6b中D表示3种工况中最大与最小应变能密度比值的平均值。从图6b中可以看出:lg(D)的值随着删除率的增加而逐渐降低到1.8,即最大与最小应变能密度比值逐渐减小到优化解时的101.8。这充分说明了最大与最小应变能密度的差距显著减小,床身取得了良好的优化效果。
4 床身的重构设计
根据拓扑优化结果即图5以及制造工艺,对原床身有以下改进措施:(1)在床身两侧壁上开孔[9]。(2)筋板上圆孔的直径由原来的100 mm变为200 mm。(3)下底板厚度由原来的25 mm变为18 mm并在其上开4个圆形孔,圆孔直径为350 mm。(4)合理地分配筋板数目,即减少床身前端部分的筋板数,增加支撑主轴箱部位的筋板数。经过反复的分析与验证确定新床身的结构如图7。

利用有限元法分别对原床身结构和优化后的结构进行静力学分析以及模态分析,优化前后床身的性能对比如表1所示。

表1 优化前后床身静动态性能和重量的比较
由表1所示:优化后床身的低阶固有频率有所提高,且远离工作频率,不会发生共振现象;最大变形量、最大等效应力都有所减小;最重要的是床身整体质量减小了14.47%。
5 结语
(1)借助ESO算法实现,利用APDL语言对ANSYS单元生死功能进行二次开发,实现了多工况下基于应变能准则的渐进结构优化算法。
(2)运用上述基于ESO法的多刚度拓扑优化算法,对深孔钻床床身进行了多工况下的结构拓扑优化设计,获得了良好的拓扑结构。在保证满足工作要求的前提下,其静、动态性能均有所提高,质量显著下降,节约了制造成本,实现了床身轻量化设计。
(3)本文的优化结果对床身的进一步尺寸优化和设计提供了参考模型,同时,该设计方法对机床其它部件的改进有一定的参考意义,有利于降低深孔机床的设计成本,具有较好的工程应用价值。
[1]游小红,薄瑞峰.深孔钻镗床床身的有限元分析及拓扑优化[J].组合机床与自动化加工技术,2013(1):96-98.
[2]郭媛美,郭春星,陈叶林.外圆磨床床身结构的拓扑优化设计[J].精密制造与自动化,2010(1):39-41.
[3]Chu D Nha.,Xie Y M,Hira A,et al.Evolutionary structural optimization for problems with stiffness constraints[J].Finite Elements in Analysis and Design,1996,21(4):239-51.
[4]Zuo Zhi Hao,Xie Yi Min,Huang Xiaodong.Evolutionary topology optimization of structures with multiple displacement and frequency constraints[J].Advances in Structural Engineering,2012,15(2):359-372.
[5]罗震,陈立平,张云清,等.多工况下连续体结构的多刚度拓扑优化设计和二重敏度过滤技术[J].固体力学学报,2005,26(1):29-36.
[6]张朝晖.ANSYS12.0结构分析工程应用实例解析[M].3版.北京:机械工业出版社,2010.
[7]段朋云,丁晓红.机床T型床身结构的筋板布置型式研究[J].机械设计,2013,30(5):71-74.
[8]范文杰,徐进永,张子达.基于双向渐进结构优化法的装载机动臂拓扑优化[J].农业机械学报,2006(11):30-33.
[9]倪晓宇,易红,汤文成.机床床身结构的有限元分析与优化[J].制造技术与机床,2005(2):47-50.

