液化天然气低温贮存分层研究

韩一飞

(西安航空学院 动力工程系，陕西 西安 710077)

1 引言

在低温液体停放和运输阶段中，液体内部会出现温度分层现象。研究分层现象下温度分布的方法有三种，即实验、理论和数值模拟。由于低温液体储罐内的温度不易测量，且实验方法获得的数据误差大，特别是在宇航领域，对于装有液氢、液氧的密闭燃料室，温度热分层现象更加不易测量。因此，合理建立模型，科学简化，通过理论分析计算储罐内温度分布解析解，带入具体工业实践参数，对结果进行分析并证实其有效性，从而为后续利用Fluent软件进行大量数值模拟提供参考对比的实际意义。

在以上认识的前提下，本文以100%纯甲烷为例，建立分层几何模型，列出数学模型，对模型简化求得纯甲烷在储罐内温度分布的理论解析解。并从工业实践中获得液化天然气储罐的具体尺寸参数和环境参数，带入解析解，从而计算储罐内不同高度下各点经过不同时刻温度值。最后，对计算结果进行分析，总结温度分布规律。结果表明，规律与已有大量文献研究结论吻合，该方法所得解析解是有价值的。

2 构建模型

2.1 原始数据

LNG容器：圆柱形竖放，内径10m，高12m；材料：不锈钢，外表珠光砂绝热20mm厚；常压；气体纯度：100%CH4。

2.2 理论基础

建立分层几何模型。为便于理解绘制了分层模型示意图，如图1所示：

图1 液化气分层模型示意图

(1)分层模型

本模型假设，靠近储罐壁面的液体首先受热自然对流上升，在液体上部形成温度分层区。分层区内的温度呈上高下低的幂次分布。由于热量随液体的流动不断传人，因此分层区不断加厚。为了求解分层区的形成过程，首先需要知道自然对流的发展。自然对流边界层的动量与能量方程如下。

动量方程：

(2-1)

能量方程：

(2-2)

将式(2-1)和式(2-2)的边界层温度和速度无量纲化，同时假设边界层厚度和特征速度的分布为δ=a1xm1，U=a2xn1。求解得到a1、a2、m1和n1，可以得出液体分层区厚度随时间的变化规律。同时，分层区的温度分布符合幂次分布E(Z)=mZn(m，n，为常数，Z为分层区底部以上的高度)。利用该式可以求出温度分布式为：

(2-3)

式中 A——受热面积；

δσ——分层区总高度；

Z——距离分层区内底部的高度；

t——加热时间。

从而可以计算得到储罐内相应的压力。

(2)LNG储罐周壁在环境漏热情况下的热流密度。

取环境温度20℃，即为293.5K，空气的对流换热系数为h0=7.6W/m2K，取珠光砂的导热系数为λ=0.05W/m·K。在0.1MPa的时候，纯甲烷的饱和温度t=111.51K。在0.6Mpa的时候，纯甲烷的饱和温度t=138.73K。在这一分层模型中，因为储罐内的对流换热系数较大，所以忽略其对流换热热阻，与此同时忽略不锈钢壁的导热热阻。

下式中，A0是圆柱体外径下的周壁面积，A是内径下的周壁面积。

所以传热量Φ=kA0(293.5-111.51)=qwA

=343.2174W/m2

3 温度分布计算及分析

本文对100%纯甲烷储罐内的温度分布的计算基于(2-3)式，在开始时刻，即在0.1Mpa时，整个储罐处于平衡均相状态，全场温度都对应0.1Mpa的饱和温度。根据圆柱储罐的对称性，我们可以得知圆柱储罐的中心轴线就是其内部温度分布的对称线。这一模型中，储罐壁面在漏热的情况下形成分层，随着储罐内液气分界面处液体的蒸发，其上部的气腔的压力会一直增大，直到增大至0.6Mpa。但是因为这是一非定常过程，即在这一时间段内，这一气腔内的压力值是一直在变化的，为了简化这一复杂模型。我们假设在一瞬间气腔内的压力达到0.6Mpa。这样储罐内的气液分界面处的温度瞬间达到138.73K，即0.6Mpa对应的饱和温度。此后热量不断向液相区底部渗入，随着时间的延续，直到最终整个储罐内达到新的平衡均相状态。在计算过程中，由于温度是一直在变化的，所以其物性参数也是一直在变化的。所以在公式(2-3)的应用过程中，通过软件可以获得100%天然气在任意温度、0.6Mpa定压下的ρ，c值，带入公式，便可以求出储罐不同高度，及经过不同时间后温度大小。

3.1 各高度下随时间变化温度的增加值

把经历不同时间长短后的温度增加值制作如表1，并画出相应的图形曲线，如图2所示。这一图示中横坐标表示经过一段时间后，储罐内部的某一高度下的温度值在0.1Mpa时最初均匀温度场111.51K的差值。

表1 纯甲烷情况下经过一段时间后液相区不同高度下温度增加值

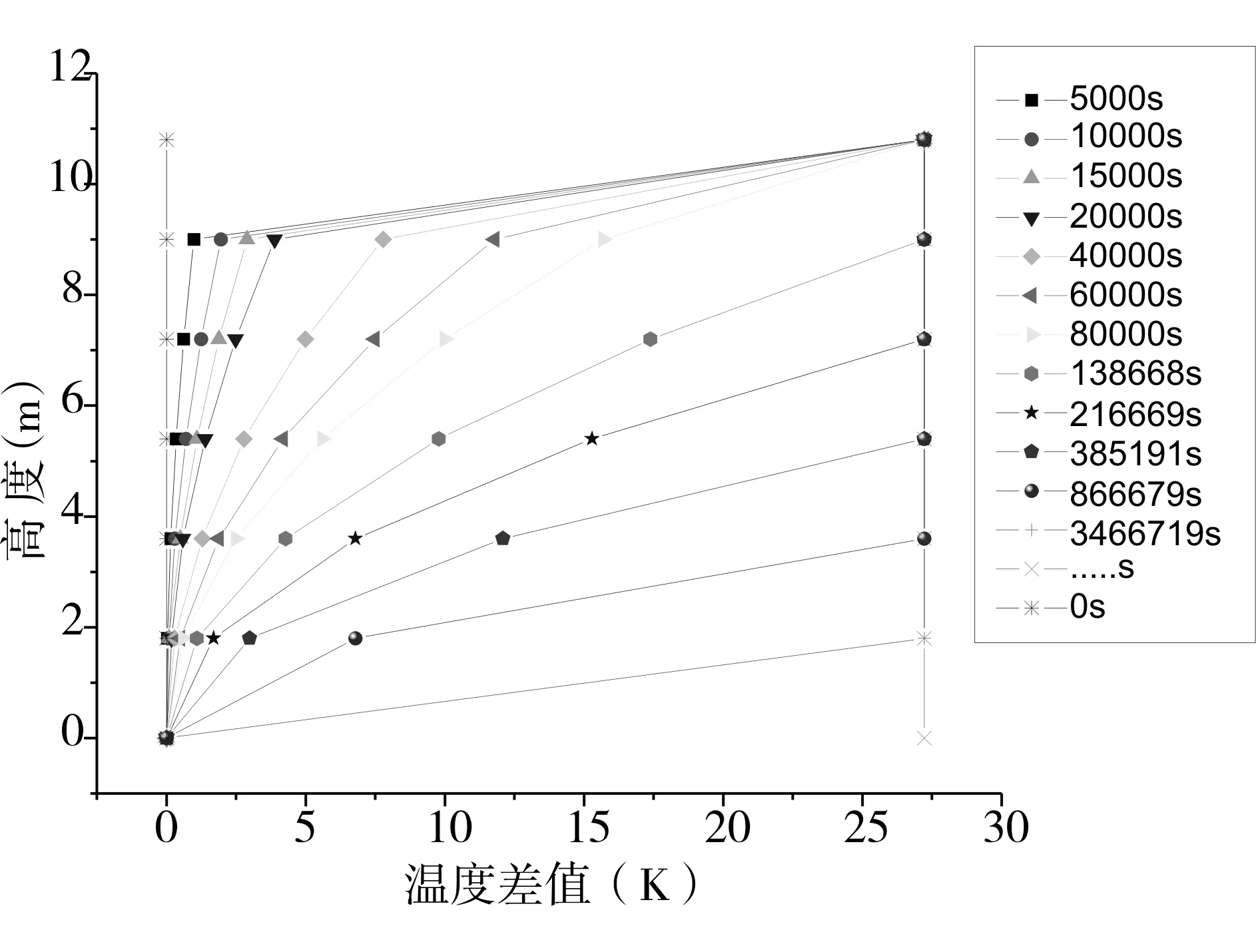
图2纯甲烷情况下经过一段时间后

液相区不同高度下温度增加值

随着时间的变化，气液分界面处的温度会一直保持不变，即138.73K，而其他较低高度下随着时间增大都会相继达到138.73K，当时间趋向无穷大的时候，整个温度场会变得均匀，即0.6Mpa对应的饱和温度。

3.2 经过特定时间，各高度下温度大小

在LNG的存储和运输过程中，由于分层现象的存在，从而使得在液相区的上部，其温度变化越快，热流更多的向上流动，进入储罐的能量更多的集中于液体上部的分层区，使温度呈现上高下低的特点。

由表2数据，绘制经过特定时间，各高度具体温度值的曲线。发现经相同时间后，液相区上部的温度值较大。随着时间的延续，液相区的温度值不断增大，最终保持138.73K不变。此后，液相区的上部的等高度下，其温度变化为0K，但下部等高度位置没有达到138.73K，温度随时间会继续增大直到138.73K。高度越高，其达到138.73K所用时间越短。温度变化规律如图3所示：

表2 液相区各高度下在经过10000s，20000s，40000，80000，138668s，385191s，3466719后的温度值后的温度值

图3经过特定时间，各高度温度值

3.3 经过不同时间，特定高度下温度大小

表3 在10.8m，9m，5.4m，1.8m下经过不同时间后的温度值

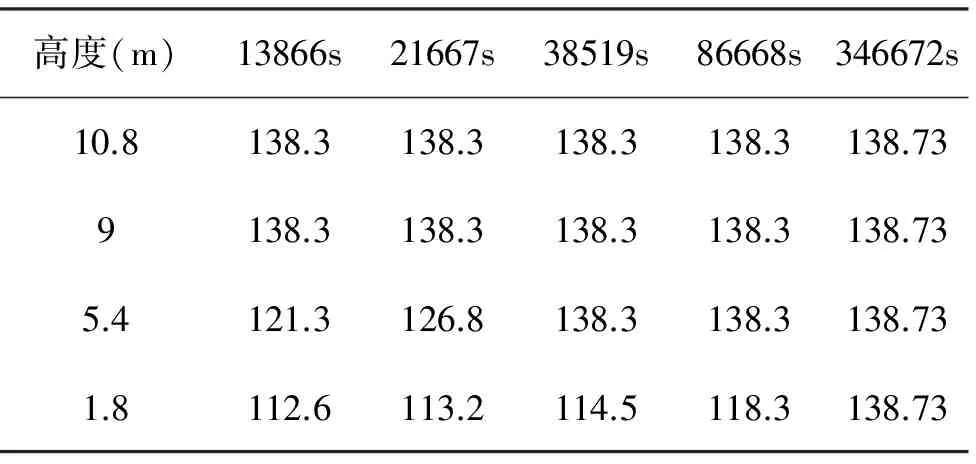
表3(续) 在10.8m，9m，5.4m，1.8m下经过不同时间后的温度值

由表3数据，绘制特定高度下，时间不断增大各高度具体温度值的曲线。发现高度越高，其越容易达到0.6Mpa对应饱和温度138.73K。曲线斜率随高度降低而不断减小，即高度越高，温度变化越快。温度变化规律见图4：

图4 经过不同时间，特定高度温度值

3.4 纯甲烷从整体初态0.1Mpa达到0.6Mpa所耗用时间

为了使得LNG储罐内顶部的气腔内的压力由0.1Mpa上升到0.6Mpa，那么就需要有5倍于上部气腔的气体质量汽化，即这产生的5倍汽化气体所吸收的热量全部来自液化天然气储罐漏热。同时在这一过程中，忽略液体减少而使气体体积的增大量。

下式中m初表示开始状态时气腔部分的质量。

在0.1Mpa时，汽化潜热 h=511.2KJ/Kg

ρ初=1.7946Kg/m3

在0.6Mpa时，汽化潜热 h=448.84KJ/Kg

所以根据：qwAt=5m初h

由于在这一加热过程中，温度是随时改变的，压力也是在0.1Mpa至0.6Mpa之间不断变化的，而汽化潜热值是压力的函数，因为我们不能得到单位时间步长下的压力变化范围，所以不能对汽化潜热值的值进行精确计算，这里，用0.1Mpa，0.6Mpa两个端点的汽化潜热的平均数作为这一过程中的恒定汽化潜热值。

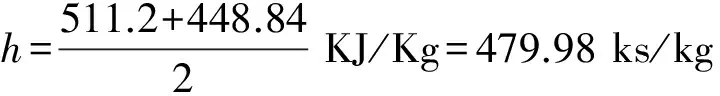
4 结语

通过计算结果分析，可以得出以下结论：

(1)随时间变化，气液分界面处的温度会一直保持不变，即为138.73K，而其他较低高度下随着时间增大都会相继达到138.73K，当时间大于0.968小时，整个温度场会变为均匀场，即都达到0.6Mpa对应的饱和状态。

(2)经过相同时间，液相区上部的温度值较大，热流更多的向上流动。同一时刻，储罐内温度呈上高下低的特点。

(3)不同高度下，液相区的温度值不断增大，最终都会到达并保持138.73K不变。我们发现高度越高，其达到0.6Mpa对应饱和温度的时间越短。

(4)经前文计算，我们得出储罐内汽相区压力由0.1Mpa达到0.6Mpa所需的时间是0.968小时。说明在储罐壁面漏热情况下，由于分层现象的存在，储罐内纯甲烷升温速度较快。

上述低温分层温度分布规律和已有大量文献研究结论吻合，该分层几何模型与数学模型基础上所得温度分布解析解是有价值的，起到为将来进行大量数值模拟提供参考对比的实际意义。

[1] 程栋，顾安忠.液化天然气的贮存分层现象[J].深冷技术，1997(1)：13-15.

[2] 李品友，顾安忠.液化天然气贮存非稳定性的理论研究[J].中国学术期刊文摘(科学快报)，1999，5(2)：170-172.

[3] 林文胜，顾安忠，李品友.液化天然气的分层与漩涡研究进展[J].真空与低温，2000，6(3)：125-132.

[4] 程向华，厉彦忠，陈二锋.火箭液氧贮箱热分层现象数值模拟[J].低温工程，2008，162(2)：10-13.

[5] 程向华，厉彦忠，陈二锋，等.新型运载火箭射前预冷液氧贮箱热分层的数值研究[J].陕西：西安交通大学学报，2008，42(9)：1132-1136.

[6] Cheng Xianghua，Li Yanzhong，Chen Erfeng， et al .Effect of return inlet on thermal stratification in a rocket tank[J].Journal of Thermo-physics and Heat Transfer，2010，24(1)：112-122.

[7] 程向华，厉彦忠.低温液体热分层特性分析[J].低温工程，2011,183(5)：50-55.

[8] 江帆，黄鹏.Fluent高级应用与实例分析 [M].北京：清华大学出版社，2008(7),73-138.

[9] 张凯，王瑞金，王刚.Fluent技术基础与应用实例 [M].北京：清华大学出版社，2010.9,125-137.

[10] 游立新，顾安忠.液化天然气的分层和漩涡及防止措施[J].石油与天然气化工，1991,20(3)：21-25.

[11] 李品友，顾安忠.LNG涡旋及预防措施[J].低温与特气，1998,(2):54-57.

[12] 李品友，顾安忠.液化天然气涡旋的理论研究[C]. 水动力学研究与进展(A辑)， 2000，15(2)：182-190.