等待期权对数字保存项目投资评价的影响——基于用户访问价格的离散变化分析

杨敏

（中山大学资讯管理学院，广州 510006）

等待期权对数字保存项目投资评价的影响
——基于用户访问价格的离散变化分析

杨敏

（中山大学资讯管理学院，广州 510006）

计算项目投资收益的净现值（NPV）可以评价投资产生的经济效益。由于数字保存项目的投资过程存在着许多不确定因素，在不同时间进行的投资可能会产生不同的收益净现值，所以数字保存项目的价值受等待期权价值的影响。文章引入等待期权定价理论，分析影响用户访问价格的因素，进而采用模型分析法，分别建立了基于用户访问价格的二阶段和三阶段离散变化模型案例，量化了等待期权的价值，给出了最优投资决策，说明了用户访问价格对项目投资评价的重要影响。

等待期权；数字保存项目；投资评价

数字保存是指对数字资源进行长期维护的一项活动，其目的在于确保数字资源的可用性、真实性与完整性，从而向用户提供可信任的数字资源访问服务。其兼顾有资源价值、社会价值。基于市场机制运营的数字保存项目可以看作一种经济类的商品，具有商品的经济因素，主要包含其隶属于经济产品的归类（公有、私有），影响产品供给与需求的特性。

1 选题缘起

1.1 等待期权定价理论

从经济学角度来说，项目建设存在着一个投资时机的选择问题。根据传统经济学理论，投资时机的选择依据的是项目的收益现值与直接成本的比较，当前者大于后者时，投资可行；否则，投资不可行。例如一个一年期项目，成本150万元，收益180万元，当年的无风险利率是10%，那么：收益现值-成本=180÷ (1+10%)-150=13.6(万元)＞0，因此当年投资可行。但是，采用这种方法进行投资决策是欠科学的，因为在投资时机延迟后，项目收益会附加上期权的价值，比如，针对上述项目，假如次年的无风险利率是7%，如果次年投资，那么：收益现值-成本=[180÷(1+7%)-150]÷ (1+10%)=16.6(万元)，很明显，次年投资比当年投资收益更大，次年作为投资时机更佳。因此，在有些情况下，延迟投资是有价值的。

对可以延迟投资的项目通过传统净现值法和期权方法计算出的投资结果的差异，源于项目投资的灵活和风险特性带来的等待期权的价值，所以上述项目的总价值计算方法应该为：项目总价值=净现值（NPV）+等待期权的权值。

传统研究项目投资机会和投资决策的方法是建立等待期权的离散时间模型，而二项式法广泛应用于使用动态规划思想求解离散型等待期权的计算过程，其思路是以某一定比例n建立无风险投资组合，若该组合在短期内收益率可以假设等于无风险利率，那么组合中的参数需要规划与整合。通过确定投资组合的总价值，那么按无风险利率贴现到当前的值就可求出该组合的投资成本，最终明确期权的价值。需要注意的是，在各时间区间中，标的资产有两种变化可能（上或下），但变化的结果只能取其中一个，就像是树上的两个分叉。对于多数投资项目而言，投资机会不会瞬间消失，这种机会对决策者是一种权利，在不同的时间节点可以选择立即执行期权也可以放弃期权执行，见图1。

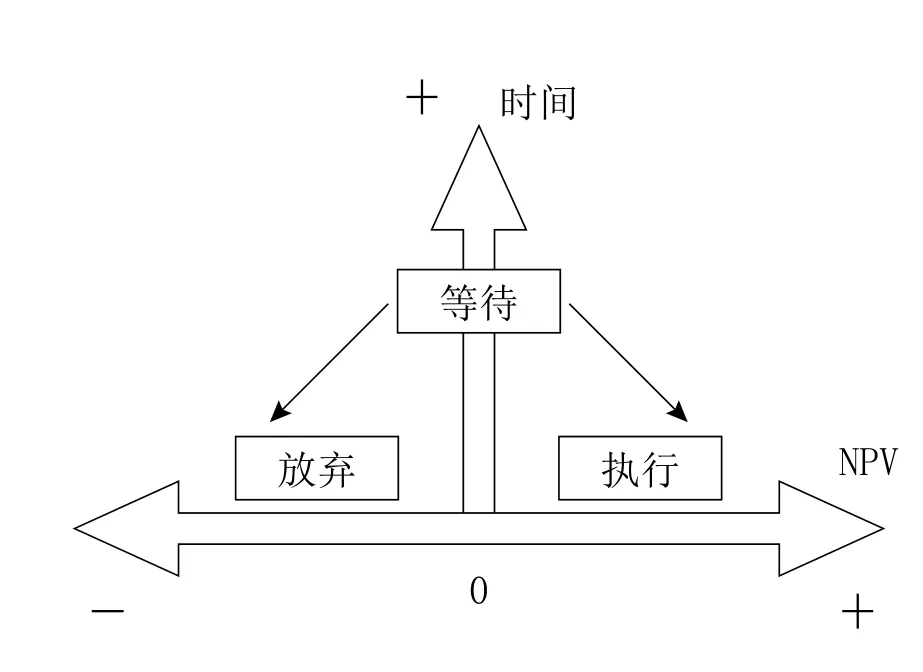
图1 等待期权的三种投资决策

1.2 数字保存项目内涵的等待期权

数字保存项目投资的不确定性包含利益和损失双重因素，利益是不确定性中有利的因素，不利的因素就是损失，项目投资包含的有利因素可以给投资者带来额外的价值，而等待期权方法考虑了项目的有利因素带来的价值，特别是期权价值。等待期权理论认为有利条件发生的不确定性越大，期权价值就越大，项目总价值也越大。虽然数字保存项目投资受到数字保存技术、报错规模、市场政策等不确定条件的影响，不过由于人们使用数字资源参考学习意识会逐步提升，对数字保存方法的倚重，国家对数字保存项目投资的政策支持，如果以这种势头发展，这种不确定性有利于保存项目投资的不确定因素。在评估这种不确定性强的项目的价值时，不确定性中有利因素（不利因素）带来的价值是不容忽略的，假如决策者决策时不考虑这部分将会错判项目投资的真正价值。把等待期权方法引入到数字保存项目投资开发中，就能够将投资中出现的不确定因素转化为投资决策的优势，提升投资选择空间，扩展投资机会，提高决策者投资的抗风险能力和投资决策水平。本文研究的数字保存项目重点考虑执行期权的可能性，即立即投资、推迟投资或放弃投资的选择权。

1.3 概念例子

由于本文研究的是基于市场机制运营的数字保存项目，项目的收益依靠的是有访问项目需求的用户量和用户访问项目需要支付的成本，即访问价格，这里重点研究用户访问价格对项目投资时机的影响。

假设一个数字保存项目拥有两段式投资时机选择：第0年和第1年，假设建设该项目需投资1800个单位货币，每年授权访问用户的数量为200个单位，在第0年每单位用户的授权访问费为每年1个单位货币，第1年访问价格增加到1.5个单位货币的概率为50%，降低到0.5个单位货币的概率也为50%，然后每个用户的授权访问价格就永远保持在这一新水平上，并假设无风险利率为10%。该项目在第0年投资的净现值为：

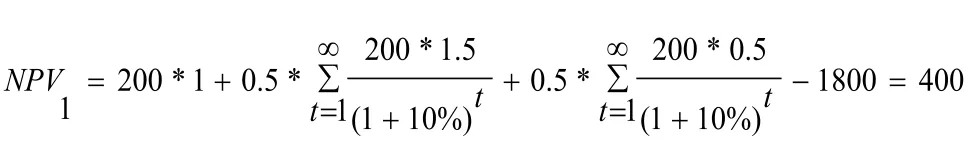
因为净现值为400＞0，根据传统的经济学理论，该项目在第0年投资可行。但是，这个结论是不正确的。为了说明这个问题，现在假设第0年不投资，等到第1年用户数量增加时再投资，那么，从第0年角度，该投资方案的净现值（贴现到第0年）为：

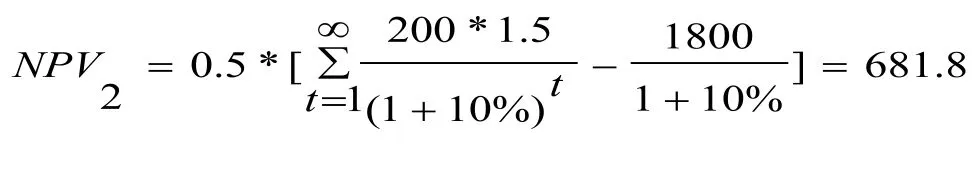
很容易发现，NPV2＞NPV1，等待比立即投资更好。在上述简单的例子中，在第1年，如果用户访问价格增加到1.5个单位货币，通过支付1800个货币单位来执行期权，获得价值为的资产，如果用户访问价格下降到0.5个单位，投资价值仅为1000个货币单位。显然，在考虑期权价值因素后决策者不会进行投资。

2 数字保存项目中影响访问价格的因素

在数字保存项目中影响授权用户访问价格的因素有很多种，总结起来有：

（1）保存技术。数字保存项目的建设和运营需要一系列技术支撑，这些技术既有移植来的，也有专用的，并且都与硬件或软件设备有关。移植来的技术是指将其他领域中使用的技术应用在数字保存项目中，如计算机与网络技术、数字扫描与拍照技术、数据传输与通讯技术、海量数据存储与分布式存储技术、OCR识别技术、数据安全技术等。专用技术是指针对数字保存项目开发的技术，如数字迁移与数字仿真技术，元数据析出技术，SIP（提交信息包）、AIP（保存信息包）、DIP（分发信息包）的生成、传输、校验技术，数字资源的检索与显示技术、数字资源质量检测与保障技术等。移植技术的成熟程度、稳定水平、购置费用和服务能力，以及专用技术的开发水平、开发成本等诸多因素都存在不确定性，并且都会随着时间的推移发生变化。

（2）数字资源产权状态。获得数字资源的产权许可是数字保存项目需要支付的不菲成本，但这项开支和数字资源的产权保护期限都在变化中。

（3）数字保存政策。数字保存是一类新型项目，相关政策逐步出台与完善，政策的不确定性也会影响数字保存项目的投资时机。

（4）市场供需关系。因为数字保存资源是一种市场产品，价格必然会受到市场供求关系的影响。一般来说，商品供不应求→商品短缺→买者竞争→商品价格高，商品供过于求→商品过剩→卖者竞争→商品价格降低，加上市场竞争的影响，买卖双方对利益的追逐成为了权衡数字资源访问价格的重要因素。

此外，用户的消费意识、数字资源的购买价格等也不同程度决定着用户的访问价格。上述影响数字保存项目访问价格的因素往往是随时间节点连续变化的，本文仅研究基于时间离散变化的价格变量，最终依据离散变化的访问价格变量建立两段式、三段式的投资模型。

3 投资模型建立

根据等待期权定价理论，假设一个数字保存项目，投资成本为C，每年用户访问量为M，用户初始访问价格为S0。贴现率为ρ，保持C、M、ρ三个参数不变，S0按照一定规律变化。

3.1 两段式投资模型

改变每年每位用户授权访问价格S，假设：

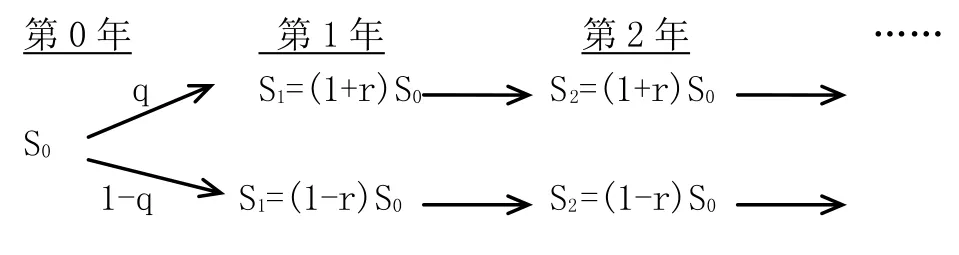
为了再模拟一个最优的投资决策，假设在第1年投资项目的价值为，当然，V1＞C时才会投资，即投资收益P1=max[0,V1-C]，假定S0位于价格在下一年上升到值得投资和下降到不值得投资的范围内。

（1）假定用户访问价格S0在第1年上涨，由前可知，如果此时V1仍小于成本C，则投资不可行，这种情况下计算

（2）S0为何值时，应当现在投资而不是等待呢？找到投资期权的价值就找到了临界价格。通过计算在第0年投资的项目净现值，并令它等于到第1年才投资时项目的净现值。然后以价格为基础决定是否投资。

如果数字保存项目的利润超过其等待的价值，即P0=V0-C≥E0(F1)，表示等待的成本（第0年利润的不足）超过了收益。测算S的临界值，由

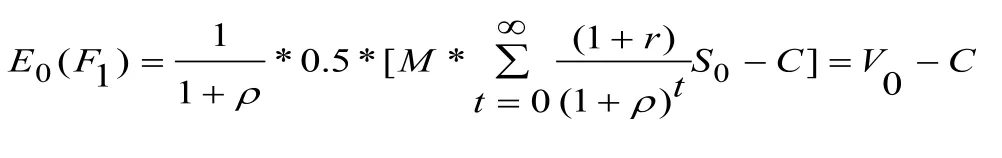
这样，项目的期权价值就是当前价格S0的分段线性函数，最优投资决策取决于S0。

如果，P0=0，人们永远不会对该项目投资；

如果则P0=E0(F1)，人们将等待一年再投资；

选择投资时间的基本思路是数字保存项目利润P0的最大化，即

假设访问价格S0是变量，P0是S0的函数，如图2很容易根据两条直线求出Sa和Sb。

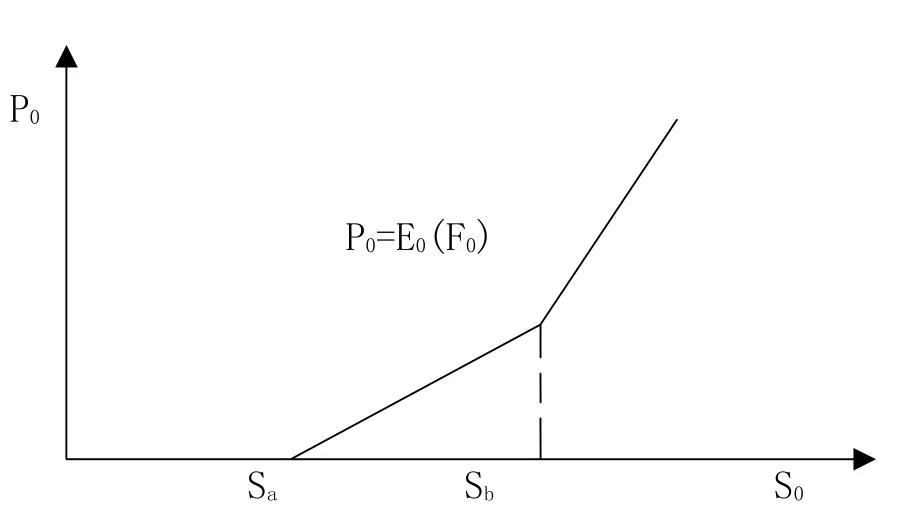
图2 授权访问价格对利润的影响

根据图2，可以看到P0是S0凸函数，并且P0大于等于现在就投资的净回报V0-C时，S0超过了最优执行点（Sb）。可以设计出最优投资时间（见表1）。

表1 访问价格决定投资时间（两段式）

3.2 三段式投资模型

同两段式分析模型一样，保持用户数量、投资成本、利率不变，项目投资时机有三个时间节点：第0年、第1年和第2年。

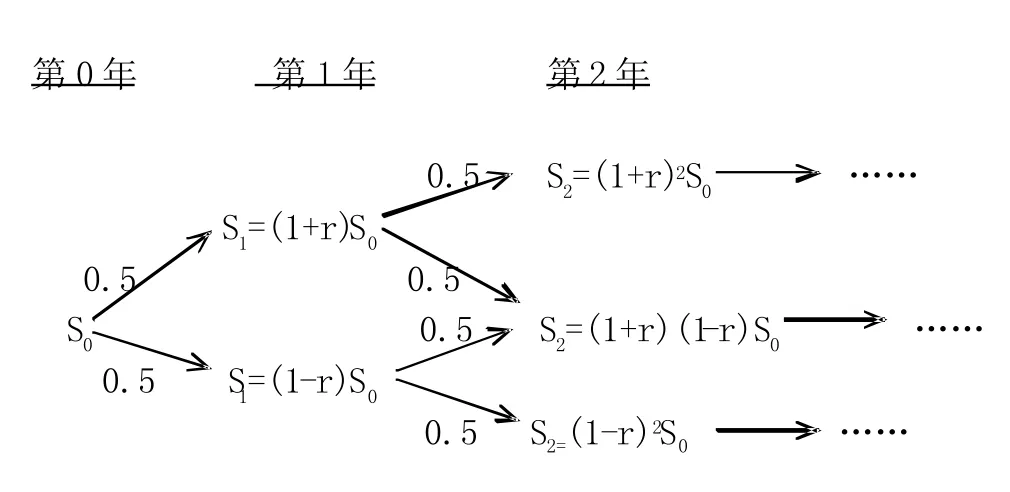
图3 访问价格三段式变化示意图

投资策略变为了5项：

A. 永不投资；

B. 等到第2年，只有价格在前两年都上升时才投资；

C. 在第1年，如果访问价格提高就投资，如果降低就永不投资；

D. 在第1年，如果价格提高就投资，如果价格降低，则等到第2年，若价格改为提高再投资；

E. 立即投资。

这就要求必须计算出每种情况下的期权价值。另外，通过构造一个无风险的投资组合来解决问题，但是这个组合在两年间并不是不变的，在第一年访问价格变化后，还需要改变组合内的价格保证，投资是无风险的。

为了得到最优的投资决策，需要第0年包含未知量S0的投资期权价值F0，同两段式一样，在第1年用户数量不定的情况下（S1=(1±r)S0），假定两种条件下暂时还未投资，通过在不同条件下构造无风险的投资组合计算收益情况，计算出在第1年投资期权价值F1，进而回到第0年，构造无风险的投资组合计算其收益来确定F0。

如果在第1年，S1=(1-r)S0，假定用户量S1处在这样的临界状态：如果用户量增长，在第2年就投资；用户量下降，则永不投资。现在构造一个无风险的组合包括投资期权和虚拟的一定数量的访问用户φ1S1，这个投资组合的价值为λ1=F1-φ1MS1。如果用户数量在第二年上升到（1-r2）S0，投资可行，，如果访问价格在第二年下降到（1-r）2S0，决策者不会投资，F2=0，λ2=-（1-r）2MS0φ1，令两种情况下的λ2相等，可以得出，如果，投资组合将是无风险的，无论访问价格上升还是下降，令投资组合的收益等于无风险投资收益，即λ2-λ1-ρφ*MS1=ρλ1。这里省略繁琐的计算过程，得到投资期权的价值。由上式可以看到，当时，F1=0，如果S0继续变小，则该项目的实际价值将小于投资成本。因此，如果访问价格在第1年下降，且，将永不投资。

相反地，假定访问价格S0在第一年增长到（1+r）S0，重复前面无风险投资组合的计算过程：如果价格增长，在第2年就投资；价格下降，则永不投资。得到无风险投资组合要求 ，进而计算投资期权的价值为。在这种情况下，当时，F1=0。由此，如果，将永不会投资，即便第1、2年访问价格都增长。此外，假定在第1年价格增长就投资，而不是等到第2年，这时项目的净现值。令右侧相等，计算初始用户数量的取值，可知当时，且在第1年访问价格已经上升，将在第1年投资，而不是继续等待。

以上已经知道了F1以及当S1在两种可能取值下的最优投资决策（此时还没有投资），进而可以再一次构造无风险的投资组合并计算其收益来确定F0，这里不再一一列举。

因为最优投资决策取决于S0，所以必须对不同范围的S0进行计算来辅助做出决策，沿用前面讨论过的两阶段的投资情况，即对

如果整个投资都是最优化安排，那么，该项目的投资净利润（贴现到第0年）为：

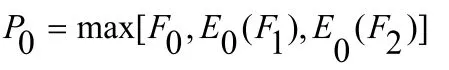
很明显，延迟期权是最优化投资的净利润与仅限在第0年投资的净利润之差，即：

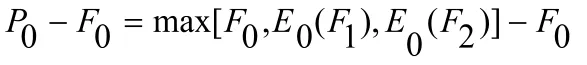
如果数字保存项目在第0年投资，不存在等待期权。只有在第1年或第2年投资，才有等待期权。

投资规则：与两段式一样，三段式投资规则构建的基本思路也是数字保存项目投资的净利润（即上述中的P0）最大化。很明显，P0是S0的函数。

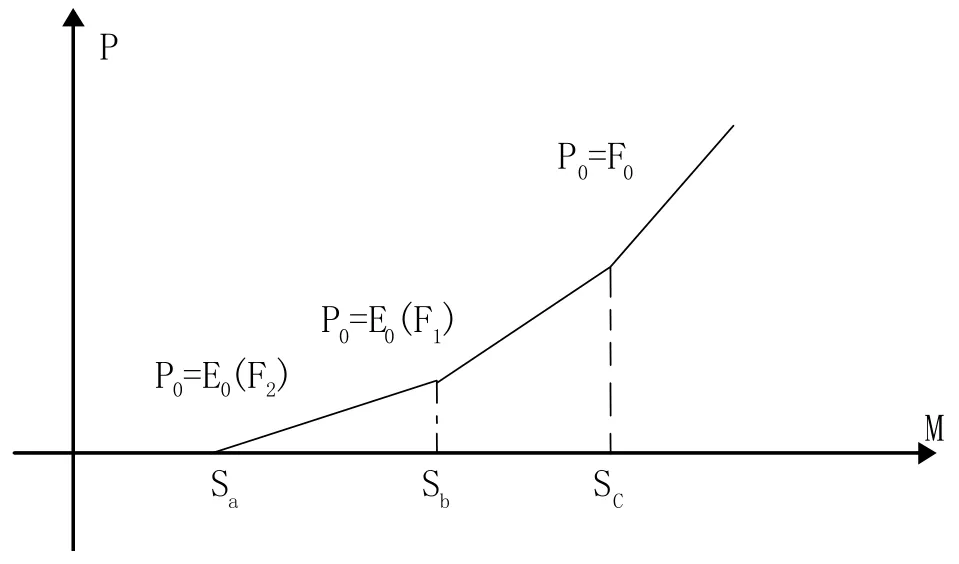
图4 价格变化三段式投资曲线

最优投资规则的曲线如图4。

图4中的Sa、Sb和Sc很容易根据三条直线方程求得。由此可以得出最优投资规则如下表4.2。

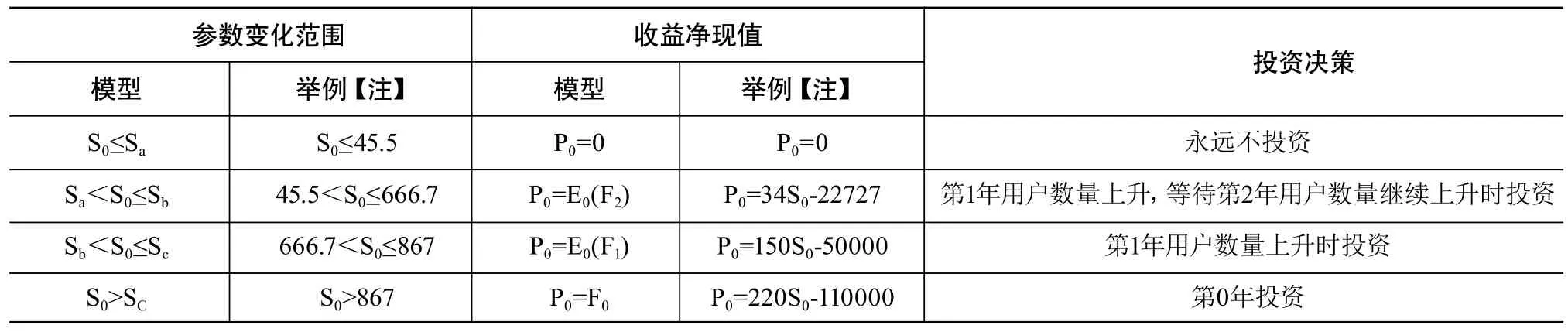
表2 价格变化三段式投资规则

4 结语

通过前面内容的介绍可以了解，数字保存项目投资较一般的投资项目而言具有不确定性大、持续性强等特点。由于净现值法没有考虑到不确定性给项目带来的价值、仅将投资者的选择权局限在要么立马投资要么放弃投资范围内，低估了项目的价值，造成投资该类项目无利可图的假象，再加上数字保存项目投资具有兼顾社会效益和经济效益、投资主体并不一定是收益主体的特点，许多投资单位和个人认为进行保存项目投资得不偿失，最终造成我国数字保存投资总量不足、投资主体缺失的现状。等待期权法考虑了数字保存投资项目不确定性给项目带来的价值，这类项目投资外部性对项目价值的影响将投资选择权扩展到立即投资、推迟投资、放弃投资这三项决策，科学、准确地估计数字保存投资的项目价值，能提高投资者对这类投资项目的积极性。

本文通过研究用户访问价格的离散变化对数字保存项目收益的影响，分别基于两段式和三段式的投资假设，提出了数字保存项目在不同时机投资的收益模型，总结出最优的投资决策。从图2和图4的模型中可以看出，收益是授权访问价格的凸函数，说明了在不同投资环境下，比如投资时段的增加将会降低“永不投资”的授权访问用户价格（表1中的两段式是333，表2中的三段式是45.5），这一数据从另一角度表明在非最优时机下进行投资会造成较大的损失，比如在净现值为零的情况下进行投资（见表1）。总的来说，数字保存项目延迟投资时段越多，投资时机的灵活性就越大，产生最佳收益的概率越高，数字保存项目的盈利能力越强。

本文的主要局限是只讨论了离散状态的投资时机，在实际应用中数字保存项目的投资时机可能更多的是连续状态，这是未来研究的方向之一，基本思路是借鉴著名的维纳过程（Wiener processes）和伊藤过程（Ito processes）对连续时间的处理方法，结合数字保存项目实例进行讨论、分析。

[1]BRENNAN M, SCHWARTZ E. Real options and investment under uncertainty: classical readings and recent contributions [J]. The MIT Press, 2000: 521-540.

[2]TRIGEORGIS L. Real Option and Financial Decision-making Contemporary Finance Digest [R]. MIT Press, 2000.

[3]LAVOIE B F. The Incentives to Preserve Digital Materials: Roles, Scenarios and Economic Decision Making [R]. OCLC Research, 2003.

[4]百度百科.增长期权[EB/OL]. [2014-11-20]. http://baike.so.com/ doc/3791499.html.

[5]豆丁网.财政金融-延迟投资的期权决策方法与应用研究[EB/OL]. [2014-11-20]. http://www.docin.com/p-167963723.html.

[6]臧国全,孙圣强,杨敏.数字保存项目的投资时机研究[J].情报科学, 2013,31(1):9-13.

[7]臧国全,安明,杨敏.基于延迟期权的数字保存项目投资规则建立[J].图书馆理论与实践,2012,31(7):27-30.

[8]王潇耿.基于成长期权的企业R&D投资时机研究[D].甘肃:兰州大学,2010.

[9]刘耀芳.实物期权理论在水利建设项目投资决策中的应用[D].西安:西安理工大学,2006.

[10]艾小莲.实物期权定价模型在房地产投资决策中的应用研究[D].江苏:江苏大学,2009.

[11]刘奕均.不确定条件下实物期权在投资决策中的应用探析[D].江西:江西财经大学,2006.

[12]臧国全,焦克非,王志辉.论数字保存[J].现代情报,2007,27(8):50-52.

The Influence of Waiting Option on Investment Evaluation for Digital Preservation Based on Discrete Changes in User Access Prices

YANG Min
(School of Information Management, Sun Yat-Sen University, Guangzhou 510006, China)

Calculating the project investment income net present value (NPV) can evaluate the economic benefits generated by the investment. The investment process of digital preservation projects has many uncertainties. Different times may produce different benefits of NPV. So the values of digital preservation projects are subject to the value of waiting option influence. This paper describes the waiting option pricing theory, and analyzes the factor of user access prices. then using the model analysis, based on two-stage change and three-stage user access prices, the discrete change model case are established. This quantized the value of waiting option, shows the optimal investment decision case, and explains important impact user access prices on the project investment evaluation.

Waiting option; Digital preservation project; Investment evaluation

G250.7

10.3772/j.issn.1673—2286.2014.12.009

2014-12-02）

杨敏，女，1988年生，中山大学资讯管理学院博士生，研究方向：数字图书馆，E-mail：olivemin@163.com。