一个判别函数一致连续性的新标准

周骁

（湖北汽车工业学院理学院，湖北十堰442002）

一个判别函数一致连续性的新标准

周骁

（湖北汽车工业学院理学院，湖北十堰442002）

借助于次可加的单调不减连续函数，给出了判别函数一致连续性的一个新的标准。

连续模函数;一致连续;次可加;单调不减

函数一致连续性的探讨是数学分析课程［1-2］的重要学习内容之一，也是学生学习较为困难的部分，因此有必要探究证明函数一致连续的方法。如文献［3］利用导函数及Lipschitz条件来得到判断函数是否一致连续的方法；文献［4］总结了一些证明函数一致连续的常用结论，并给出了证明方法的流程图。本文中将利用连续模函数来给出判断定义域为R的函数是否一致连续的一个新方法。

定义1［1］设f是定义在区间I上的函数。若对任给的ε＞0，存在δ=δ(ε)＞0，使得对任何

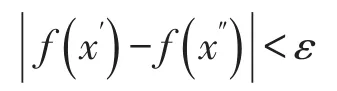
则称函数f在区间I上一致连续。

定理1f(x)在R上一致连续的充要条件为存在一个次可加的单调不减连续函数φ(x):R+↦R+且φ(0)=0，使得

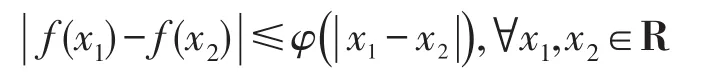
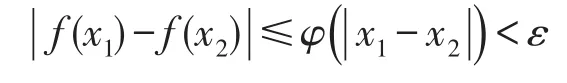
故f(x)在R上一致连续。

Step1 验证φ(r)被很好地定义。设任意x1,x2∈R且|x1-x2|≤r。因为f(x)在R上一致连续，所以对任意ε＞0，存在δ＞0，任意x,y∈R，只要进而存在n∈N+满足

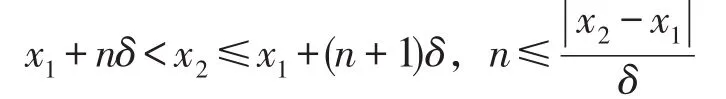
使得对任意x1,x2∈R有

［1］华东师范大学数学系.数学分析（上册）［M］.3版.北京：高等教育出版社，2001：79-82.

［2］ Rudin W.Principles of Mathematical Analysis［M］. Third Edition.Beijing:China Machine Press,2004:90-92.

［3］唐美燕.证明函数一致连续的几种方法［J］.贵州师范学院学报,2010,26（12）:7-10.

［4］钱伟懿.函数一致连续证明方法研究［J］.渤海大学学报：自然科学版，2011,32（4）:295-298.

A New Criterion for Uniform Continuity of Function

Zhou Xiao
（School of Science,Hubei University of Automotive Technology,Shiyan 442002,China）

A new criterion for uniform continuity of function was given by means of subadditive and monotone non-decreasing continuous function.

continuous modulus function;uniform continuity;subadditive;monotone non-decreasing

O177.2

A

1008-5483（2014）04-0051-02

2014-09-26

周骁（1986-），男，山东聊城人，硕士，从事偏微分方程的研究。

10.3969∕j.issn.1008-5483.2014.04.012