一致L-Lipschitz映象对公共不动点的迭代逼近

李万继

（湖北汽车工业学院 理学院，湖北 十堰 442002）

一致L-Lipschitz映象对公共不动点的迭代逼近

李万继

（湖北汽车工业学院 理学院，湖北 十堰 442002）

Banach空间中非线性算子的不动点的迭代逼近问题是非线性逼近理论中所研究的最重要的问题之一。通常用Mann和Ishikawa迭代法去逼近非线性算子的不动点。本文研究了Banach空间中一致L-Lipschitz映象对公共不动点的迭代逼近问题，改进和推广了文献［5－6］的相应结果。

渐近非扩张映象；渐近伪压缩映象；Ishikawa迭代序列；不动点

渐近非扩张映象和渐近伪压缩映象分别由Goebel-kirk［1］和 Schu［2］引入，它们密切相关于Banach空间中的不动点理论。关于渐近非扩张和渐近伪压缩映象不动点的迭代逼近问题在Hilbert空间或一致凸Banach空间的框架下被研究过［1－6］。2004年，陈与姚［5］研究了一致φ-伪压缩映象不动点的迭代收敛问题，这个定理改进和推广了许多熟知的结果。近几年，陈与姚［6］在上述定理基础上讨论了当T是具实数列｛rn｝的一致L-Lipschitz渐近伪压缩映象的情况下Ishikawa迭代序列强收敛于某个不动点。

笔者将继续此方面的工作，其结果在下列方面改进，推广和发展了先前熟知的结果：

1）将单个一致L-Lipschitz映象推广到一致LLipschitz映象对，因此改进和推广了文献［5-6］的主要结果。

2）修改了先前定义的Ishikawa迭代序列，并研究了迭代序列及其收敛性。

引理1［7］设X是实Banach空间，J∶X→2X*是正规对偶映象，则∀x，y∈X有

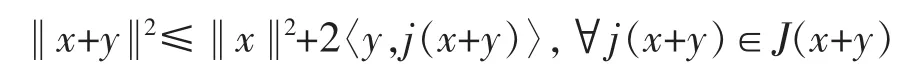
引理 2［8］设是3个非负实数列，且满足不等式

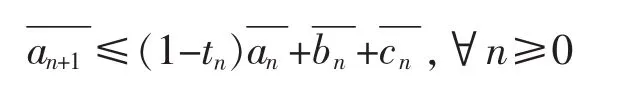
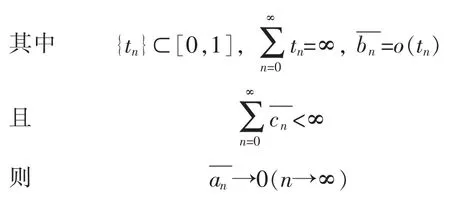
定理 设E是实Banach空间X的非空闭凸子集，T∶E→E是具实数列的一致 L-Lipschitz渐近伪压缩映象，L≥1且 S∶E→E是一致L-Lipschitz映象。如果

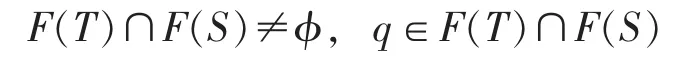
而且存在一严格增的函数

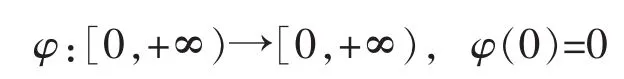
使得∀x∈E有

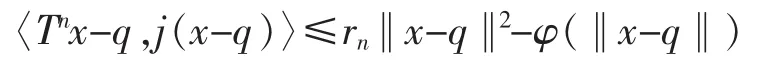
其中j（x-q）∈J（x-q）是按渐近伪压缩映象定义中由x和q所确定的元。∀x0∈E定义Ishikawa迭代序列：

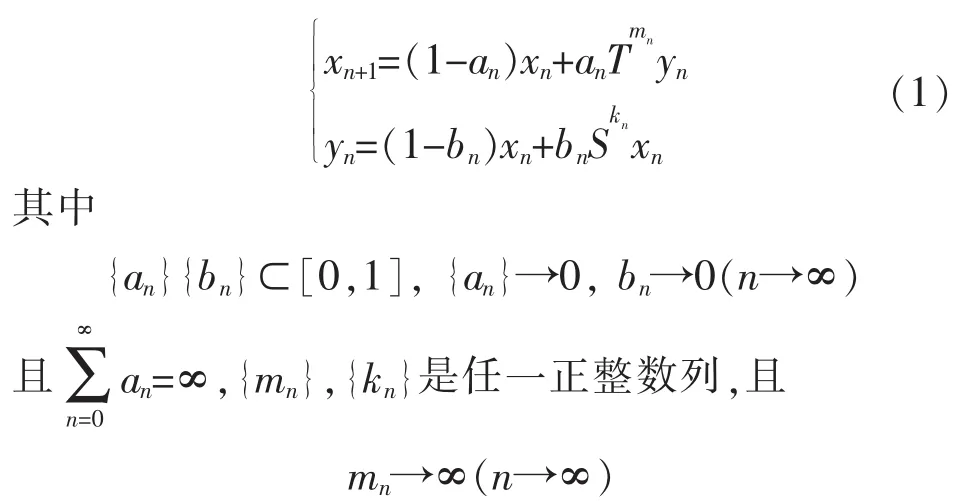
则由迭代产生的｛xn｝强收敛于q。

证明 由引理1及式（1）

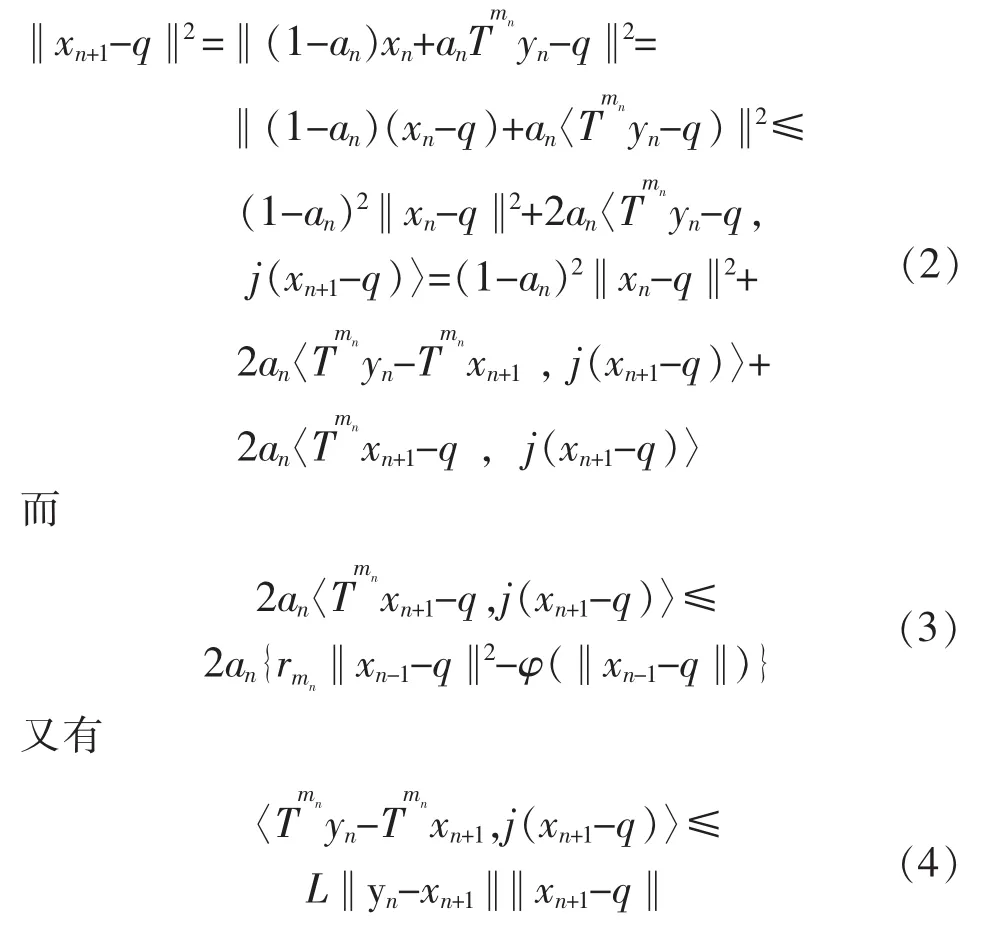
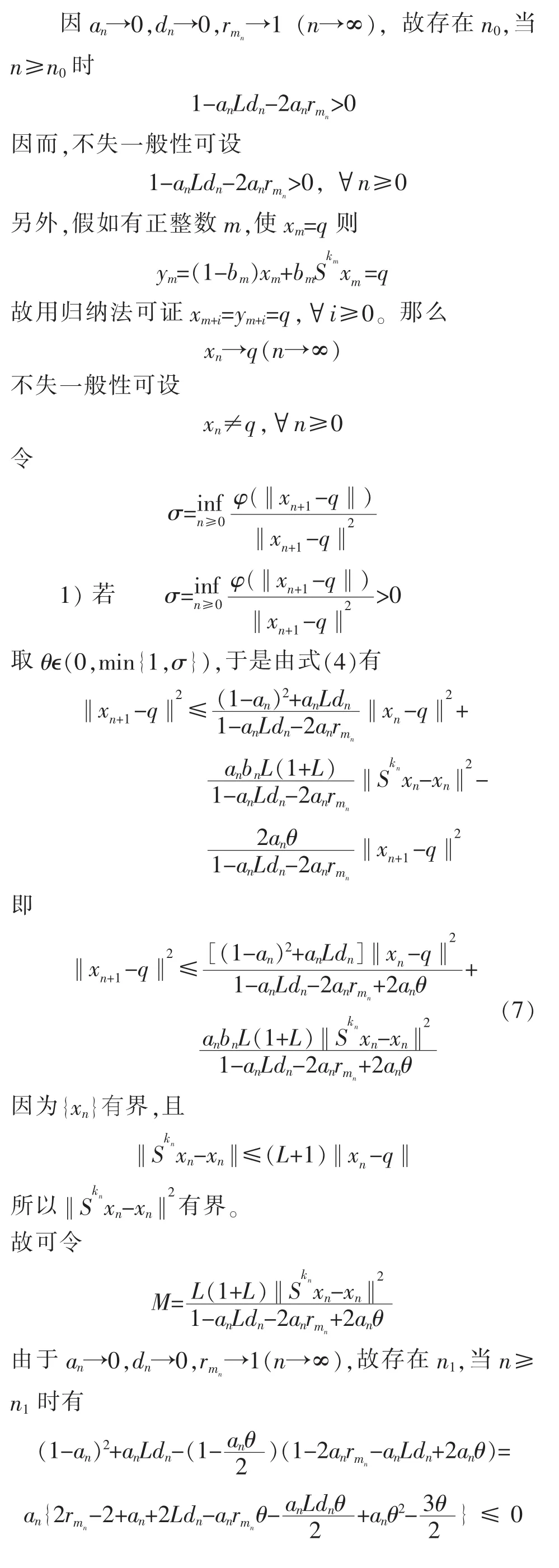
这与式（10）矛盾。故

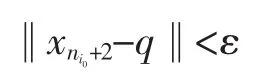
根据归纳法可知式（9）成立。又由ε的任意性可得

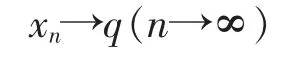
［1］Goebel K,kirk W A.A fixed point theorem for asymptotically nonexpansive mappings［J］.Pro Amer Math Soc，1972，35（1）:171-174.

［2］Schu，Iterative construction of fixed points of asymptotically nonexpansive mappings［J］.J.Math.Anal. Appl，1991，158:407-413.

［3］N.Shahzad.Approximating fixed points of nonexpansive mappings in Banach spaces［J］.Nonlinear Anal,2005（61）：1031-1039.

［4］J.S.Jung.Iterative approaches to common fixed points of nonexpansive mappings in Banach spaces［J］.J.Math. Anal.Appl，2005，302：509-520.

［5］陈汝栋，姚永红.一致-伪压缩映象不动点的迭代逼近［J］，应用泛函分析学报，2004，6（1）：93-96.

［6］姚永红,陈汝栋.渐近伪压缩和渐近非扩张映象不动点的迭代逼近问题 ［J］.应用泛函分析学报，2007，9（3）：233-237.

［7］Chang S S.On Chidume’s open questions and approximate solutionsofmultivalued strongly accretive mappings equations in Banach spaces［J］.J Math Anal Appl,1997,216：94-111.

［8］Liu L S.Ishikawa and Mann iterative processes with errors for nonlinear strongly accretive Mappings in Banach spaces［J］.J Math Anal Appl,1995，194：114-125.

Iterative Approximation to a Common Fixed Point of Uniformly L-Lipschitzian Mapping Pairing

Li Wanji
（School of Sciences,Hubei University of Automotive Technology,Shiyan 442002,China）

The iterative approximation problem of fixed points for nonlinear operators in Banach spaces is one of the most important problems in the nonlinear approximation theory.Mann and Ishikawa iterative methods were generally used for finding fixed points of nonlinear operators.The iterative approximation to a common fixed point of uniformly L-Lipschitzian mapping pairing in Banach spaces was discussed.Some corresponding results of references［5－6］were improved,extended and developed.

asymptotically nonexpansive mapping;asymptotically pseudo-contractive mapping; Ishikawa iteration;fixed point

O29

A

1008－5483（2014）01－0067－04

2013-11-21

李万继（1983-），男，湖北十堰人，硕士生，主要从事不动点理论及应用研究。

10.3969/j.issn.1008-5483.2014.01.0017