关于条件分布及其应用的教学研究

吕文华，韩慧霞

概率统计是高校理工科专业学生的一门基础课程，而条件分布是概率论中一个重要的概念，是研究变量之间相依关系的一个有力工具，在工程计算、金融保险等领域都有广泛的应用，也是教学的一个难点。因此，如何使学生深刻理解条件数学分布的概念、熟练掌握其计算方法是概率统计教学的一个重要问题。

1 由简单实例引入对问题的探讨

在条件分布的教学中，常通过对一个简单例子的分析指出条件分布的重要性，并使学生明确在已知Y＝y的条件下，X的条件分布与X的无条件分布是不同的。

例1 考虑一大群人，从其中随机抽取一个，分别以X和Y记其身高和体重，则X和Y都是随机变量，各自都有一定的概率分布。如限制1.8≤X≤1.9，在此条件下去求体重Y的条件分布，这就意味着从这一大群人中，把身高在1.8米和1.9米之间的人挑出来，然后在挑出的人群中求其体重的分布。由于身高和体重会有一定的正相依关系，这个分布与不设这个条件时的分布会很不一样。所以有必要研究把一个变量限制在一定条件下另一个随机变量的条件分布。

2 条件分布列与条件密度函数的计算公式

由于离散型随机变量常用分布列表示其分布，而连续型常用其密度函数，所以我们分别考虑条件分布列与条件分布函数。设（X，Y）为一个二维离散型随机向量，联合分布列为P（X＝xi，Y＝yj）＝pij，i，j＝1，2，…，考虑Y＝yj的条件下X的条件分布，即是要找条件概率P（X＝xi｜Y＝yj）由条件概率的定义，可得若P（Y＝yj）＞0，则

此即为在给定Y＝yj的条件下X的条件分布列。

为加深学生对概念的理解，应进一步补充说明，在Y＝yj条件不变的情况下，条件分布列仍是分布列，即满足：

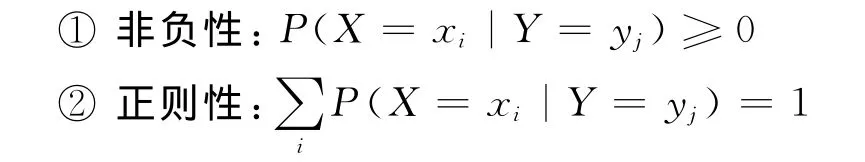
在连续场合中，因对任意y，P（Y＝y）＝0，故P（X＝xi｜Y＝yj）没有意义，首先考虑Y＝y时X的条件分布函数的概念.设二维连续随机变量（X，Y）的联合分布函数和密度函数分别为F（x，y），p（x，y），边际密度函数为pX（x），pY（y），则Y＝y时X的条件分布函数可以写成

分子分母各除以h，并分别取极限，则上式化为

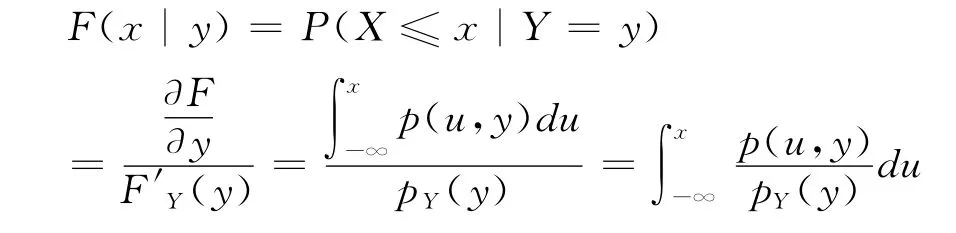
上式表明条件分布也是连续分布，并且在pY（y）＞0时，给定Y＝y条件下X的条件密度函数为

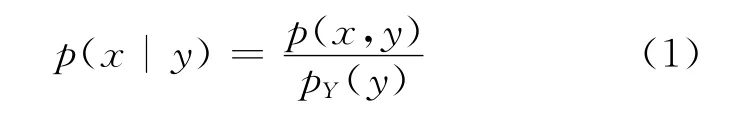
为加深学生对条件密度的理解，应强调两点：

1.条件密度函数仍然是概率密度，即满足概率密度的两点基本性质。2.（1）式可改写为：

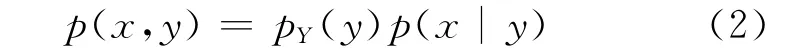
类似可得，

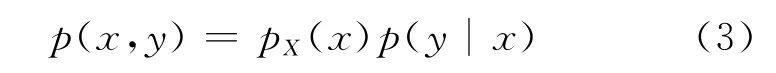
即两个随机变量的联合密度等于其中之一的概率密度乘以在给定这一个之下另一个的条件概率密度，这个公式与条件概率的公式P（AB）＝P（B）P（A／B）类似 。

3 条件概率分布在计算条件期望中的应用

由于条件分布列仍是分布列，条件密度函数仍然是条件概率密度，所以在此基础上可以求条件期望。其计算公式如下，若（X，Y）为二维离散型，

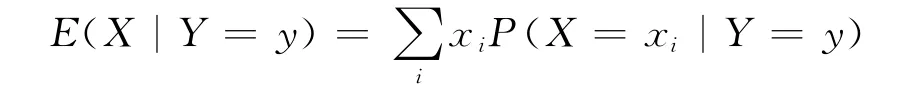
若（X，Y）为二维离散型，

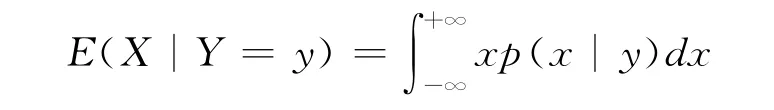
条件期望E（X｜Y＝y）是y的函数，它与无条件期望E（X）是有区别的。进一步指出若以E（X｜Y）记Y的如下函数：当Y＝y时它取值E（X｜Y＝y），这样定义的E（X｜Y）是一个随机变量，对它求期望可得有趣的结果。

例2 （重期望公式）设（X，Y）是二维随机变量，且E（X）存在，则

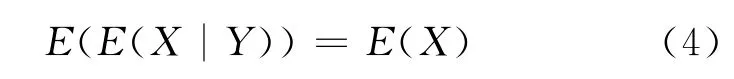
证：在此仅对连续场合给出证明，而离散场合可类似证明。设（X，Y）有联合密度p（x，y），

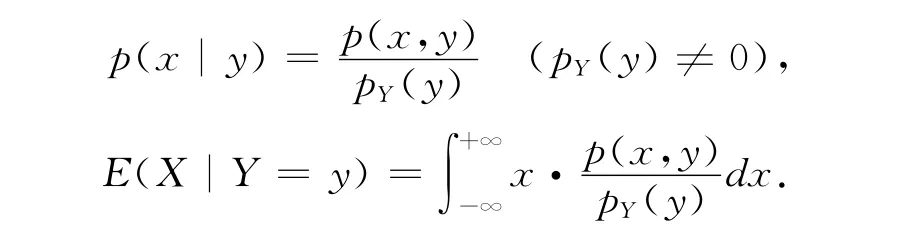
由Y的函数的期望公式，有

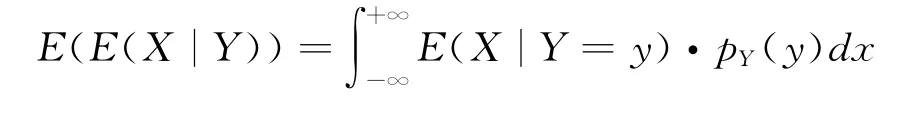
重期望公式是概率论中较为深刻的结果，它在实际中很有用.譬如，要求在一个取值于很大范围上的指标X的均值E（X），会遇到计算上的许多困难.为此可换一种思维方式：寻求一个与X有关的量Y，以Y的不同取值把大范围划分成若干个小区域，先在小区域上求X的平均，再对此类平均求加权平均，即可得到大范围上X的平均E（X）.

例3 一个矿工被困在有两个门的矿井里，第一个门通一坑道，沿此坑道走3小时可到达安全区；第二个门通一坑道，沿此坑道5小时又回到原处。假定此矿工总是等可能地在两个门中选择一个，试求他平均要用多少时间才能到达安全区。

解：设该矿工需要X小时到达安全区，Y表示第一次所选的门。

由题设条件知，

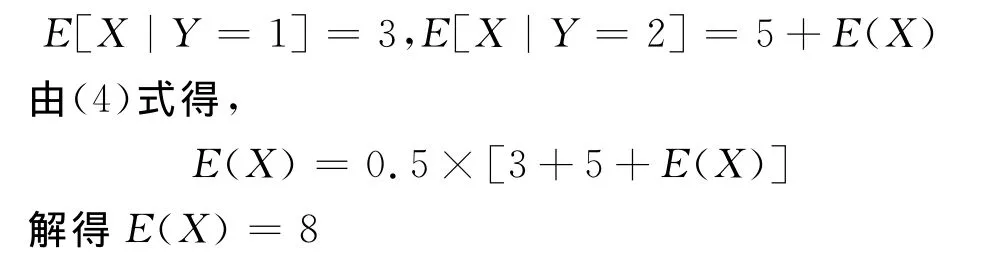
例4 （随机个随机变量之和的期望）设X1，X2，…为一列独立同分布的随机变量，随机变量N只取正整数值，且N与｛Xn｝独立，则有

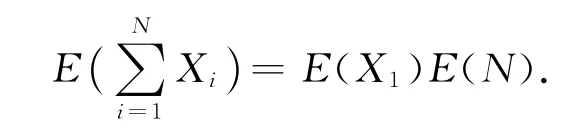
对此例子不要求学生掌握其证明，而是强调其在实际中的应用。如设一天内到达商场的顾客数N是仅取非负整数值的随机变量，且E（N）＝35000.又设进入此商场的第i个顾客的购物金额为Xi，可以认为诸Xi是独立同分布的随机变量，且E（Xi）＝82（元）.假设N与Xi相互独立是合理的，则此商场一天的平均营业额为

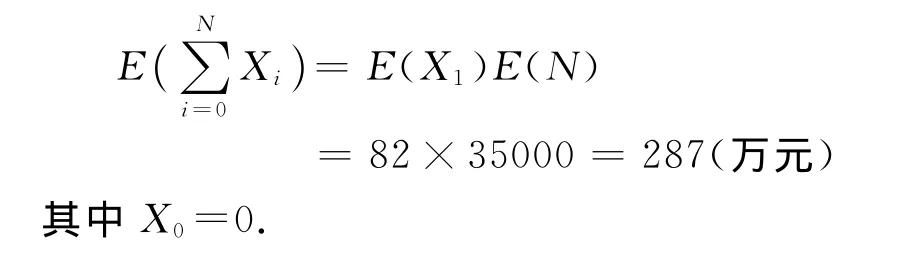
4 条件概率分布与随机变量的独立性

仅考虑（X，Y）为连续型，一般p（x｜y）随y的变化而变化，这反映了X与Y有相依关系，如果p（x｜y）不依赖于y，只是x的函数，由（1）式易得，p（x｜y）＝pX（x），则表示X的分布情况与Y的取值完全无关，这时就称X与Y这两个随机变量独立。

定义：设二维随机向量（X，Y）的联合密度函数为p（x，y），X与Y的边际密度分别为pX（x），pY（y），如果

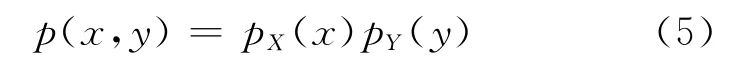
则称X与Y相互独立。

进一步解释之所以没有采用p（x｜y）＝pX（x）来定义X与Y的独立性，原因有如下两点

（1）式（5）总是有意义的，而用条件密度去定义时，可能碰到在个别点无法定义的情况，而在一般情况下可以用p（x｜y）＝pX（x）来验证其独立性。

（2）式（5）式在形式上关于两个变量对称，便于推广到对多个变量定义独立性。

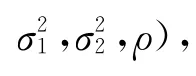
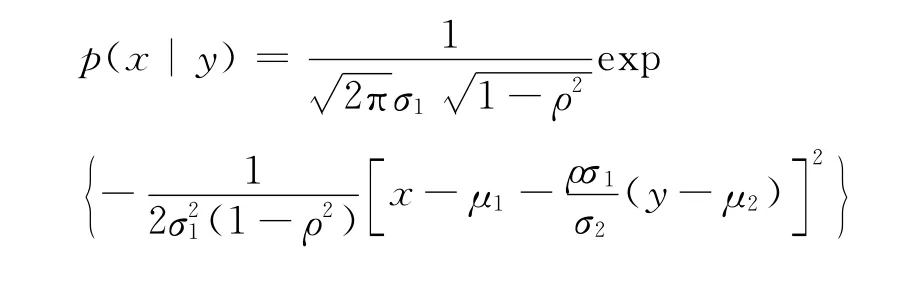
证：由二维正态分布的密度形式可得，从而 当且仅当ρ＝0时，p（x｜y）＝pX（x），即X与Y独立。

随着我国的高等教育由“精英型教育”向“大众化教育”转变，像我校这样的应用型本科院校，学生数学基础知识不够扎实，学习的主动性不足，以上教学方法在做法上淡化理论证明，强调对知识的应用。目的是使学生对概率统计这门课程感兴趣、克服畏难心理，对条件分布理论有一个较系统的把握。

［1］茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京：高等教育出版社，2010.

［2］陈希孺.概率论与数理统计［M］.合肥：中国科学技术大学出版社，2002.

［3］徐洪香.概率论的缘起、发展及其应用［J］.辽宁工学院学报，2001，21（3）：62－63.

［4］张克军.关于条件概率及其应用的教学研究［J］.徐州教育学院学报，2008，23（3）：134－135.

［5］沙秀艳，辛 杰.概率论与数理统计教学实践与探索［J］.大学数学，2013，29（4）：9－12.