基于S变换的电能质量扰动识别

王海元，李开成，张献

(1． 国网湖南省电力公司电力科学研究院，湖南 长沙410007;2． 强电磁工程与新技术国家重点实验室(华中科技大学)，湖北 武汉430074)

1 引言

随着电力工业迅猛发展，各种大功率电力电子设备以及敏感负荷的投入使用，产生了大量诸如谐波、闪变、电压骤升、电压骤降等电能质量扰动事件，对电网造成了污染，也严重影响了电网中其它负荷设备的正常运行，造成巨大的经济损失。对各种电能质量扰动进行治理，前提是能够找到合适的方法对扰动事件进行正确辨识与分类。

近些年来，国内外学者在电能质量辨识方面做了大量工作，电能质量扰动辨识的一般流程为，将信号经过时频分析工具得到信号的时频信息，然后从中提取出能够表征信号特征的一些时频量，经由分类器可得到分类结果。

提取特征量的时频分析工具很多，比较公认的有短时傅里叶变换〔1〕，小波变换〔2〕，S 变换〔3〕等等。短时傅里叶变换在传统的傅里叶变换的基础上加时间窗，将时间窗内的非平稳信号近似为平稳信号的方法，运用到非平稳信号的处理上取得了一定的效果，但是这些窗函数与频率f 无关，窗函数一旦确定，其在整个时频面上的窗口形状和宽度便确定了，即时间分辨率和频率分辨率不能改变，它只适合分析特征尺度大体相同的过程，不适合提取非平稳信号，如电压骤升、骤降、凹陷等信号的时频信息，因此不适合于非平稳信号的辨识。小波变换虽然对信号可以进行多尺度分析，变换尺度与频率的关系固定，不能提取任意频次的信号，而且小波系数受噪声的影响大，对于谐波或含噪声类扰动信号不能定量地提取扰动信号的幅值特征，因而也不适用于电能质量扰动分类的特征提取。S 变换是近些年来迅速发展起来的一种时频分析方法，它是短时傅里叶变换和小波变换的延伸，其引入了与频率成反比的高斯窗，突破了小波变换中高斯窗仅能在固定时间位置进行伸缩的限制，能够在时间轴上平移，具有与频率相关的分辨率，非常适合于电能质量扰动事件的特征提取。

从近些年的发展来看，用得较多的分类器有神经网络〔4〕，模糊逻辑〔5〕，专家系统〔6〕和支持向量机〔7－8〕等。神经网络具有结构简单，求解问题能力强的特点，可以较好地处理信噪比低的数据，但是自身的不足也很明显，如存在局部最优、收敛性较差、训练耗时，容易过拟合，可靠性不高等问题。模糊逻辑算法简单，采用简单的if－then 形式的逻辑语句进行判断，对区别性较强的信号有着很高的辨识率，但是对于复合型的电能质量扰动，很难建立明显的if－then 规则。专家系统通过建立知识规则的形式来形成知识库，易于调试和理解，知识库易于维护和扩展，但是它不具备学习能力，容错能力差，伴随扰动种类的增多，专家系统会变得很复杂，容易产生组合爆炸的问题，而且可移植性差。

文中采用基于S 变换进行特征提取，通过S 变换对信号做时频分析，从S 变换得到的时频矩阵中，提取某些行和列，进行相关运算，得到特定的特征量，用SVM 进行分类。该方法只用到了4 个特征量，能够识别一些常见的，如电压骤升、电压骤降、谐波、电压骤升加谐波等8 种电能质量扰动，有分类速度快，辨识率高，而且在低信噪比的情况下仍有较高的辨识率等特点。

2 原理介绍

S 变换是由Stockwell 等学者于1996 首次提出的，作为短时傅里叶变换和小波变换的一种扩展，S 变换引起了学者的兴趣，正逐渐应用于电能质量扰动的时频分析中，成为了进行电能质量扰动特征量检测和模式识别的一种有效手段。

信号u(t)的连续S 变换S(τ，f)表示如下:

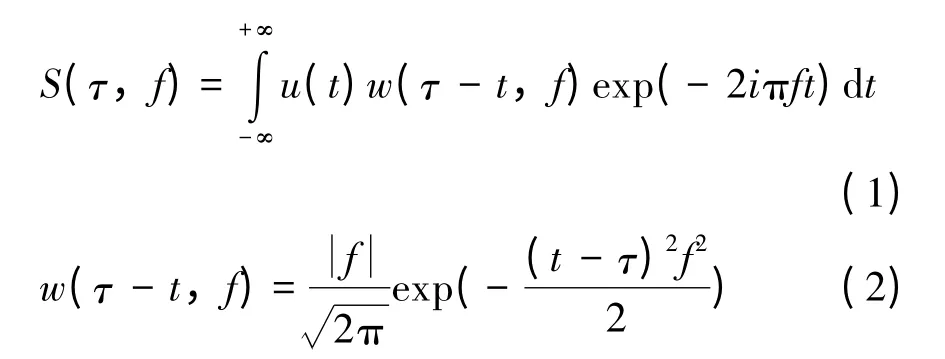
其中，w(τ － t，f)为高斯窗口，τ 为控制高斯窗口在时间轴位置的参数。从式(1)中可以看出，S 变换与短时傅立叶变换的不同之处在于高斯窗口的高度和宽度随频率而变化，这样就克服了短时傅立叶变换窗高和窗宽固定的缺陷。高斯窗在时间和频率上对称，高斯函数的傅里叶变换仍是高斯函数，使得信号u(t)可以由其S 变换进行重构，具有可逆性，S 逆变换的定义式为:

信号u(t)的S 变换与其傅里叶变换U(f)之间存在如下关系:

因此S 变换能通过快速傅里叶变换实现快速计算〔9〕。

S 变换还可以被认为是对小波变换的相位修正，并且可以从连续小波变换推导出来。信号u(t)的连续小波变换如下:

其中，τ 和d 分别为时移因子和伸缩因子，伸缩因子d 为频率f 的倒数，w(t － τ，d)为母小波的时移伸缩变换，若选取变换核为一高斯窗和一复向量的乘积，即:

那么，信号u(t)的S 变换可以表示为:

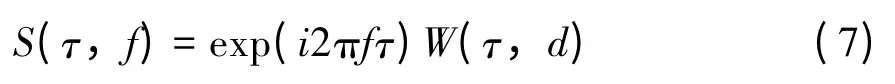
S 变换作为短时傅里叶变换和小波变换的一种扩展，用于信号分析有良好的时频特性，对信号进行S 变换得到的二维矩阵，其列对应采样时间点，行对应频率值，矩阵元素为对应的幅值，通过观察分析对应的行向量和列向量可以得到信号在具体时间点和频率点所对应的时频信息。图1 为一个标准信号及经过S 变换后的相关曲线，可以看出，通过找出合适的时频分量能够得到信号相关的时频信息。

图1 标准信号及S 变换相关曲线

3 基于S 变换和时域分析的特征提取

文中考虑的电能质量扰动事件有:电压骤升，电压骤降，电压中断，电压振荡，电压缺口，谐波，谐波加骤升，谐波加骤降。各信号的模型如表1 所示〔10〕，表中u(·)，sgn(·)分别为单位阶跃函数和符号函数。

文中以matlab 7.6 为仿真平台，信号的采样率fs=5 000 Hz，时长为10 个周期进行分析，主要考虑15 次及以下谐波，对标准信号以及8 中扰动信号进行S 变换分析。

表1 电能质量扰动数学模型

3.1 标准信号的S 变换分析

标准信号经S 变换以后，得到了一个二维的时频矩阵，图1 中，(a)为标准信号曲线，(b)为其频谱，在频率为50 Hz 处幅值为1 p.u.，所以(b)可以清晰反映信号的频谱。(c)为S 变换后二维矩阵中，幅值最大值所对应的时间序列，可以清晰反映基波分量幅值与时间的关系。

3.2 扰动信号的S 变换分析

图2 到图9 为8 种扰动事件的S 变换相关曲线，其中为了信号的分析方便，图5 到图7 为时频三维图，描述了在具体时间频率点下对应的幅值。其余几个图中每个图的物理含义与图1 所对应一致。

图2 电压骤升的S 变换相关曲线

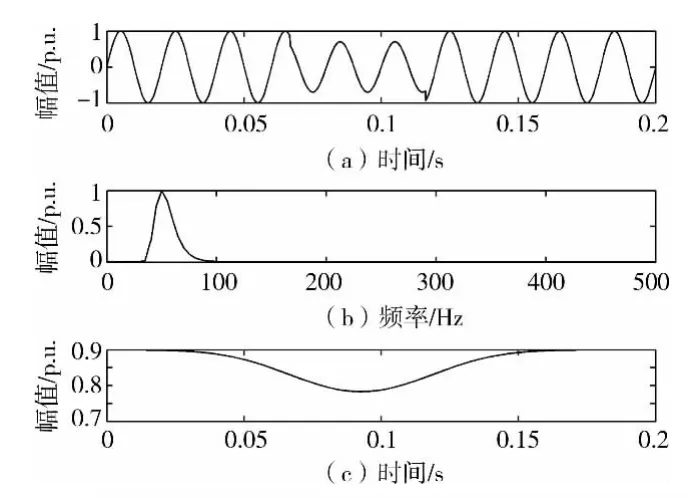
图3 电压骤降的S 变换相关曲线

图4 电压中断的S 变换相关曲线

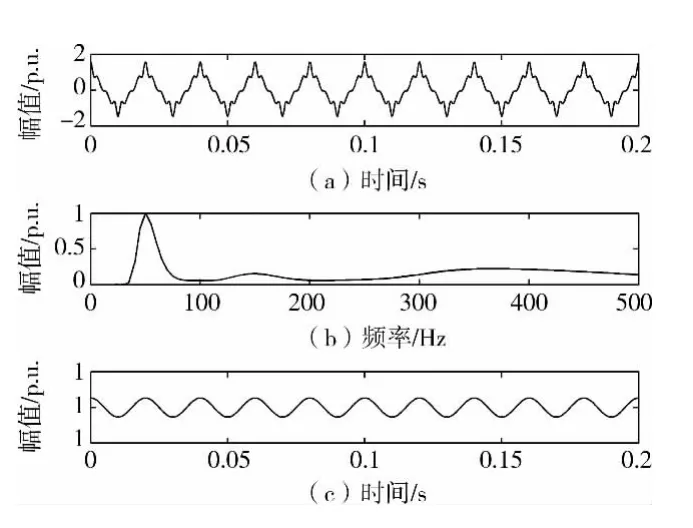
图5 谐波的S 变换相关曲线

图6 暂态振荡的S 变换相关曲线

图7 电压缺口的S 变换相关曲线

图8 谐波+电压骤升的S 变换相关曲线

图9 谐波+电压骤降的S 变换相关曲线

3.3 基于S 变换的特征提取

通过定义如下4 个参数，可实现对电能质量扰动事件的特征进行提取。

1)S1:基波幅值

求取基波幅值中的最值点p，取最值点前后各1/4 个周期的点求平均值:

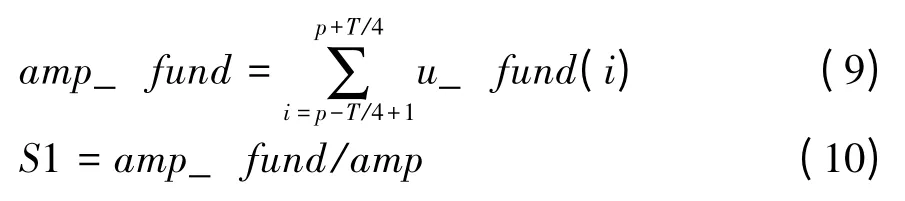
其中，amp 为信号的基波有效值，对于含有电压骤升的信号，1.1≤S1≤1.8;对于含有电压骤降的信号，0.1≤S1≤0.9;对于含有电压中断的信号S1＜0.1。

2)S2:低频段标准差

标准差用于判断一个状态序列中各数据偏离平均数的距离的平均数，对于基波幅值没有变化的信号，标准差趋近于0，而对于电压骤升，骤降，中断这类引起基波幅值在某段时间内有大的变化的暂态扰动事件，其基波标准差相对有比较大的值，因此，求出低频段各次谐波分量的标准差，如果基波标准差在这个标准差序列中有最大值，则认为发生了引起基波幅值有较大变化的暂态扰动事件。有最大值则S2=1;无则S2=0;

3)S3:谐波分量数

找出S 变换矩阵中幅值最大的频率曲线，寻找频率曲线中15 次谐波以下(即f＜750 Hz)的峰值数，如果信号中仅含有基波分量，则峰值数为1，如果信号中含有谐波分量，则峰值数大于1;

4)S4:高次谐波标准差

高次谐波标准差用来区分电压缺口和暂态振荡，在高次谐波段，暂态振荡仅在某个时间段含有高次谐波，而电压缺口的高次谐波基本上是均匀分布在整个时间轴上，因此对高次谐波段做标准差，暂态振荡会有一个较大的标准差，而电压缺口的标准差趋近于零。有最大值则S4=1;无则S4=0;

扰动信号分类与特征参数间的关系如表2。

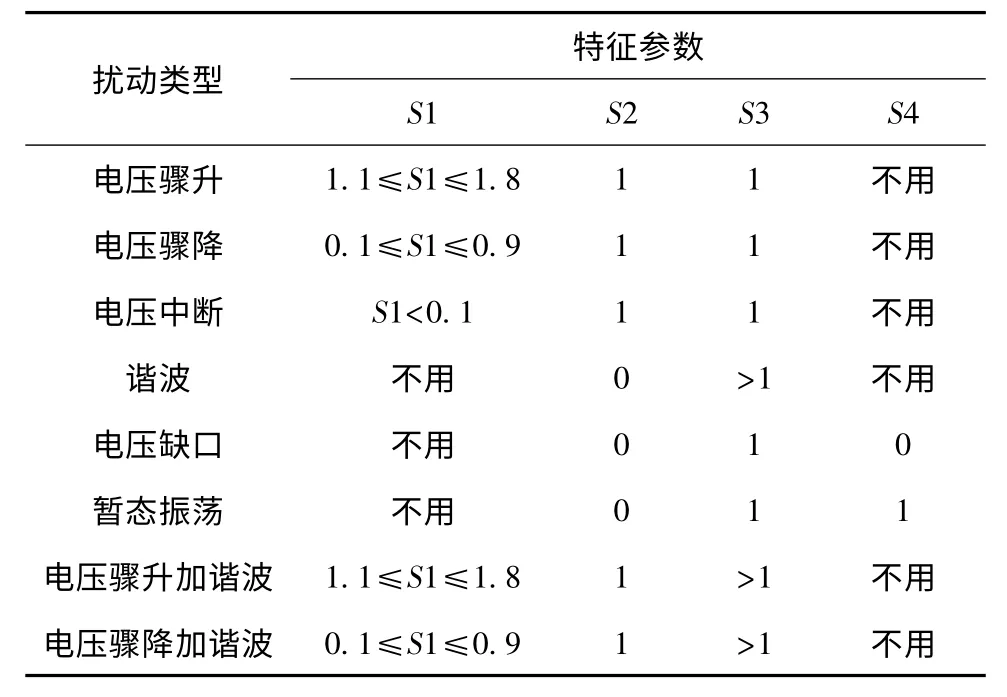
表2 扰动信号与特征参数的关系

3.4 使用SVM 对扰动事件分类

SVM 是一种典型的二分类器，它只能分辨样本是属于正类或负类这种问题。文中对8 种扰动事件进行分类，是多类样本的分类问题，可以将它们规定为［1，2，3，4，5，6，7，8］，以每个阿拉伯数字对应一个样本，在使用SVM 对8 种时间进行分类时，文中采用一对多组合(one against all)，原理是提取一类样本作为正类样本，其余数据作为负类样本，与本仿真对应就是，如将电压骤升事件标识为1，其余7 种事件标识为2，然后经过编码，将［1，2］编码为［－1，1］进行分类训练，训练结束后又将［－1，1］解码为［1，2］，这样便实现了对电压骤升事件与其余事件的分类，将电压骤升事件从8 种事件中分类出来。剩下的7 种事件，将电压骤降事件标识为2，其余6 种事件标识为3，然后经过编码，将［2，3］编码为［－1，1］进行分类训练，训练结束后又将［－1，1］解码为［2，3］，电压骤降便从7 种事件中分类出来，剩余的6 种事件按照如此一对多组合的方法，可以一次分类出来，这样，使用7 个SVM 分类器便可对8类扰动事件进行分类。

4 仿真分析

文中采用MATLAB7.6 作为仿真平台，对信号进行S 变换后提取上述特征量，然后使用7 个SVM 分类器对8 种扰动事件进行分类，考虑和分析了信号无噪声，以及分别含有50 dB，40 dB，30 dB，20 dB 噪声几种情况下的分类结果。每类事件样本100 个，对每类事件的分类辨识率以及总辨识率以表格形式做出了相关统计，如表3 所示。

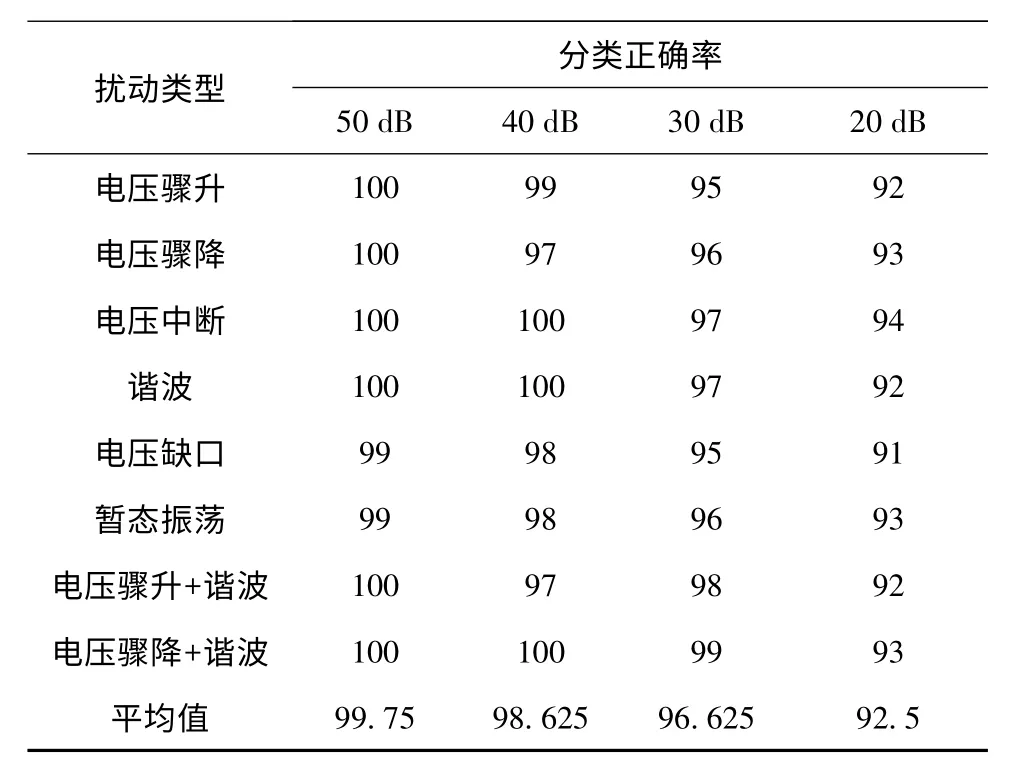
表3 扰动辨识的仿真测试结果 %

由表3 的仿真结果可知，在大的信噪比下，分类辨识率高，随着信噪比的降低，辨识率也随之下降。但是总体来说，不论是对于单个事件的辨识还是整体的辨识，在不同的信噪比下，文中采用的S变换+动态测度法提取特征量的扰动自动辨识系统均有很高的辨识率。

5 结论

文中采用S 变换的特征提取方法，能够对6 种单一的电能质量扰动事件和2 种复合的电能质量扰动事件进行辨识。用SVM 对扰动事件进行分类，易于添加新的特征量来识别新引入的扰动模型，同时还可省去人工智能的训练过程以及因样本数不足而导致的较大辨识误差。采用文中的方法对扰动事件进行辨识，辨识率高，且具有较强的抗噪性，在电能质量的自动辨识中具有较大的应用前景。

〔1〕赵凤展，杨仁刚． 基于短时傅里叶变换的电压暂降扰动检测〔J〕． 中国电机工程学报，2007，27(10):28-34，109．

〔2〕胡 铭，陈 珩． 基于小波变换模极大值的电能质量扰动检测与定位〔J〕． 电网技术，2001，25(3):12-16．

〔3〕Dash P.K，Panigrahi B.K，Panda G． Power quality analysis using S-transform〔J〕． IEEE Trans on Power Delivery，2003，18(2):406-411．

〔4〕Zwe－Lee G． Wavelet-based neural network for power disturbance recognition and classification〔J〕． IEEE Trans on Power Delivery，2004，19(4):1 560-1 568．

〔5〕程其云，孙才新，张晓星，等． 以神经网络与模糊逻辑互补的电力系统短期负荷预测模型及方法〔J〕． 电工技术学报，2004，19(10):53-58．

〔6〕杨洪耕，刘守亮，肖先勇，等． 基于S 变换的电压凹陷分类专家系统〔J〕． 中国电机工程学报，2007，27(1):98-104．

〔7〕Peter G.V.Axelberg，Irene Yu － Hua Gu，Math H.J.Bollen．Support Vector Machine for Classification of Voltage Disturbances〔J〕． IEEE Trans on Power Delivery，2007，22(3):1 297-1 303．

〔8〕张学工． 关于统计学习理论与支持向量机〔J〕． 自动化学报，2000，26(1):32-42．

〔9〕易吉良，彭建春，谭会生． S 变换在电能质量扰动分析中的应用综述〔J〕． 电力系统保护与控制，2011，39(3):141-147．

〔10〕黄南天，徐殿国，刘晓胜． 基于S 变换与SVM 的电能质量复合扰动识别〔J〕． 电工技术学报，2011，26(10):23-30．