应用最大实体要求的位置度过程能力评价方法
张 爽,高金刚
(长春工程学院,长春 130012)
0 引言
在生产过程的质量分析与控制中,过程的概念越来越受到重视,过程能力与过程能力指数的研究越来越受到人们的关注。过程能力是指在生产过程处于稳定状态时,该过程所生产的产品能满足质量要求的能力。而过程能力指数则是将过程能力量化后的评价标准,表示过程能力满足质量技术要求的程度。
位置度是用以控制被测要素的位置要求,是零件上被测的点、线、面的实际位置偏离理想位置的程度。最大实体要求是当被测要素和基准要素偏离最大实体尺寸时,形位公差可以获得补偿值的一种公差原则。但是应用最大实体要求的位置度,由于当尺寸公差偏离最大实体尺寸时位置度公差可以补偿的原因导致位置度公差变化,而不能应用过程能力指数求值公式对过程能力进行评价。针对此问题,目前普遍方法是忽略最大实体要求进行过程能力评价。与形位公差相比,如果最大实体要求的补偿值很小,这时计算过程能力指数有效。但是如果应用最大实体要求的补偿值对公差的影响很大,即来自尺寸公差变化位置度公差获得的应用最大实体要求的补偿值与位置度公差值相比占到很大部分,忽略最大实体要求进行过程能力评价则会产生误判。
针对以上实际问题,本文以衬套为研究对象,提出一种的应用最大实体要求位置度过程能力评价方法,解决了因为应用最大实体要求位置度公差变化导致过程能力指数无法求出的问题。
1 基于最大实体原则的过程能力指数计算过程
1.1 过程能力指数简介
过程能力指数是英文Process Capability index的缩写,一般定义为技术要求与过程能力的比值。也就是说,过程能力指数越大,过程能力越能满足技术要求,产品质量越有保证,合格率越高。
过程能力指数(CPK) 计算公式为:

式中USL为规范上限, LSL为规范下限,m为过程的平均值,s为过程的标准差。
当规范为单侧下限时:
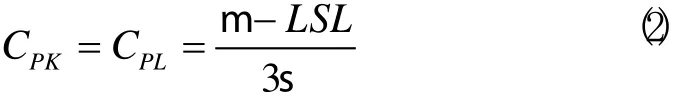
当规范为单侧上限时:
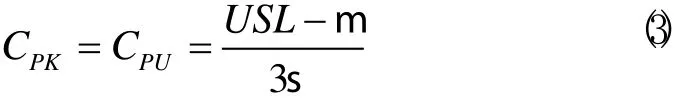
一般情况下, 无论是单侧规范限还是双侧规范限, 工艺规范值均有一个确定的数值要求。对于单侧公差, CPK可以应用标准公式来计算,公式中只需要已知公差值与所求过程的均值及标准差。但是应用最大实体要求时,位置度公差已经变为一个动态的变化值,这样对于计算PKC 是非常困难的。一种方法是忽略最大实体要求进行过程能力评价。与形位公差相比,如果最大实体要求的补偿值很小,这时计算过程能力指数有效。但是如果应用最大实体要求的补偿值对公差的影响很大,这时就需要使公差值统一。
1.2 研究对象
本文以图1所示衬套为研究对象。内径位置度公差为 0.2f mm,位置参考基准A为外圆柱的轴心,并且被测要素孔应用最大实体要求。

图1 衬套示意图
当孔处于最大实体状态时,即孔的实际尺寸处处皆为最大实体尺寸 8.0f mm时,孔位置度公差为 0.2f mm。当孔偏离最大实体状态,即孔径变大时,其孔径的变化值等于位置度补偿值。当孔处于最小实体状态时,即孔的实际尺寸处处皆为最小实体尺寸 8.1f mm时,位置度公差得到了最大的补偿值0.1mm。此时孔位置度公差变为 0.3f mm。根据实际中孔位置度公差值和孔径的实际尺寸的变化规律绘制出了动态公差图,如图2所示。
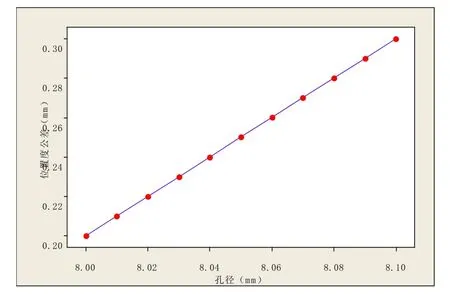
图2 动态公差表
由于应用最大实体要求,当孔处于最小实体状态时,位置度公差得到了最大的补偿值0.1mm。而忽略最大实体要求时,孔位置度公差为 0.2f mm,最大实体的要求的补偿值占到孔位置度的50%,所以不能采用忽略最大实体要求补偿值的方法。本文提出一种将位置度公差值统一成一个固定值的解决办法,即最小半径间隙法。
1.3 最小半径间隙法
针对应用最大实体要求的位置度,一般的检测方法是使用位置度检具检测。孔的位置度检具通常设计成位置度检测销的检测方法。将衬套孔插入检测销中,如果能顺利插入,则判定为位置度合格,如果不能插入,则判定为位置度不合格。此方法简单易行,但是无法得到用于评价过程能力的数据。可以使用三坐标测量机检测位置度,可以得到衬套孔的直径与相对基准A即外圆的位置,再通过数学建模的方法构建出理论位置度检测销。理论位置度检测销与实际衬套孔的最小半径间隙值就可以得出。此最小半径间隙由衬套孔位置度误差与孔径大小的综合误差决定。对于每一个测量的孔,此最小半径间隙的变化,则完全反映出孔位置度的变化。
为了建立合适的过程能力评价方法,需要制定最差接受状态或限定规格用于与过程能力相比较。在本文例中,限定的规格就是理论位置度检测销与实际衬套孔的最小半径间隙值为0。间隙值由孔径的变化值与孔轴心位置共同决定。见图3所示,此间隙值为单边公差,最小的接受条件是间隙值为0。由于孔径的值受到最大实体尺寸的约束,间隙值的最大接受条件不必定义。
图纸衬套孔的直径为 f 8 .000.1mm,应用了最大实体原则的位置度为 f 0 .2mm,则理论位置度检测销
设求得的某一衬套孔未获得最大实体原则补偿的位置度为P,直径为D。
则实测孔与理论位置检测销的最小半径间隙为:
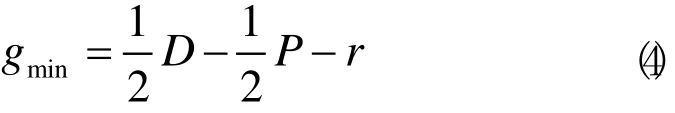
为了建立恰当的过程能力评价方法,现需要计算出过程能力最差接受条件或限制条件。在此例中,最差接受条件就是理论位置度检测销与实测孔之间的半径间隙为gmin=0。最小半径间隙如图3所示。

图3 最小半径间隙示意图
即应用最大实体原则的位置度PKC 值求值公式如下:
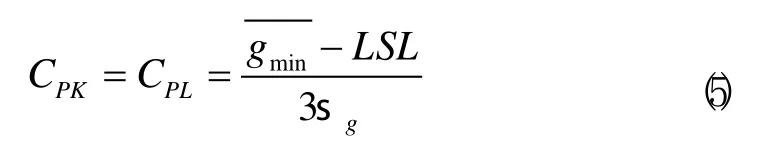

其中n为数据的数量, s g为最小半径间隙的标准差。
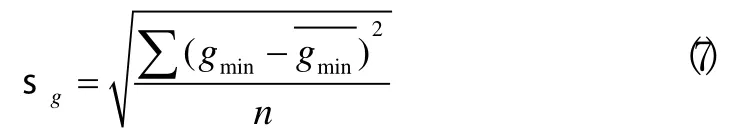
1.4 计算结果
对实际生产的衬套进行抽样,共计30件。应用三坐标测量机对此30件衬套位置度进行测量,需要注意的是该位置度值未获得最大实体原则补偿值。根据式5求得每个样品的最小半径间隙,如表1所示。

表1 三坐标测量结果与最小间隙数据
过程能力指数的计算的前提是数据是服从正态分布,所以应检查这30组数据是否服从正态分布。本文应用Minitab软件对此30个最小间隙数据做检验。应用Minitab作数据的正态性检验的方法有两种:正态性检验与图形化汇总。本文采用正态性检验法,并生成正态概率图,如图4所示。

图4 最小间隙正态性检验报告
生成正态概率图并完成假设检验验证图中的数据是否服从正态分布。对于正态性检验,原假设H0:数据服从正态分布;备择假设H1:数据不服从正太分布。图中纵坐标轴类似于正态概率纸的纵坐标轴。横坐标轴是线性标度尺。线段的作用是对数据的累积分布函数的估计。图中同时也展示了分布参数的数值估计:平均值与标准差, 正态性检验值及相关的P-value。
假设检验用于判断是否接受原假设。P-value是一个检验统计量,是实际计算极值的概率,临界值一般设定为0.05。如果P-value小于0.05,则拒绝原假设。图4正态性检验结果P-value为0.526>0.05,就基本可以认为数据正态,可以进行过程能力指数计算。则30个最小间隙数据服从正态分布,根据过程能力指数的计算条件,可以进行过程能力指数计算。使用Minitab软件计算结果见图5。从图5可知, CPK= CPL= 3 .49。则应用最大实体要求的孔位置度过程能力指数就等于最小半径间隙的过程能力指数,数值为3.49。

图5 过程能力分析报告
2 结论
本文应用概率统计和质量管理的理论,提出建立实测孔与理论位置度检测销之间的最小半径间隙分析模型和算法,解决了由于应用最大实体原则的位置度公差变化,无法计算位置度过程能力指数的问题。避免了复杂繁琐的数学运算。此方法重点强调形位公差的的理解,对形位公差过程能力评估较强的实际意义的工程应用。使用Minitab质量分析软件对实际案例分析计算出过程能力指数,实现对过程能力的评价。
[1] Graeme.Knowles, Guy March and Jiju Anthony,Evaluating Process Capability for Geometrically Toleranced Parts: A Practical Approach, Quality Engineering,14(3):365–374.2002.
[2] Geometrical tolerancing-Maximum material requirement,least material requirement and reciprocity requirement ISO 2692,1996.
[3] 田志友,田澎,王浣尘.非正态过程能力指数研究中的几个问题[J].工业工程.2005:29-32.
[4] 郭进利,赵彦云.新的过程能力指数[J].系统管理学报,2008,17(1):116-120.
[5] 宋祥彦.单侧公差及非对称公差过程能力指数[J].质量管理,2009(4):12-18.
[6] 盛家君,陈凯龙,周余庆.基于MINITAB的质量管理分析[J].2010:129-130.
[7] 韩亚利.基本过程能力指数的分析与应用问题研究[J].2012:185-187.
[8] 韩智敏.基于六西格玛的汽车备件物流质量控制研究[D].北京交通大学.2012.

