基于图论的计算机辅助装夹规划方法研究

许本胜，王 灿，黄美发

（1. 桂林航天工业学院 机械工程系，桂林 541004；2. 桂林电子科技大学 机电工程学院，桂林 541004）

0 引言

零件装夹规划是自动工艺规划的核心内容之一，其任务是通过综合考虑工件几何形状、尺寸和公差、加工资源等信息，来确定工件装夹的次数、顺序以及每次装夹中的定位基准、加工特征和加工方法[1]。

随着计算机技术的发展，如何利用计算机辅助进行零件的装夹规划已经受到人们的广泛关注和研究。如Zhang等[2]使用混合图理论对三轴立铣加工中心工件的装夹工艺进行设计。巢炎[3]等采用图论方法研究了零件加工自动定位设计的基本规则。张发平等[4]、黄伟军等[5]进行了面向CAPP的装夹规程数学建模和算法的研究。孙习武等[6]提出基于聚类分析法的装夹规划算法。当前研究虽然实现了一定程度上装夹规划的自动化，但主要采用的是基于经验的方法（如规则和知识库），且主要适用于只具有尺寸公差要求的情况。

几何尺寸和公差（Geometric Dimensioning and Tolerancing, GD&T）规范是当前加工制造业普遍采用的设计和制造标准规范。基准的概念和详细的形位公差方案是GD&T规范的特点，也是进行零件自动装夹规划的基础和条件。本文根据零件的GD&T规范，结合图论的表示方法，进行计算机辅助装夹规划方法的研究，具体包括装夹定位基准的确定、加工特征的聚类以及实现各组聚类特征之间的装夹排序三个基本方面的内容，目的在于为实现计算机辅助装夹规划提供基础。

1 GD&T规范及有向图表示

采用上下偏差来规定公称尺寸变动范围的参数化公差表示方法，是最早出现在零件图纸上的公差方案。由于没有指定明确的基准（如图1(a)所示），当零件的加工表面具有定向或定位要求时，这种仅采用上下极限偏差表示的公差方案含义是不明确的，给后续加工和检测阶段零件装夹方案的确定带来困难。相反，几何尺寸和公差方案以基准概念为基础，通过引入基准参考框架来确定零件各表面间的相对位置。如图1(b)所示，零件上A、B和C表面构成基准参考框架，通过基准面B和C可以明确指定孔的位置公差（包括形状和大小）。显然，几何尺寸和公差方案中，零件的尺寸、形状和几何特征的相对位置更为清晰和明确，为后续计算机辅助装夹规划带来了可操作性。

图1 两种公差方案比较

从几何和拓扑学角度看，零件功能表面可以划分为平面、圆柱面、球面等共7种类型。为了更好地表示零件各功能表面间的联系，Clement等提出了MGDE（minimum geometric datum elements）概念[7]，即最小几何基准要素，MGDE实质上是由参考点、参考线或参考面组成的最小集合以确定相应的功能表面不变。7种基本功能表面及最小几何基准要素为构成零件的基本几何特征，各基本几何特征之间的公差关系可利用图论的方法来描述，如图2所示。

图2 特征公差关系有向图表示

图2中，节点v1、v2和v3表示零件几何特征，联结各节点的边表示各加工特征之间的基准和公差关系。显然，由于两节点间的公差约束存在多个的情况，常规的有向图难以对其进行表示。为此，在常规有向图的基础上，通过增加对两个节点间约束关系的描述，采用扩展有向图进行零件几何特征-公差关系的表示，如下：

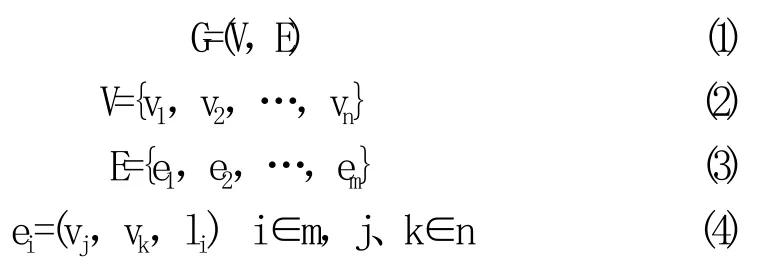
式中V为节点集合，元素vi(i=1，2，…，n，n为节点个数)为图的节点，vi代表零件上某个基准或加工表面；E为各节点间边的集合，元素ei为连接节点vj和vk的有向边，每条边表示两节点间的一种公差约束关系；li为对应边ei的属性，如公差类型、公差值等的描述。

2 基于图论的计算机辅助装夹规划

2.1 几何特征-公差关系有向图的计算机表示

有向图的计算机表示常见方法为邻接矩阵。采用矩阵进行图的存储时，矩阵的长度不能够动态变化，当图的顶点个数改变时需重写邻接矩阵，难以实现如顶点的增加和移除等有关图的操作，因而采用邻接矩阵的表示方法灵活性差。另外，采用矩阵的表示方法不能描述节点间存在多种关系（如两加工表面间存在多个公差约束）的情况。

为了方便装夹规划问题的计算机处理，本文采用面向对象的编程方法来实现扩展有向图的计算机表示，有关结构体和类的代码如下：

struct Label{ //边

int id;

CString name;

CString tolerance_type;

float tolerance_value;

}

struct Node{ //节点

int id;

CString name;

LinkList＜Label＞ formEdges; //LinkList＜Label＞边对应起始节点储存链表

LinkList＜Label＞ toEdges; // LinkList＜Label＞边指向节点储存链表

}

class Graph{ //图

private:

LinkList＜Node＞ nodes; // LinkList＜Label＞

为节点储存链表

public:

void add(Node); //增加节点

void remove(Node); //移除节点

void join(Node, Label, Node); //添加两节点间的公差约束关系

void getSubGraph(Graph g); //获取装夹子图

void unitGraph(Graph g1, Graph g2); //合并子图

void getSetup(); //装夹规划结果集

}

2.2 加工特征的聚类

所谓加工特征的聚类指的是根据几何特征-公差关系对各加工特征进行分组。对加工特征进行聚类时，首先需要确定装夹基准特征。装夹基准的计算机辅助确定方法可由几何特征-公差关系有向图中各节点的入度（指向节点的边的条数）来确定。入度为零的节点形成初始加工基准，如图3中节点X、Y和Z构成初始加工基准框架（X、Y、Z）。入度为3的节点，指向该节点的三条边构成装夹基准，如图3中指向节点A的三条边（X，A）、（Y，A）和（Z，A）以及指向节点B的三条边。

在进行加工特征的聚类时，必须遵循一定的规则，如：

图3 加工特征聚类示例

规则1：先前完成加工的几何表面特征优先作为装夹基准。

规则2：为减少加工误差的累积，一次装夹尽可能完成多个几何表面特征的加工。

通常零件需要多次装夹才能完成各几何表面特征的加工，进行装夹规划还必须考虑各装夹基准参考框架的加工生成顺序，对应有如下规则：

规则3：装夹规划次序必须根据装夹基准参考框架自身加工生成的顺序来安排。

根据几何特征-公差关系有向图，将图中节点分为三类：入度为零的节点、出度为零的节点和其他节点。其他节点的特点在于加工时不但具有装夹基准要求，同时在完成加工后有可能作为后续加工特征的装夹基准。由此，加工特征聚类的算法为：从图中出度为零的节点开始，根据边的指向关系，逆向追溯直至找到入度大于等于3的节点，且指向最终节点的三条边对应的起始节点为该组加工特征的装夹基准，并将这些节点归为一组。若逆向追溯的最终节点的入度大于3，则根据规则1，选择先前完成加工的三个节点作为该组加工特征的装夹基准。对于所获得的结果，根据规则2，可将具有相同的装夹基准的多组加工特征合并为一组；最后，由规则3，具有不同装夹基准的各组加工特征，根据装夹基准完成加工的先后来安排其装夹规划的次序。据此思路对图3所示加工特征进行聚类，得到各分组次序及装夹基准结果如表1所示。

表1 加工特征的聚类

2.3 算法流程

由以上分析，基于扩展有向图的计算机辅助装夹规划算法流程为：

1)根据零件图确定加工特征-公差关系有向图，并进行计算机存储和表示；

2)从出度为零的节点开始，根据边的指向，逆向追溯至入度大于等于3的节点，获取包括装夹基准特征在内的装夹子图，即实现对加工特征的聚类；

3)除初始基准特征（入度为零的节点）以外，判断其余各节点是否全部包含在步骤3的装夹子图结果中，若是则表明全部加工特征都已经实现装夹聚类，从而可以继续步骤4），否则从判断节点开始执行步骤2；

4)将具有相同装夹基准的多组加工特征合并为一组；

5)按照基准参考框架的加工生成顺序对各组加工特征进行排序，并输出最终装夹规划结果。

由于实际加工中，零件某些加工特征在加工后会作为其它特征的加工装夹基准，上述流程中的步骤3目的在于保证所有加工特征节点在各自的聚类分组中都实现加工，从而保证装夹规划的完整性。

与2.1节中有向图计算机表示相对应，步骤2、3结果由getSubGraph(Graph g)获得、步骤4由函数unitGraph(Graph g1, Graph g2)实现，通过执行函数getSetup()完成步骤5。

3 实例分析

以某简化汽车底盘前转向节零件为例，该零件是汽车制动系统、悬架系统和转向系统的接合关节。零件上各几何加工特征如图4所示。由零件功能确定的几何加工特征-公差关系有向图如图5所示。

图4 示例零件几何表面加工特征示意图

图5 加工特征-公差约束关系扩展有向图

按图5完成对加工特征-公差约束关系扩展有向图的计算机存储和表示。在此基础上，根据前述装夹规划算法流程，首先计算各节点出度和入度，得到入度为零的初始加工基准（X、Y、Z），其余特征为装夹规划中的待加工特征。从出度为零的节点C、E和G开始，向前追溯分别得到以下加工特征分组：

查询各分组中除基准特征以外的加工特征，可判断出没有对加工特征B进行装夹规划。因而从节点B开始继续向前追溯，得到聚类特征B←（X、Y、Z、A），由于特征X与A之间存在基准约束关系，特征X先于A加工，由规则1，优先选择特征X作为特征B的装夹基准。从而有加工特征分组：

结果（5）～（8）中，共有两组装夹基准，显然基准（X、Y、Z）先于（A、B、Z）加工生成。从而，按照规则2和规则3，对具有相同基准的各分组加工特征进行合并、装夹排序，得到最终装夹规划结果如下：

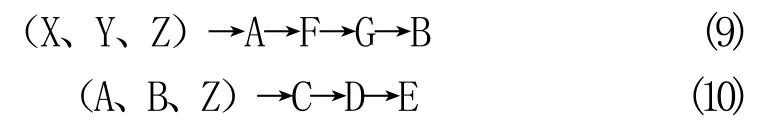
根据本文方法，采用VC6.0编程软件进行装夹规划原型系统的开发，示例零件结果如图6所示。

图6 原型系统

4 结论

本文从零件几何尺寸和公差规范着手，阐述了基于图论的计算机辅助装夹规划方法，包括零件加工特征-公差关系的扩展有向图表示、加工特征的聚类以及装夹规划的算法流程。实例表明，本文方法可以有效地确定工艺路线中的装夹次数、装夹基准和装夹顺序。后续将从以下两个方面对本文方法作进一步的完善：1）综合考虑加工资源，如机床加工能力、生产方案对装夹规划的影响，加强加工特征聚类和装夹顺序处理能力；2）实现零件在装夹、加工过程中的误差累积关系分析和建模，与夹具设计集成。

[1] Y.Zhang,W.Hu,Y.Rong, etc. Graph-based set-up planning and tolerance decomposition for computer-aided fixture design[J].International Journal of Production Research,39:14,3109-3126.

[2] ZHANG H C,LIN E.A hybrid-graph approach for automated setup planning in CAPP[J].Robotics and Compute-Integrated Manufacturing,1999,15(1):89-100.

[3] 巢炎,杨将新,吴昭同.基于图论的产品自动定位设计[J].浙江大学学报(工学版),2005,39(12):1925-1929.

[4] 张发平,孙厚芳,焦黎.面向CAPP的装夹规程模型与算法研究[J].北京理工大学学报,2006,26(12):1056-1060.

[5] 黄伟军,胡于进,蔡力钢.面向CAPP的零件装夹规划算法研究[J].中国机械工程,2011,22(22):2700-2706.

[6] 孙习武,褚学宁,苏於梁,汤岑书.基于聚类分析法的装夹规划算法研究[J].计算机集成制造系统,2009,15(6):1179-1186.

[7] Clement A.Riviere A.Tolerancing versus nominal modeling in next generation CAD/CAM system[A].In:Processing of 3rd CIRP Seminar on Computer Aided Toleracing, Cachan, France, 1993:98-113.